基于遗传算法的移动机器人路径规划

  之前在网上找基于遗传算法的移动机器人路径规划资料的时候，没有找到理想的开源代码。最后参照论文，用matlab写了代码。最近开了公众号——Joe学习笔记，会不定期更新一些文章，主要是自己平时学到的知识，内容包括自动驾驶、计算机视觉、人工智能和机器人技术。我会第一时间把文章更新在公众号上，感兴趣的可以扫描下面的二维码关注并分享哦！

　　最近新出了一个关于机器人路径规划和轨迹优化的视频课程，介绍常用的路径规划算法和轨迹优化算法，感兴趣的可以点击b站链接观看。更新中。。。 https://www.bilibili.com/video/BV1yT4y1T7Eb
　　遗传算法视频讲解地址：https://www.bilibili.com/video/BV1Sf4y1475E/

下面具体来讲讲基于遗传算法的移动机器人路径规划，文章是从公众号上搬过来的。
1.地图的建立和种群编码
　　机器人进行路径规划之前首先要建立地图，本文采用栅格法建立移动机器人的行走空间模型。栅格面积越小，空间中各种环境信息表示越精确，但同时占用的存储空间就会加大，算法所使用的搜索时间就会加大。若栅格面积越大，则空间中各种环境信息不能准确表示出来，容易出现碰撞问题。所以在建立环境模型时，需要先做以下规定：
（1）不考虑障碍物高度问题，机器人行走空间为二维平面空间；
（2）障碍物的大小、位置已知，并且不存在动态障碍物；
（3）在规划时可以把机器人看做质点处理。
　　为了方便设置栅格面积，我们通常用正方形表示机器人的行走空间。如果障碍物面积小于正方形面积，可以将障碍物扩大为正方形；如果障碍物面积大于正方形面积，可以用两个正方形表示障碍物面积；如果障碍物面积更大，则可以用多个正方形表示。建模后机器人行走空间如图1所示，图中白色部分为自由栅格，黑色部分为障碍物栅格。

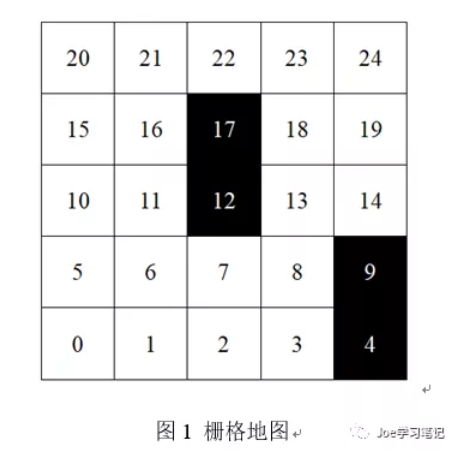
　　在构建栅格地图时，首先以地图左下角第一个栅格为坐标原点建立直角坐标系。因此每一个栅格可以用（x,y）的坐标形式表示，比如左下角第一个栅格可以表示为（1,1）。并且从左下角开始每一个栅格进行编号N，编号从0开始。编号和坐标的转换公式为：

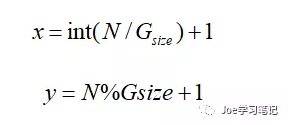
　　Gsize为每一行栅格数，int为取整操作。已为每一个栅格编好号码，因此可以用此编号来表示一条路径，比如起点为0终点为24的路径可以表示为（0，6，7，8，13，19，24），在遗传算法中即为十进制编码。
2.代码整体框架
　　遗传算法是一种智能优化算法，主要用来解决优化问题，其主要步骤为种群初始化、适应度函数计算、选择、交叉和变异。应用于移动机器人路径规划时其主要步骤相同，流程图如图2所示。具体每步的方法将在以下小节做详细介绍。

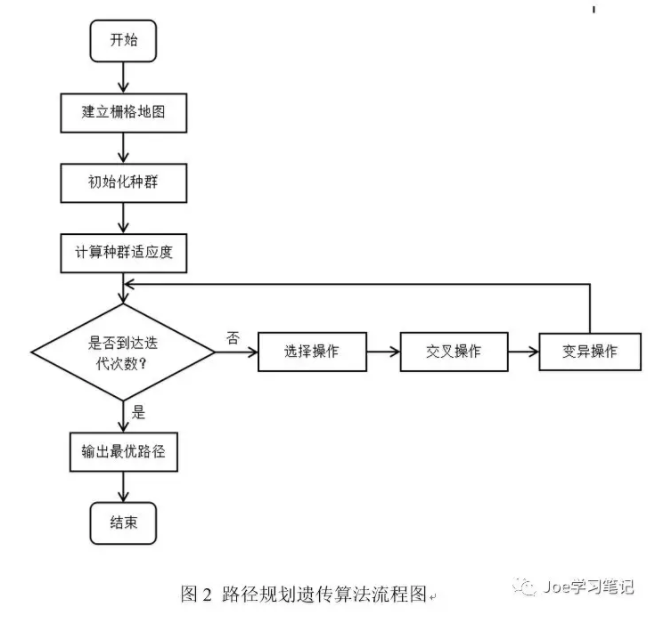
3.初始化种群
　　机器人的起始位置为栅格0，目标位置为栅格99。初始化种群要求随机产生多条可行路径，可行路径表示不与障碍物栅格相碰撞的路径。可行路径的产生分为两个主要步骤。第一步首先产生一条间断路径。机器人每次行走一个栅格，因此每一行至少有一个栅格在可行路径中。所以初始化时先按顺序在每一行随机取出一个无障碍栅格，形成一条间断的路径，其中为了减短路径长度路径的第一个和最后一个栅格分别为机器人的起始位置和目标位置。
　　第二步是将间断的路径连接为连续路径。在这一步中首先从第一个栅格开始判断相邻的两个栅格是否为连续栅格，栅格是否连续的判断方法为：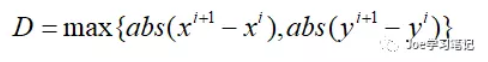
　　若D等于1则说明两个相邻栅格连续，反之不连续。对于不连续的栅格取两个栅格的中点栅格，中点栅格的坐标计算为：

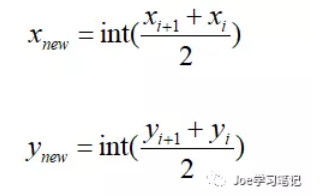
　　若新栅格为障碍物栅格则以上下左右顺序取新栅格的相邻栅格，并判断此栅格是否已经在路径中（防止陷入死循环），如果此栅格为无障碍栅格且不在路径中则插入路径中，如果遍历上下左右四个栅格后没有满足条件的栅格则删除这条路径；若新栅格为无障碍物栅格，则插入两个不连续栅格中间。继续判断新插入的栅格和新插入的栅格的前一个栅格是否连续，若不连续则循环以上步骤，直到两个栅格连续。当两个栅格连续后取下一个栅格，循环以上步骤，直到整条路径连续。初始化一条路径的流程图如图3所示。很久没画框图了把框图的开始和结束画成了长方形，懒得改了将就看下吧。

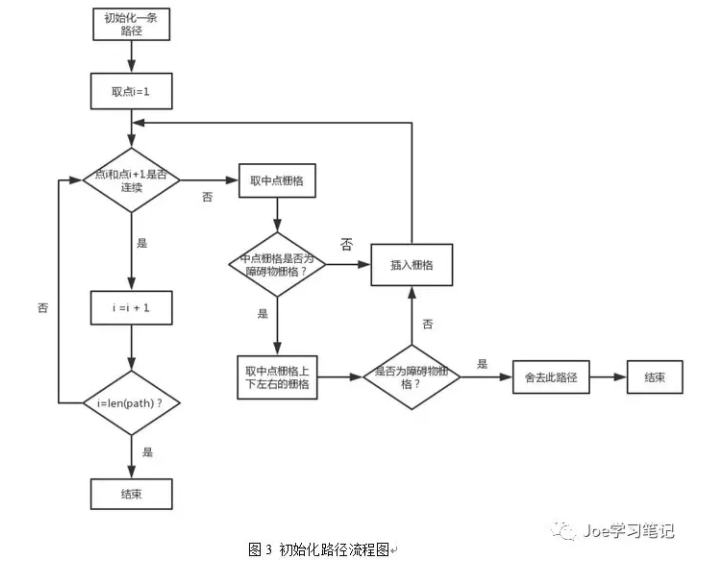
4.适应度函数计算
　　适应度函数分成两部分，分别用来判断路径的长短和平滑程度。路径长度的计算相对简单，公式如下：

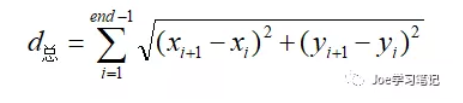
　　要求的是机器人的路径最短，而选择方式采用的是轮盘赌的方式，所以适应度函数的第一部分为：

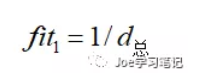
　　机器人由于运动学和动力学的约束，行进时拐弯不宜过大，并且相对平滑的路径有利于机器人的行驶，因此产生的路径有平滑度的要求。路径越平滑，相邻三点形成的角度越大，角度越大相邻三点之间的距离越大，因此计算路径中所有相邻三点的距离作为适应度函数的第二部分，计算公式如下：

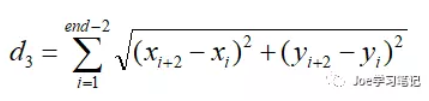
　　d3的值可对应路径中连续三点的夹角的四种情况分别为180度、钝角、直角和锐角，其中180度的三点成一直线，平滑度最好，钝角、直角次之。由于机器人动力学的约束，锐角是不允许的。所以分别对除直线外的3种情况给予惩罚，分别为5、30和无穷大，可以根据实际情况改动惩罚的大小。惩罚之和的倒数即为适应度函数的第二部分。
适应度函数的两部分需要取一个权重，权重公式如下：

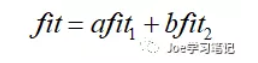
　　根据路径长度和平滑度之间的权重选择参数a和b。
5.选择方法
　　选择方法采用简单的基于概率的轮盘赌方法。首先计算出所有个体的适应度函数的和，再计算每一个个体所占的比率，计算公式如下：

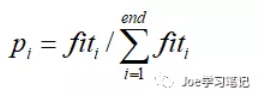
　　然后根据每个个体的概率，以轮盘赌的方式选择出下一代个体。轮盘赌的方式保证了部分非最优的个体，可以有效的防止算法陷入局部最优解。
6.交叉方式
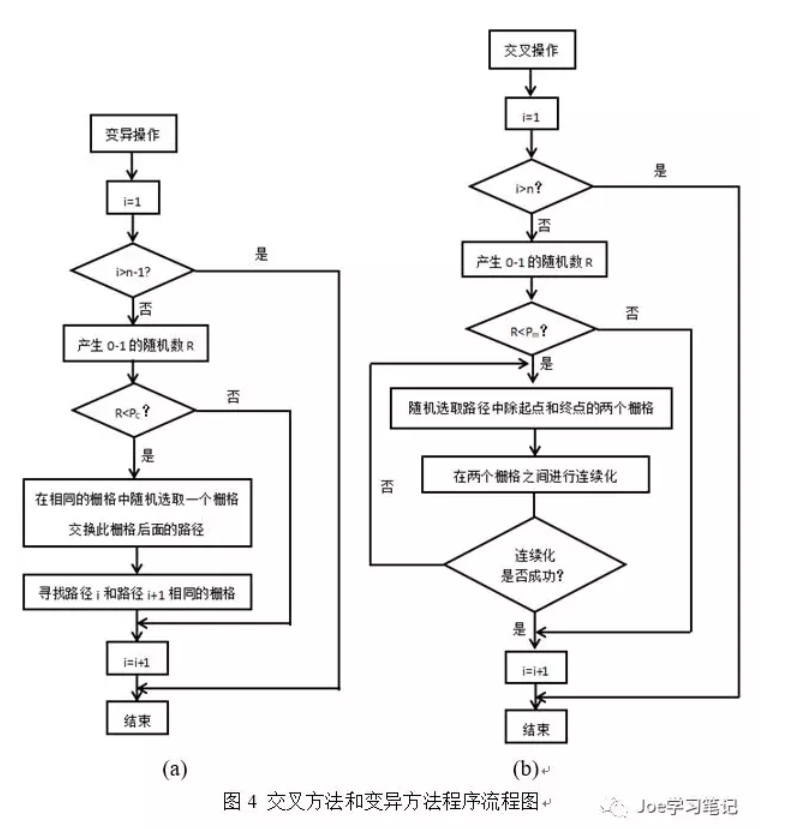
　　首先需要确定一个交叉概率pc，产生0-1之间的一个随机数，并和交叉概率pc比较，若小于pc则进行交叉操作。交叉方式采用的是单点交叉的方式，具体的交叉操作是找出两条路径中所有相同的点，然后随机选择其中的一个点，将之后的路径进行交叉操作。具体的流程图如图4（a）所示，其中n为路径数（即种群数量）。
7.变异方式
　　首先需要确定一个变异概率pm，产生0-1之间的一个随机数，并和变异概率pm比较，若小于pm则进行变异操作。变异方法是随机选取路径中除起点和终点以外的两个栅格，去除这两个栅格之间的路径，然后以这两个栅格为相邻点，使用初始化路径中的第二步将这两个点进行连续操作。此时有可能无法产生连续的路径，则需要重新选择两个栅格执行以上操作，直到完成变异操作。具体的流程图如图3（b）所示，其中n为路径数（即种群数量）。（还是一样把开始和结束框画错了。）

8.仿真结果
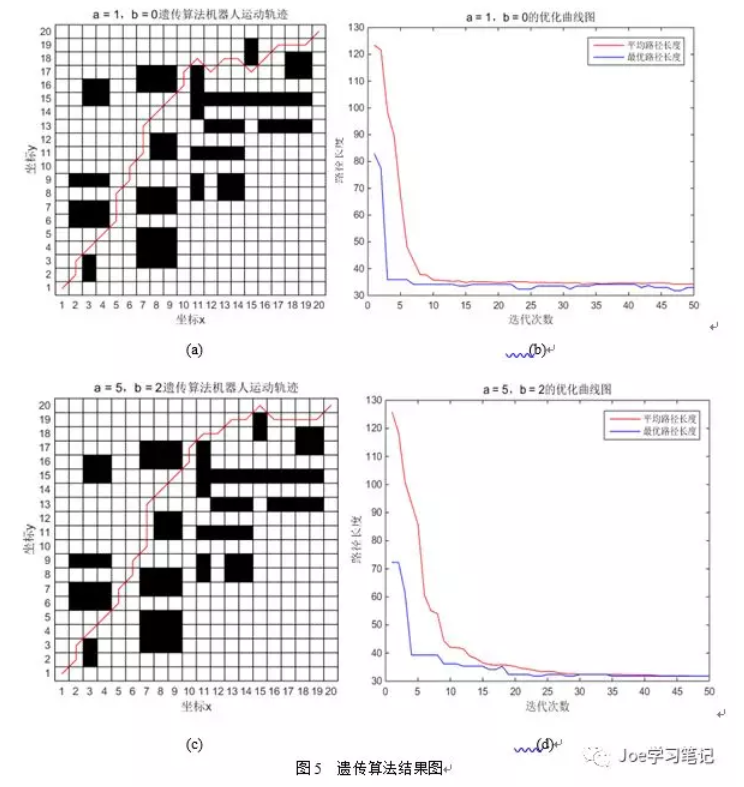
　　在20*20的栅格地图上进行实验，起点为0栅格，终点为399栅格，其中pc=0.8，pm=0.2，a=1，b=0。当b=0即表示不考虑路径的平滑度，只考虑了路径长度作为适应度函数，栅格地图上的路径如图5（a）所示，最短路径如图5（b）所示。从图5（a）中可以看到算法成功的找到了一条无障碍路径，但路径中有多处直角的转折，不利于机器人行驶，有时甚至出现锐角的情况，这种情况一般的机器人是无法行驶的。从图5（b）中得出，经过10次左右迭代算法已经收敛，最优路径的长度为31.799（相邻栅格间隔为1个单位长度）。当a=5，b=2时，即考虑路径平滑度时的算法结果如图5（c）、（d）所示，由于路径顺滑函数中对出现直角的情况加了较大的惩罚，出现锐角的情况加一个无穷大的惩罚，因此顺滑了路径且避免了锐角的出现。此时最优路径的长度也为31.799。

9.总结
　　本文的重点是如何实现基于遗传算法的路径规划算法，首先介绍栅格地图的构建和十进制种群的编码方法。然后给出了整个过程的流程图，在此基础上详细介绍了种群初始化、适应度函数、选择方法、变异方法和交叉方法，并对其中较复杂的种群初始化、变异方法和交叉方法给出了程序流程图。主要的缺点是生成的路径不够平滑，可能是间断路径连续化产生的路径不够平滑，可以在此方面改进，也可以改进适应度函数中的路径平滑的部分，设计更加合理的平滑函数。
　　由于自己水平有限，其中的错误在所难免，大家发现错误可以在下面留言，不懂的地方也可以互相讨论。本文部分内容参考了文献：张小兵. 基于遗传算法的移动机器人路径规划[D]. 西安建筑科技大学, 2014.

最后

以上就是儒雅芒果为你收集整理的基于遗传算法的移动机器人路径规划的全部内容，希望文章能够帮你解决基于遗传算法的移动机器人路径规划所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。