【Eigen】（一）初探

参考：Eigen英文手册

Eigen的API手册写的真心详细，推荐阅读. Eigen中涉及的分解方法主要包括，Cholesky分解、QR分解、SVD分解、特征值分解（eigendecomposition）等.

1、线性求解问题中几种分解方法的比较

针对求解 $Ax=b$ 这种线性问题，Eigen提供了下面几种分解方法，每一种方法都提供了一个solve()函数以便求解得到 $x$，Eigen对每一种分解方法的速度和精度做了如下对比：

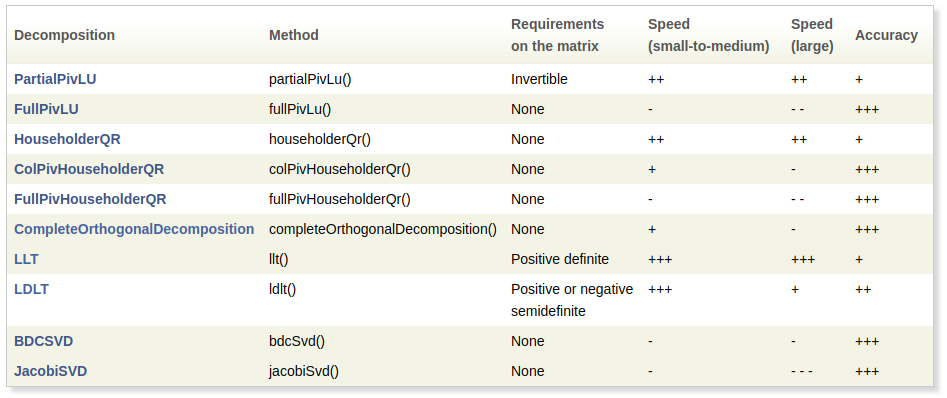
更完整的对比结果在这：https://eigen.tuxfamily.org/dox/group__TopicLinearAlgebraDecompositions.html

实际的速度对比数据在这（注意，测试时使用的矩阵是float类型，如果是double类型的，需要乘2），Cholesky分解需要使用正定的Hermite矩阵，所以在对计算超定矩阵耗时中加入了计算 $A^{T}A$ 的耗时.

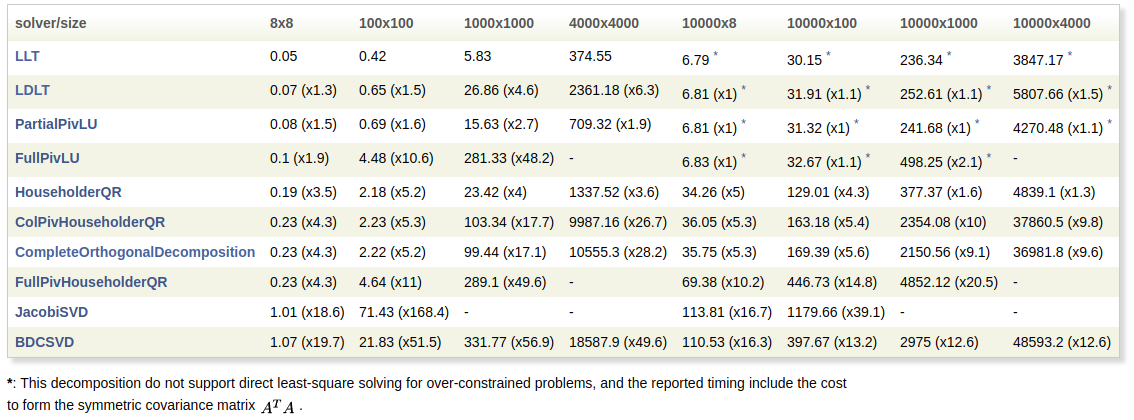
结论：
LLT是最快的求解器，但是精度也是最差的，并且只能对正定矩阵进行分解，而LDLT则可以应对正半定和负半定问题，精度较LLT更高，所以尽量使用LDLT，但是LDLT在求解大矩阵问题时，耗时较QR增加更多，所以究竟选择那种分解方式求解问题，需要根据速度和精度综合考量！

2、使用Eigen的分解方法之前需要注意的地方

2.1 检查解是否存在，带回原方程计算下误差

relative_error = (A*x - b).norm() / b.norm(); // norm() is L2 norm

2.2 计算特征值和特征向量

根据你的矩阵特性选择合适方法：https://eigen.tuxfamily.org/dox/group__TopicLinearAlgebraDecompositions.html
使用info()判断是否收敛（一般都会收敛的）

SelfAdjointEigenSolver<Matrix2f> eigensolver(A);
if (eigensolver.info() != Success) abort();

2.3 计算逆矩阵和行列

如果你的矩阵是小矩阵（$4\times 4$），逆矩阵和行列式随便算，如果是大矩阵就要注意了！
确定你是否真的需要逆矩阵，因为很多时候求逆矩阵都是为了求解 $Ax=b$ 问题，所以最好使用上面介绍的分解方法代替.
如果你计算行列式是为了确定该矩阵是否可逆，那么将很不划算（参照前面两篇博客的内容）

PartialPivLU和FullPivLU中提供了inverse() 和 determinant()的方法，以代替对矩阵直接调用上述方法.

2.4 最小二乘问题求解

最精确的方式是SVD分解，Eigen提供了两个类以实现SVD分解：BDCSVD（大矩阵）和JacobiSVD（小矩阵），推荐使用BDCSVD，因为当发现要分解的矩阵是小矩阵时，将自动切换到JacobiSVD.

2.5 将分解对象构造和分解计算分开

如下，如果将对象构造和分解计算分开的话，这样你就可以重复使用这个对象进行其它矩阵的分解，另外可以选择在构造时使用固定大小，这样可避免内存的动态分配（费时）.

LLT<Matrix3f> dec(A); //同时进行

LLT<Matrix3f> dec2; //分开进行
dec2.compute(A);

HouseholderQR<MatrixXf> qr(50,50);
MatrixXf A = MatrixXf::Random(50,50);
qr.compute(A); // no dynamic memory allocation

2.6 Rank-revealing分解

分解的过程是否能够计算得到矩阵的秩，这种类型的分解能够很好的解决非满秩矩阵（奇异矩阵）问题
提供的函数包括rank()和isInvertible()，也提供了the kernel (null-space) and image (column-space) of the matrix

使用setThreshold()设置rank判定阈值，因为系统使用的阈值是depends on the decomposition but is typically the diagonal size times machine epsilon

Matrix2d A;
A << 2, 1,
	2, 0.9999999999;
FullPivLU<Matrix2d> lu(A);
cout << "By default, the rank of A is found to be " << lu.rank() << endl;
lu.setThreshold(1e-5);
cout << "With threshold 1e-5, the rank of A is found to be " << lu.rank() << endl;

如果不设置阈值，得到的rank将会是2，如果设置为1e-5，将是1

2.7 矩阵的存储顺序选择

1）根据你所使用的算法选择，如果你的算法需要row by row，那么你的矩阵使用RowMajor将会更快！（因为二维矩阵都是展开成一维数据存储在内存里面的）
2）如果你所使用的其它库中也使用Eigen，而这些其它库规定了Eigen矩阵的存储顺序，那么你最好使用这些库中定义的矩阵的存储顺序，比如，g2o中g2o/core/eigen_types.h头文件就定义了它内部使用的矩阵的存储顺序.
3）Eigen默认使用的ColMajor，也就是说，很多Eigen中的很多算法使用的矩阵都是列优先的顺序，所以虽然Eigen同时支持ColMajor和RowMajor，但是ColMajor在Eigen中的效率是最好的，建议使用列优先！（都这样了，我还有得选吗~）

3、LLT和LDLT分解

LLT分解形式：
$$A=L{L}^{\ast }$$
Eigen中的LLT类定义如下

template<typename _MatrixType, int _UpLo> class LLT
{}

_UpLo：表示对矩阵进行LLT分解使用的是其下三角部分（Lower，默认值）还是上三角部分（Upper）

为了使LLT效率最大化，推荐使用column-major storage format with the Lower triangular part或者row-major storage format with the Upper triangular part

LDLT分解形式：
$$A=P^{T}LD{L}^{\ast }P$$

因为LDLT分解中不会用到平方根操作，所以结果更稳定更快，所以如果没有特殊的需要（需要），尽量使用LDLT替代LLT.
并且因为Cholesky不是rank-revealing的，所以不要使用Cholesky分解确定是否有解.

LLT分解时默认只使用的 $A$ 中的下三角部分，并不会检查 $A$ 矩阵的对称性，所以如果你输入的 $A$ 矩阵不是正定的Hermite矩阵 ，你也会得到分解结果，只不过这个结果错误的而已，所以务必确定你要分解的矩阵是对称的.

未完待续…

最后

以上就是坚强茉莉为你收集整理的【Eigen】（一）初探的全部内容，希望文章能够帮你解决【Eigen】（一）初探所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。