矩阵篇（五）-- 特征值分解(EVD)和奇异值分解(SVD)

1 特征值分解（EVD）

        设$A_{n\times n}$有$n$个线性无关的特征向量${\mathbf{x}}_1,\dots ,{\mathbf{x}}_n$，对应特征值分别为${\lambda }_1,\dots ,{\lambda }_n$

$$A\left[\begin{array}{lll}{\mathbf{x}}_1& \cdots & {\mathbf{x}}_n\end{array}\right]=\left[\begin{array}{lll}{\lambda }_1{\mathbf{x}}_1& \cdots & {\lambda }_n{\mathbf{x}}_n\end{array}\right]$$

        所以：
$$A=\left[\begin{array}{lll}{\mathbf{x}}_1& \cdots & {\mathbf{x}}_n\end{array}\right]\left[\begin{array}{lll}{\lambda }_1& & \\ & \ddots & \\ & & {\lambda }_n\end{array}\right]{\left[\begin{array}{lll}{\mathbf{x}}_1& \cdots & {\mathbf{x}}_n\end{array}\right]}^{-1}$$
        因此有EVD分解
$$AX=X\Lambda A=X\Lambda X^{-1}$$
        其中$X$为${\mathbf{x}}_1,\dots ,{\mathbf{x}}_n(列向量)$构成的矩阵，$\Lambda =\mathrm{diag}\left({\lambda }_1,\dots ,{\lambda }_n\right)$。即使固定$\Lambda$，$X$也不唯一。

        更为特殊的是，当矩阵$A$是一个对称矩阵时，则存在一个对称对角化分解，即
$$A=X\Lambda X^T$$
        其中，$X$的每一列都是相互正交的特征向量，且是单位向量，$\Lambda$对角线上的元素是从大到小排列的特征值。

        注意到要进行特征分解，矩阵$A$必须为方阵。那么如果$A$不是方阵，即行和列不相同时，我们还可以对矩阵进行分解吗？答案是可以，此时我们的SVD登场了。

2 奇异值分解（SVD）

2.1 引言

        特征值分解是一个提取矩阵特征很不错的方法，但是它只是对方阵而言的，在现实的世界中，我们看到的大部分矩阵都不是方阵，比如说有$m$个学生，每个学生有$n$科成绩，这样形成的一个$m\times n$的矩阵就不可能是方阵，我们怎样才能描述这样普通的矩阵呢的重要特征呢？奇异值分解可以用来干这个事情，奇异值分解是一个能适用于任意的矩阵的一种分解的方法：
$$A=U\Sigma V^T$$

        假设$A$是一个$m\times n$的矩阵，那么得到的$U$是一个$m\times m$的方阵（里面的向量是正交的，$U$里面的向量称为左奇异向量），$\Sigma$是一个$m\times n$的矩阵（除了对角线的元素都是0，对角线上的元素称为奇异值），$V^T$(V的转置)是一个$n\times m$的矩阵，里面的向量也是正交的，$V$里面的向量称为右奇异向量），从图片来反映几个相乘的矩阵的大小可得下面的图片

        那么奇异值和特征值是怎么对应起来的呢？首先，我们将将A的转置和A做矩阵乘法，将会得到一个方阵，我们用这个方阵求特征值可以得到：
$$(A^{T}A)v_i={\lambda }_i{v}_i$$

        这样我们就可以得到矩阵$A^{T}A$的$n$个特征值和对应的$n$个特征向量$v$了。将$A^{T}A$的所有特征向量张成一个$n\times n$的矩阵$V$，就是我们SVD公式里面的$V$矩阵了。

        如果我们将$A$和$A$的转置做矩阵乘法，那么会得到$m\times m$的一个方阵$A{A}^T$。既然$A{A}^T$是方阵，那么我们就可以进行特征分解，得到的特征值和特征向量满足下式：
$$(A{A}^T)u_i={\lambda }_i{u}_i$$

        这样我们就可以得到矩阵$A{A}^T$的$m$个特征值和对应的$m$个特征向量$u$了。将$A{A}^T$的所有特征向量张成一个$m\times m$的矩阵$U$，就是我们SVD公式里面的$U$矩阵了。

        $U$和$V$我们都求出来了，现在就剩下奇异值矩阵$\Sigma$没有求出了。由于$\Sigma$除了对角线上是奇异值其他位置都是0，那我们只需要求出每个奇异值$\sigma$就可以了。

        我们注意到:
$$A=U\Sigma V^T\Rightarrow AV=U\Sigma V^{T}V\Rightarrow AV=U\Sigma \Rightarrow A{v}_i={\sigma }_i{u}_i\Rightarrow {\sigma }_i=A{v}_i/u_i$$

        进一步我们还可以看出我们的特征值矩阵等于奇异值矩阵的平方，也就是说特征值和奇异值满足如下关系：
$${\sigma }_i=\sqrt{{\lambda }_i}$$

        这里的$\sigma$就是上面说的奇异值，u就是上面说的左奇异向量。奇异值$\sigma$跟特征值类似，在矩阵$\Sigma$中也是从大到小排列，而且$\sigma$的减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上了。也就是说，我们也可以用前$r$大的奇异值来近似描述矩阵，这里定义一下部分奇异值分解：
$$A_{m\times n}\approx U_{m\times r}{\Sigma }_{r\times r}{V}_{r\times n}^T$$

        $r$是一个远小于$m、n$的数，这样矩阵的乘法看起来像是下面的样子：

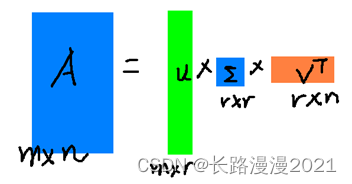
        右边的三个矩阵相乘的结果将会是一个接近于$A$的矩阵，在这儿，$r$越接近于$n$，则相乘的结果越接近于$A$。而这三个矩阵的面积之和（在存储观点来说，矩阵面积越小，存储量就越小）要远远小于原始的矩阵$A$，我们如果想要压缩空间来表示原矩阵$A$，我们存下这里的三个矩阵：$U、\Sigma 、V$就好了。

2.2 定义

        将一个非零的$m\times n$实矩阵$A,A\in R^{m\times n}$，表示为如下三个实矩阵的乘积形式的运算，即进行矩阵的因子分解：

$$A=U\Sigma V^T$$

        其中，$U$是$m$阶正交矩阵，$V$是$n$阶正交矩阵，$\Sigma$是由降序排列的非负对角元素组成的$m\times n$矩形对角矩阵，用符号描述如下：

$$\begin{gathered} U{U}^T=I,V{V}^T=I \\ \Sigma =diag({\sigma }_1,{\sigma }_2,...,{\sigma }_p),{\sigma }_1\ge {\sigma }_2\ge \cdots \ge {\sigma }_p\ge 0,p=min(m,n) \end{gathered}$$

2.3 构造性的证明

1. 求$\Sigma ,V$
        由于$A$是$m\times n$阶的矩阵，所以$A^{T}A$是一个$n\times n$实对称矩阵，故可以对其做正交分解使得：

$$V^T(A^{T}A)V=\Lambda$$

        其中，$V$为n阶正交实矩阵，$\Lambda$为$n$阶对角阵，其对角线元素由$A^{T}A$的特征值构成，且这些特征值非负，下面简单说明，假设$\lambda$是$A^{T}A$的一个特征值，$x$是对应的特征向量，那么

$$||Ax|{|}^2=x^T{A}^{T}Ax=\lambda x^{T}x=\lambda ||x|{|}^2$$

        所以：

$$\lambda =\frac{||Ax|{|}^2}{||x|{|}^2}>0$$

        我们可以通过调整正交矩阵$V$的排列损失使得对应的特征值形成降序排列：

$${\lambda }_1\ge {\lambda }_2\ge \cdots \ge {\lambda }_p\ge 0$$

        接着计算奇异值：

$${\sigma }_j=\sqrt{{\lambda }_j},j=1,2,...,p$$

        假设$A$的秩为$r$，则$A^{T}A$的秩也为r，所以有：

$${\lambda }_1\ge {\lambda }_2\ge \cdots \ge {\lambda }_r>0,{\lambda }_{r+1}={\lambda }_{r+2}=\cdots ={\lambda }_p=0$$

        相应的，我们令：

$$V_1=[v_1,...,v_r],V_2=[v_{r+1},...,v_p]$$

        则：

$$V=[V_1{V}_2]$$

        同样地，我们令：

$${\Sigma }_1=diag({\sigma }_1,...,{\sigma }_r)$$

        对其余部分填充0，使得：

$$\Sigma =\left[\begin{array}{cc}{\Sigma }_1& 0\\ 0& 0\end{array}\right]$$

2. 求$U$

        接下来构造$m$阶正交实对称矩阵$U$，我们令：

$$u_j=\frac{1}{{\sigma }_j}A{v}_j,j=1,2,...,r$$

        令：

$$U_1=[u_1,...,u_r]$$

        那么，如下关系就可以成立了：

$$A{V}_1=U_1{\Sigma }_1$$

        接下来，再为$U_1$扩充$m-r$个标准正交向量，令$[u_{r+1},...,u_m]$为$N(A^T)$的一组正交基，并令：

$$\begin{gathered} U_2=[u_{r+1},...,u_m] \\ U=[U_1{U}_2] \end{gathered}$$

        所以：

$$U\Sigma V^T=\left[\begin{array}{cc}{U}_1& U_2\end{array}\right]\left[\begin{array}{cc}{\Sigma }_1& 0\\ 0& 0\end{array}\right]\left[\begin{array}{c}{V}_1^T\\ V_2^T\end{array}\right]=U_1{\Sigma }_1{V}_1^T=A{V}_1{V}_1^T=A$$

2.4 奇异值分解（SVD）的求法

        第一步：求出${A\text{A}A}_{m\times n}^T{A\text{A}A}_{m\times n}$的 $n$个特征值${\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_r,{\lambda }_{r+1}=0,\cdots ,{\lambda }_n=0$（并按照从大到小排列）和对应的标准正交的特征向量${v\text{v}v}_1,{v\text{v}v}_2,\cdots ,{v\text{v}v}_r,{v\text{v}v}_{r+1},\cdots ,{v\text{v}v}_n$。

        第二步：取标准正交的特征向量构成正交矩阵
$${V\text{V}V}_{n\times n}=({v\text{v}v}_1,{v\text{v}v}_2,\cdots ,{v\text{v}v}_r,{v\text{v}v}_{r+1},\cdots ,{v\text{v}v}_n{)}_{n\times n}$$

        取正奇异值，即前$r$个奇异值，即非零特征值开根号$\sqrt{{\lambda }_1},\sqrt{{\lambda }_2},\cdots ,\sqrt{{\lambda }_r}$，构成对角矩阵
$${D\text{D}D}_{r\times r}={\left(\begin{array}{cccc}\sqrt{{\lambda }_1}& & & \\ & \sqrt{{\lambda }_2}& & \\ & & \ddots & \\ & & & \sqrt{{\lambda }_r}\end{array}\right)}_{r\times r}$$

        添加额外的0组成$m\times n$的矩阵
$${\Sigma \text{Σ}\Sigma }_{m\times n}={\left(\begin{array}{cc}{D\text{D}D}_{r\times r}& 0\text{0}0\\ 0\text{0}0& 0\text{0}0\end{array}\right)}_{m\times n}={\left(\begin{array}{ccccc}\sqrt{{\lambda }_1}& & & & \\ & \sqrt{{\lambda }_2}& & & 0\text{0}0\\ & & \ddots & & \\ & & & \sqrt{{\lambda }_r}& \\ & 0\text{0}0& & & 0\text{0}0\end{array}\right)}_{m\times n}$$

        第三步：构成前$r$个标准正交向量${u\text{u}u}_1,{u\text{u}u}_2,\cdots ,{u\text{u}u}_r$，其中${u\text{u}u}_i=\frac{1}{\sqrt{{\lambda }_i}}A\text{A}A{v\text{v}v}_i,i=1,2,\cdots ,r$

        第四步：将${u\text{u}u}_1,{u\text{u}u}_2,\cdots ,{u\text{u}u}_r$扩充为$m$维向量空间${\mathbb{R}}^m$的标准正交基${u\text{u}u}_1,{u\text{u}u}_2,\cdots ,{u\text{u}u}_r,{b\text{b}b}_1,\cdots ,{b\text{b}b}_{m-r}$，组成正交矩阵
$${U\text{U}U}_{m\times m}=({u\text{u}u}_1,{u\text{u}u}_2,\cdots ,{u\text{u}u}_r,{b\text{b}b}_1,\cdots ,{b\text{b}b}_{m-r}{)}_{m\times m}$$

        第五步：写出即可：
$${A\text{A}A}_{m\times n}={U\text{U}U}_{m\times m}{\Sigma \text{Σ}\Sigma }_{m\times n}{V\text{V}V}_{n\times n}^T={U\text{U}U}_{m\times m}{\left(\begin{array}{ccccc}\sqrt{{\lambda }_1}& & & & \\ & \sqrt{{\lambda }_2}& & & 0\text{0}0\\ & & \ddots & & \\ & & & \sqrt{{\lambda }_r}& \\ & 0\text{0}0& & & 0\text{0}0\end{array}\right)}_{m\times n}{V\text{V}V}_{n\times n}^T$$

2.5 紧奇异值分解

        上面第二节的分解方式称为完全奇异分解，大家可以发现，如果$r<p$，我们完全没有必要对$U_1$以及$V_1$进行扩充，因为通过$U_1,{\Sigma }_1,V_1$就可以无损还原$A$，即：

$$A=U_1{\Sigma }_1{V}_1^T$$

        这便是紧奇异分解。

2.6 截断奇异值分解

        另外，我们也可以只取最大的$k$个奇异值（$k<r$）对应的部分去近似$A$，这便是截断奇异值分解，即：

$$A\approx U_k{\Sigma }_k{V}_k^T$$

        这里，$U_k$是一个$m\times k$的矩阵，由$U$的前$k$列得到，$V_k$是$n\times k$矩阵，由$V$的前$k$列得到，${\Sigma }_k$是$k$阶对角矩阵，由$\Sigma$的前$k$行$k$列得到。

        矩阵$A=[a_{ij}{]}_{m\times n}$的弗罗贝尼乌斯范数定义为
$$\Vert A{\Vert }_F=(\sum _{i=1}^m\sum _{j=1}^n(a_{ij}{)}^2{)}^{\frac{1}{2}}$$

        在秩不超过$k$的$m\times n$矩阵的集合中，存在矩阵$A$的弗罗贝尼乌斯范数意义下的最优近似矩阵$X$。秩为$k$的截断奇异值分解得到的矩阵$A_k$能够达到这个最优值。奇异值分解是弗罗贝尼乌斯范数意义下，也就是平方损失意义下的矩阵最优近似。详细了解，请阅读：奇异值分解的低秩逼近

2.7 案例分析

        SVD的Python实现：

# 实现奇异值分解， 输入一个numpy矩阵，输出 U, sigma, V
# https://zhuanlan.zhihu.com/p/54693391

import numpy as np


#基于矩阵分解的结果，复原矩阵
def rebuildMatrix(U, sigma, V):
    a = np.dot(U, sigma)
    a = np.dot(a, np.transpose(V))
    return a


#基于特征值的大小，对特征值以及特征向量进行排序。倒序排列
def sortByEigenValue(Eigenvalues, EigenVectors):
    index = np.argsort(-1 * Eigenvalues)
    Eigenvalues = Eigenvalues[index]
    EigenVectors = EigenVectors[:, index]
    return Eigenvalues, EigenVectors


#对一个矩阵进行奇异值分解
def SVD(matrixA, NumOfLeft=None):
    #NumOfLeft是要保留的奇异值的个数，也就是中间那个方阵的宽度
    #首先求transpose(A)*A
    matrixAT_matrixA = np.dot(np.transpose(matrixA), matrixA)
    #然后求右奇异向量
    lambda_V, X_V = np.linalg.eig(matrixAT_matrixA)
    lambda_V, X_V = sortByEigenValue(lambda_V, X_V)
    #求奇异值
    sigmas = lambda_V
    sigmas = list(map(lambda x: np.sqrt(x)
                      if x > 0 else 0, sigmas))  #python里很小的数有时候是负数
    sigmas = np.array(sigmas)
    sigmasMatrix = np.diag(sigmas)
    if NumOfLeft == None:
        rankOfSigmasMatrix = len(list(filter(lambda x: x > 0,
                                             sigmas)))  #大于0的特征值的个数
    else:
        rankOfSigmasMatrix = NumOfLeft
    sigmasMatrix = sigmasMatrix[0:rankOfSigmasMatrix, :]  #特征值为0的奇异值就不要了

    #计算右奇异向量
    X_U = np.zeros(
        (matrixA.shape[0], rankOfSigmasMatrix))  #初始化一个右奇异向量矩阵，这里直接进行裁剪
    for i in range(rankOfSigmasMatrix):
        X_U[:, i] = np.transpose(np.dot(matrixA, X_V[:, i]) / sigmas[i])

    #对右奇异向量和奇异值矩阵进行裁剪
    X_V = X_V[:, 0:NumOfLeft]
    sigmasMatrix = sigmasMatrix[0:rankOfSigmasMatrix, 0:rankOfSigmasMatrix]
    #print(rebuildMatrix(X_U, sigmasMatrix, X_V))

    return X_U, sigmasMatrix, X_V

        下面是SVD进图像进行压缩的实践：

import numpy as np
import matplotlib.pyplot as plt

plt.figure(figsize=(18, 4))
im = plt.imread("./demo.jpg")
ks = [800, 500, 200, 100, 50, 10, 5]        # 分别截取不同的 k
for idx, k in enumerate(ks):
    svd_image = []
    for ch in range(3):                     # 注意，有RGB三个维度，每个维度对应一个矩阵做SVD分解
        im_ch = im[:, :, ch]
        U, D, VT = np.linalg.svd(im_ch)
        imx = np.matmul(np.matmul(U[:, :k], np.diag(D[:k])), VT[:k, :])
        # 将像素值约束到合理范围
        imx = np.where(imx<0, 0, imx)
        imx = np.where(imx>255, 255, imx)
        svd_image.append(imx.astype('uint8'))
    img = np.stack((svd_image[0], svd_image[1], svd_image[2]), 2)
    plt.subplot(1, len(ks), idx+1)
    plt.imshow(img)
    plt.axis('off')
    plt.title("k="+str(k))

小结

1. 任意一个$m\times n$ 矩阵，都可以表示为三个矩阵的乘积（因子分解）形式，分别是$m$阶正交矩阵，由降序排列的非负的对角线元素组成的$m$ x $n$ 矩形对角矩阵，和$n$阶正交矩阵，称为该矩阵的奇异值分解。矩阵的奇异值分解一定存在，但不唯一。
2. 奇异值分解可以看作是矩阵数据压缩的一种方法，即用因子分解的方式近似地表示原始矩阵，这种近似是在平方损失意义下的最优近似。
3. 奇异值分解有明确的几何解释。奇异值分解对应三个连续的线性变换：一个旋转变换，一个缩放变换和另一个旋转变换第一个和第三个旋转变换分别基于空间的标准正交基进行。
4. 奇异值分解包括紧奇异值分解和截断奇异值分解。紧奇异值分解是与原始矩阵等秩的奇异值分解，截断奇异值分解是比原始矩阵低秩的奇异值分解。

参考

• 机器学习中的数学(5)-强大的矩阵奇异值分解(SVD)及其应用：https://www.cnblogs.com/LeftNotEasy/archive/2011/01/19/svd-and-applications.html
• 奇异值分解（SVD）的定义、证明、求法（矩阵分解——3. 奇异值分解（SVD））：https://zhuanlan.zhihu.com/p/399547902
• 奇异值分解的揭秘（一）：矩阵的奇异值分解过程：https://zhuanlan.zhihu.com/p/26306568
• 奇异值分解(SVD)原理与在降维中的应用：https://www.cnblogs.com/pinard/p/6251584.html

最后

以上就是陶醉大叔为你收集整理的矩阵篇（五）-- 特征值分解(EVD)和奇异值分解(SVD)的全部内容，希望文章能够帮你解决矩阵篇（五）-- 特征值分解(EVD)和奇异值分解(SVD)所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。