单目影像的空间后方交会Space resection

1.原理

空间交会的目的主要是确定外方位元素。主要类型有两类，一种是已知内方位元素，另外一种是未知内方位元素。但主要原理都大同小异，利用共线方程和最小二乘平差对内外方位元素参数进行解算，这一过程中需要用到一定数量的控制点，以及外方位元素的近似值。
主要的原理就是相机投影中心、相片上点和地物点的共线方程。
$$\begin{gathered} x^{\prime }=x_0^{\prime }+z^{\prime }\frac{r_{11}\cdot (X-X_0)+r_{12}\cdot (Y-Y_0)+r_{31}\cdot (Z-Z_0)}{r_{13}\cdot (X-X_0)+r_{22}\cdot (Y-Y_0)+r_{33}\cdot (Z-Z_0)}+△x^{\prime } \\ {y}^{\prime }=y_0^{\prime }+z^{\prime }\frac{r_{12}\cdot (X-X_0)+r_{22}\cdot (Y-Y_0)+r_{32}\cdot (Z-Z_0)}{r_{13}\cdot (X-X_0)+r_{22}\cdot (Y-Y_0)+r_{33}\cdot (Z-Z_0)}+△y^{\prime } \end{gathered}$$
$(X,Y,Z)$为地物坐标系下的坐标，$(x^{\prime },y^{\prime })$对应图片坐标系下的像素坐标，$z^{\prime }$等于相机焦距的相反数，$△x^{\prime },△y^{\prime }$表示影像的畸变程度，$x_0^{\prime },y_0^{\prime }$表示主点的影像坐标（也即投影中心在影像上的坐标）。

2.已知内方位元素的空间交会

由于有6个外方位元素$X_0,Y_0,Z_0,\omega ,\phi ,\kappa$。所以至少需要3个已知的地面控制点。

通过对上方的共线方程进行线性化，可以获得参数待定的最小二乘形式，从而利用间接平差的方法待定系数。
$$\begin{gathered} v{x}_i^{\prime }=(\frac{\partial x^{\prime }}{\partial X_0}{)}^{0}d{X}_0+(\frac{\partial x^{\prime }}{\partial Y_0}{)}^{0}d{Y}_0+(\frac{\partial x^{\prime }}{\partial Z_0}{)}^{0}d{Z}_0+(\frac{\partial x^{\prime }}{\partial \omega }{)}^{0}d\omega +(\frac{\partial x^{\prime }}{\partial \phi }{)}^{0}d\phi +(\frac{\partial x^{\prime }}{\partial \kappa }{)}^{0}d\kappa +(x_i^{\prime }-x_i^{{}^{\prime }0}) \\ v{y}_i^{\prime }=(\frac{\partial y^{\prime }}{\partial X_0}{)}^{0}d{X}_0+(\frac{\partial y^{\prime }}{\partial Y_0}{)}^{0}d{Y}_0+(\frac{\partial y^{\prime }}{\partial Z_0}{)}^{0}d{Z}_0+(\frac{\partial y^{\prime }}{\partial \omega }{)}^{0}d\omega +(\frac{\partial y^{\prime }}{\partial \phi }{)}^{0}d\phi +(\frac{\partial y^{\prime }}{\partial \kappa }{)}^{0}d\kappa +(y_i^{\prime }-y_i^{{}^{\prime }0}) \end{gathered}$$
其中：
$$\begin{gathered} 令N=r_{13}\cdot (X-X_0)+r_{22}\cdot (Y-Y_0)+r_{33}\cdot (Z-Z_0) \\ {K}_x=r_{11}\cdot (X-X_0)+r_{12}\cdot (Y-Y_0)+r_{31}\cdot (Z-Z_0) \\ {K}_y=r_{12}\cdot (X-X_0)+r_{22}\cdot (Y-Y_0)+r_{32}\cdot (Z-Z_0) \end{gathered}$$
则各个参数的系数为：
$$\begin{gathered} \frac{\partial x^{\prime }}{\partial X_0}=\frac{z^{\prime }}{N^2}\cdot (r_{13}{K}_X-r_{11}N) \\ \frac{\partial x^{\prime }}{\partial Y_0}=\frac{z^{\prime }}{N^2}\cdot (r_{23}{K}_X-r_{21}N) \\ \frac{\partial x^{\prime }}{\partial Z_0}=\frac{z^{\prime }}{N^2}\cdot (r_{33}{K}_X-r_{31}N) \\ \frac{\partial x^{\prime }}{\partial \omega }=\frac{z^{\prime }}{N}\cdot (\frac{K_X}{N}[r_{33}(Y-Y_0)-r_{23}(Z-Z_0)]-r_{31}(Y-Y_0)+r_{21}(Z-Z_0)) \\ \frac{\partial x^{\prime }}{\partial \phi }=\frac{z^{\prime }}{N}\cdot (\frac{K_X}{N}[K_Y\cdot sin\kappa -K_X\cdot cos\kappa ]-N\cdot cos\kappa ) \\ \frac{\partial x^{\prime }}{\partial \kappa }=\frac{z^{\prime }}{N}\cdot K_Y \end{gathered}$$

$$\begin{gathered} \frac{\partial y^{\prime }}{\partial X_0}=\frac{z^{\prime }}{N^2}\cdot (r_{13}{K}_Y-r_{12}N) \\ \frac{\partial y^{\prime }}{\partial Y_0}=\frac{z^{\prime }}{N^2}\cdot (r_{23}{K}_Y-r_{22}N) \\ \frac{\partial y^{\prime }}{\partial Z_0}=\frac{z^{\prime }}{N^2}\cdot (r_{33}{K}_Y-r_{32}N) \\ \frac{\partial y^{\prime }}{\partial \omega }=\frac{z^{\prime }}{N}\cdot (\frac{K_Y}{N}[r_{33}(Y-Y_0)-r_{23}(Z-Z_0)]-r_{32}(Y-Y_0)+r_{22}(Z-Z_0)) \\ \frac{\partial y^{\prime }}{\partial \phi }=\frac{z^{\prime }}{N}\cdot (\frac{K_Y}{N}[K_Y\cdot sin\kappa -K_X\cdot cos\kappa ]+N\cdot sin\kappa ) \\ \frac{\partial y^{\prime }}{\partial \kappa }=-\frac{z^{\prime }}{N}\cdot K_X \end{gathered}$$

3.参数近似值的确定

可以通过GPS和INS方式确定参数近似值；可以通过拍照相机的姿态（如果相机相片几乎平行于地物系，则旋转角可以被认为都为0）和相机的放大倍数及参考点坐标（$X_0,Y_0$通过重心确定，$Z-Z_0$通过主句和相机放大倍数确定）；通常的方法，普适的方式就是通过几何条件进行计算参数近似值。

之所以需要参数的近似值，是共线方程模型是非线性化模型，最小二乘在计算过程中如果参数没有近似值，就可能会无法收敛。所以参数近似值是必要。

计算参数近似值的过程是通过获取相机坐标系下地物点的坐标，再与地物系下地物点的坐标进行7参数转换获得的。而地物点的坐标是通过四面体交会的方式通过迭代获取的。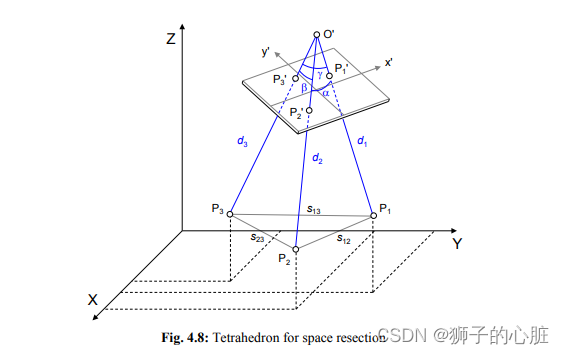

根据已知数据的情况，其中上图$s_{13},s_{23},s_{12}$是已知的，因为地物点坐标已知；又内方位元素已知，所以$P_1^{\prime },P_2^{\prime },P_3^{\prime },0^{\prime }$坐标是已知的，其中$O^{\prime }$坐标为(0,0,0)，$P$对应的z轴坐标为$-c$(即焦距的相反数)。进而可以计算出夹角$\alpha ,\beta ,\gamma$，进而目的是为了确定$d_1,d_2,d_3$。根据四面体下底面三条边和上顶角三个角的确定情况，可以确定几组备选方案，从中获取到的几组数据用来通过筛选就可以得到最终的结果，或者逐一进行平差看哪组可以使结果收敛，就选择哪一组。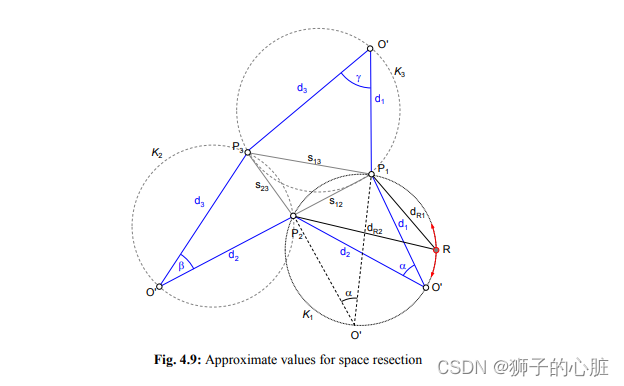

$s_{13},s_{23},s_{12}$是已知的，夹角$\alpha ,\beta ,\gamma$是已知的，所以可以首先假定$d_1$是一个很小的值，通过正弦定理

$d_2=sin\angle \alpha \ast \frac{d_1}{sin\angle O^{\prime }{P}_2^{\prime }{P}_1^{\prime }}$

再不断向后面的三角形推过去，就可以最终推回到$d_1$，判断与初始情况的$d_1$相差多大，如果相差非常小的情况下，则可以认为蓝色的三个三角可以交会到相机投影中心。然后不断扩大$d_1$，不断找下去。

已知了$d_1,d_2,d_3$就可以利用$O^{\prime }{P}_i^{\prime }$与$O^{\prime }{P}_i$之间的距离比值获得到相机 坐标系下地物点的坐标：
$$\begin{gathered} d=\sqrt{x^{{}^{\prime }2}+y^{{}^{\prime }2}+z^{{}^{\prime }2}} \\ {x}_i=\frac{d_i}{d_i^{\prime }}\cdot x_i^{\prime } \\ {y}_i=\frac{d_i}{d_i^{\prime }}\cdot y_i^{\prime } \\ {z}_i=\frac{d_i}{d_i^{\prime }}\cdot z_i^{\prime } \end{gathered}$$
然后就可以利用7参数转换，获取相机坐标系下和地物坐标系下地物点的坐标转换关系，也即共线方程中参数的近似值了。同样需要注意7参数转换与外方位元素之间的区别，弄清楚到底是哪个坐标系向哪个坐标系转换！

在计算近似值的过程中，$O^{\prime }$透视中心和$R$旋转矩阵可能不唯一，就要用第四个点进行检验，通过将地物系下图像点$(X,Y,Z)$利用坐标转换转化到相片上，然后与相片上的点$(x,y)$进行比较，如果相近则是较优的近似值。

检验，通过将地物系下图像点$(X,Y,Z)$利用坐标转换转化到相片上，然后与相片上的点$(x,y)$进行比较，如果相近则是较优的近似值。

4.代码实现

单目影像的空间后方交会代码

最后

以上就是健康小丸子为你收集整理的【后方交会】单目影像的空间后方交会Space resection单目影像的空间后方交会Space resection的全部内容，希望文章能够帮你解决【后方交会】单目影像的空间后方交会Space resection单目影像的空间后方交会Space resection所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。