本文不详细说明空间后方交会的原理,只着重说明空间后方交会的程序,并附带一个样例。
样例来源:《摄影测量学》(第二版)武汉大学出版社,张剑清,潘励,王树根。
空间后方交会的误差方程式:
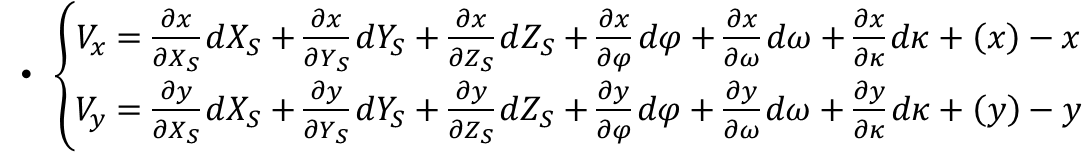
可以简写为: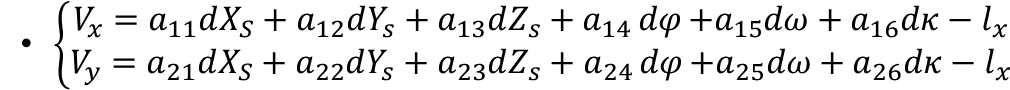
写成矩阵形式:
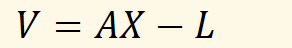
根据误差方程式列出法方程式:
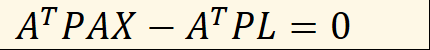
整理可得:
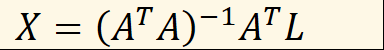
其中:
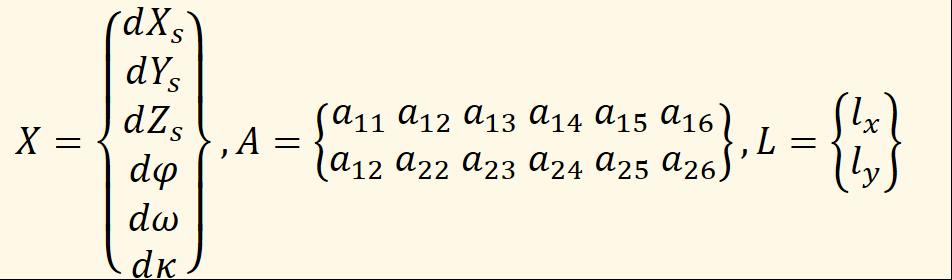
以下是代码实现:
分为四个文件:main.cpp,Matrix.h(矩阵类),SpaceResection.h(空间后方交会的函数声明和宏定义),SpaceResection.cpp(空间后方交会的函数实现)
main.cpp:
#pragma once
#include <iomanip>
#include "SpaceResection.h"
int main()
{
//定义变量
vector<G_point> ground;//地面坐标
vector<P_point> photo;//像点坐标
vector<P_point> approx(pointNum);//像点坐标近似值
double Xs = 0.0, Ys = 0.0, Zs = 0.0, t = 0.0, w = 0.0, k = 0.0;//外方位元素
Matrix<double> R(3, 3);//旋转矩阵R
//法方程式矩阵的解 X = (A的转置 * A)的逆矩阵 * A的转置 * L
Matrix<double> X;//外方位元素的改正数,是需要求解的矩阵
Matrix<double> A(pointNum * 2, 6);//误差方程式中的偏导数
Matrix<double> L(pointNum * 2, 1);//误差方程式中的常数项
//定义变量
//空间后方交会的求解
//(1)获取已知数据
//(2)确定未知数初值
//(3)计算旋转矩阵R
//(4)逐点计算像点坐标近似值(x),(y)和误差方程式中的系数和常数项并组成法方程式
//(5)按照法方程式解的表达式求外方位元素改正值Xs,Ys,Zs,t,w,k
//(6)检查所得改正数是否小于给定限值,若不是,重复步骤(3)~(5),直到满足要求为止
//(1)获取已知数据
getGpoint(ground);//获取地面控制点坐标
getPpoint(photo);//获取像点坐标
//(2)确定未知数初值
init(Xs, Ys, Zs, t, w, k, ground);//确定未知数的初值
//迭代步骤(3)~(5)
do
{
//(3)计算旋转矩阵R
cal_Matrix_R(R, t, w, k);
for (int i = 0; i < pointNum; ++i)
{
//(4)逐点计算像点坐标近似值(x),(y)和误差方程式中的系数和常数项并组成法方程式
approx[i].x = -f * (R[0][0] * (ground[i].x - Xs) + R[1][0] * (ground[i].y - Ys)
+ R[2][0] * (ground[i].z - Zs)) / (R[0][2] * (ground[i].x - Xs) + R[1][2]
* (ground[i].y - Ys) + R[2][2] * (ground[i].z - Zs));
approx[i].y = -f * (R[0][1] * (ground[i].x - Xs) + R[1][1] * (ground[i].y - Ys)
+ R[2][1] * (ground[i].z - Zs)) / (R[0][2] * (ground[i].x - Xs) + R[1][2]
* (ground[i].y - Ys) + R[2][2] * (ground[i].z - Zs));
//计算误差方程式的系数和常数项并组成法方程式
double Z = R[0][2] * (ground[i].x - Xs) + R[1][2] * (ground[i].y - Ys) +
R[2][2] * (ground[i].z - Zs);//便于计算矩阵A
cal_Matrix_A(A, R, photo, Z, i, t, w, k);//计算矩阵A
cal_Matrix_L(L, photo, approx, i);//计算矩阵L
}
//(5)按照法方程式解的表达式求外方位元素改正值Xs,Ys,Zs,t,w,k
X = (A.transpsition() * A).inverse() * A.transpsition() * L;
correction(Xs, Ys, Zs, t, w, k, X);//修正外方位元素的值
} while (!isLessLimit(X));//(6)检查所得改正数是否小于给定限值
cout << "Xs = " << fixed << setprecision(2) << Xs << endl;
cout << "Ys = " << fixed << setprecision(2) << Ys << endl;
cout << "Zs = " << fixed << setprecision(2) << Zs << endl;
cout << "t = " << fixed << setprecision(5) << t << endl;
cout << "w = " << fixed << setprecision(5) << w << endl;
cout << "k = " << fixed << setprecision(5) << k << endl;
cout << "R矩阵:" << endl;
cout << fixed << setprecision(5) << R << endl;
system("pause");
return 0;
}
SpaceResection.h:
#pragma once
#include <iostream>
#include <vector>
#include "Matrix.h"
//内方位元素(mm)
#define x0 0
#define y0 0
#define f (153.24/1000.0)//焦距(mm)
#define m 50000//像片比例尺
#define pointNum 4//地面控制点的数量
#define LIMIT 0.01//限值
//大地坐标(m)
typedef struct G_point
{
double x;
double y;
double z;
}G_point;
//像片坐标(mm)
typedef struct P_point
{
double x;
double y;
}P_point;
//获取地面控制点的坐标
void getGpoint(std::vector<G_point>& G);
//获取像点坐标
void getPpoint(std::vector<P_point>& P);
//确定未知数初值
void init(double& Xs, double& Ys, double& Zs, double& t, double& w, double& k, const std::vector<G_point>& G);
//计算旋转矩阵R
void cal_Matrix_R(Matrix<double>& R, const double t, const double w, const double k);
//计算误差方程式的系数
void cal_Matrix_A(Matrix<double>& A, Matrix<double>& R, vector<P_point>& P, double Z,
int i, double t, double w, double k);
//计算L矩阵
void cal_Matrix_L(Matrix<double>& L, const vector<P_point>& P, const vector<P_point>& Ap, int i);
//修正外方位元素
void correction(double& Xs, double& Ys, double& Zs, double& t, double& w, double& k,
Matrix<double>& X);
//判断未知数改正数是否小于限值
bool isLessLimit(Matrix<double>& ma);
SpaceResection.cpp
#include "SpaceResection.h"
void getGpoint(std::vector<G_point>& G)
{
G.reserve(pointNum);
G.resize(pointNum);
for (std::vector<G_point>::iterator it = G.begin(); it != G.end(); ++it)
{
std::cin >> (*it).x >> (*it).y >> (*it).z;
}
}
void getPpoint(std::vector<P_point>& P)
{
P.reserve(pointNum);
P.resize(pointNum);
for (std::vector<P_point>::iterator it = P.begin(); it != P.end(); ++it)
{
std::cin >> (*it).x >> (*it).y;
(*it).x /= 1000.0;
(*it).y /= 1000.0;
}
}
void init(double & Xs, double & Ys, double & Zs, double & t, double & w, double & k,
const std::vector<G_point> & G)
{
double Z = 0;
for (std::vector<G_point>::const_iterator it = G.cbegin(); it != G.cend(); ++it)
{
Xs += (*it).x;
Ys += (*it).y;
Z += (*it).z;
}
Xs /= pointNum;
Ys /= pointNum;
Zs = m * f + Z / pointNum;
t = 0.0;
w = 0.0;
k = 0.0;
}
void cal_Matrix_R(Matrix<double>& R, const double t, const double w, const double k)
{
R[0][0] = cos(t) * cos(k) - sin(t) * sin(w) * sin(k);
R[0][1] = -cos(t) * sin(k) - sin(t) * sin(w) * cos(k);
R[0][2] = -sin(t) * cos(w);
R[1][0] = cos(w) * sin(k);
R[1][1] = cos(w) * cos(k);
R[1][2] = -sin(w);
R[2][0] = sin(t) * cos(k) + cos(t) * sin(w) * sin(k);
R[2][1] = -sin(t) * sin(k) + cos(t) * sin(w) * cos(k);
R[2][2] = cos(t) * cos(w);
}
void cal_Matrix_A(Matrix<double>& A, Matrix<double>& R, vector<P_point>& P, double Z,
int i, double t, double w, double k)
{
A[i * 2][0] = (R[0][0] * f + R[0][2] * P[i].x) / Z;//a11
A[i * 2][1] = (R[1][0] * f + R[1][2] * P[i].x) / Z;//a12
A[i * 2][2] = (R[2][0] * f + R[2][2] * P[i].x) / Z;//a13
A[i * 2][3] = P[i].y * sin(w) - (P[i].x * (P[i].x * cos(k)
- P[i].y * sin(k)) / f + f * cos(k)) * cos(w);//a14
A[i * 2][4] = -f * sin(k) - P[i].x * (P[i].x * sin(k)
+ P[i].y * cos(k)) / f;//a15
A[i * 2][5] = P[i].y;//a16
A[i * 2 + 1][0] = (R[0][1] * f + R[0][2] * P[i].y) / Z;//a21
A[i * 2 + 1][1] = (R[1][1] * f + R[1][2] * P[i].y) / Z;//a22
A[i * 2 + 1][2] = (R[2][1] * f + R[2][2] * P[i].y) / Z;//a23
A[i * 2 + 1][3] = -P[i].x * sin(w) - (P[i].y * (P[i].x * cos(k)
- P[i].y * sin(k)) / f - f * sin(k)) * cos(w);//a24
A[i * 2 + 1][4] = -f * cos(k) - (P[i].y * (P[i].x * sin(k)
+ P[i].y * cos(k))) / f;//a25
A[i * 2 + 1][5] = -P[i].x;//a26
}
void cal_Matrix_L(Matrix<double>& L, const vector<P_point>& P, const vector<P_point>& Ap, int i)
{
L[i * 2][0] = P[i].x - Ap[i].x;
L[i * 2 + 1][0] = P[i].y - Ap[i].y;
}
void correction(double& Xs, double& Ys, double& Zs, double& t, double& w, double& k, Matrix<double>& X)
{
Xs += X[0][0];
Ys += X[1][0];
Zs += X[2][0];
t += X[3][0];
w += X[4][0];
k += X[5][0];
}
bool isLessLimit(Matrix<double>& ma)
{
if (fabs(ma[3][0]) < LIMIT && fabs(ma[4][0]) < LIMIT && fabs(ma[5][0]) < LIMIT)
return true;
return false;
}
Matrix.h:
#pragma once
using namespace std;
template <typename T>
class Matrix
{
public:
int _line;
int _row;
T _matrix[10][10];
public:
Matrix();//默认2行2列元素全为0的矩阵
Matrix(int line, int row);//line行row列元素全为0的矩阵
Matrix(int line, int row, T data);//line行row列元素全为data的矩阵
//转置矩阵
Matrix<T> transpsition() const;
//第line行row列的余子式
Matrix<T> minor(int line, int row) const;
//求矩阵的值
double value() const;
//伴随矩阵
Matrix<T> adjoint() const;
//逆矩阵
Matrix<T> inverse() const;
//矩阵的运算符重载
Matrix<T> operator+(const Matrix<T>& ma) const;
Matrix<T> operator-(const Matrix<T>& ma) const;
Matrix<T> operator*(const Matrix<T>& ma) const;
Matrix<T> operator*(double a) const;
Matrix<T> operator/(double a) const;
Matrix<T> operator=(const Matrix<T>& ma);
friend Matrix<T> operator*(double a, const Matrix<T>& ma)
{
Matrix<T> temp(ma._line, ma._row);
for (int i = 0; i < ma._line; i++)
{
for (int j = 0; j < ma._row; j++)
{
temp._matrix[i][j] = ma._matrix[i][j] * a;
}
}
return temp;
}
friend Matrix<T> operator/(double a, const Matrix<T>& ma)
{
Matrix<T> temp(ma._line, ma._row);
for (int i = 0; i < ma._line; i++)
{
for (int j = 0; j < ma._row; j++)
{
temp._matrix[i][j] = ma._matrix[i][j] / a;
}
}
return temp;
}
friend istream& operator>>(istream& is, Matrix<T>& ma)
{
for (int i = 0; i < ma._line; ++i)
{
for (int j = 0; j < ma._row; ++j)
{
is >> ma._matrix[i][j];
}
}
return is;
}
friend ostream& operator<<(ostream& os, const Matrix<T>& ma)
{
for (int i = 0; i < ma._line; ++i)
{
for (int j = 0; j < ma._row; ++j)
{
os << ma._matrix[i][j] << " ";
}
os << endl;
}
return os;
}
T* operator[](const int r);
};
template <typename T>
Matrix<T>::Matrix() :_line(2), _row(2)
{
for (int i = 0; i < 10; ++i)
for (int j = 0; j < 10; ++j)
_matrix[i][j] = 0.0;
}
template<typename T>
Matrix<T>::Matrix(int line, int row) : _line(line), _row(row)
{
for (int i = 0; i < 10; ++i)
for (int j = 0; j < 10; ++j)
_matrix[i][j] = 0.0;
}
template<typename T>
Matrix<T>::Matrix(int line, int row, T data) : _line(line), _row(row)
{
for (int i = 0; i < 10; ++i)
for (int j = 0; j < 10; ++j)
_matrix[i][j] = 0.0;
for (int i = 0; i < _line; ++i)
for (int j = 0; j < _row; ++j)
_matrix[i][j] = data;
}
template<typename T>
Matrix<T> Matrix<T>::transpsition() const
{
Matrix<T> temp(_row, _line);
for (int i = 0; i < _line; ++i)
for (int j = 0; j < _row; ++j)
temp._matrix[j][i] = _matrix[i][j];
return temp;
}
template<typename T>
Matrix<T> Matrix<T>::minor(int line, int row) const
{
if (line < 0 || row < 0 || line >= _line || row >= _row)
{
cout << "余子式出错" << endl;
return *this;
}
Matrix<T> temp(_line - 1, _row - 1);
for (int i = 0, tempi = 0; i < _line; i++)
{
if (i == line)
continue;
for (int j = 0, tempj = 0; j < _row; j++)
{
if (j == row)
continue;
else
{
temp._matrix[tempi][tempj] = _matrix[i][j];
tempj++;
}
}
tempi++;
}
return temp;
}
template<typename T>
double Matrix<T>::value() const
{
double res = 0;
if (_line != _row)
{
cout << "求矩阵的值出错:必须是方阵才能求值" << endl;
return -1;
}
if (1 == _line)
{
return _matrix[0][0];
}
if (2 == _line)
{
return _matrix[0][0] * _matrix[1][1] - _matrix[0][1] * _matrix[1][0];
}
else
{
for (int i = 0; i < _line; ++i)
{
if (i % 2 == 0)
{
res += (minor(i, 0).value() * _matrix[i][0]);
}
else
{
res += (minor(i, 0).value() * (_matrix[i][0]) * -1);
}
}
}
return res;
}
template<typename T>
inline Matrix<T> Matrix<T>::adjoint() const
{
if (_line != _row)
{
cout << "求伴随矩阵出错" << endl;
return *this;
}
Matrix<T> temp(_line, _row);
for (int i = 0; i < _line; i++)
{
for (int j = 0; j < _row; j++)
{
if ((i + j) % 2 == 0)
{
temp._matrix[i][j] = minor(j, i).value();
}
else
{
temp._matrix[i][j] = minor(j, i).value() * -1.0;
}
}
}
return temp;
}
template<typename T>
Matrix<T> Matrix<T>::inverse() const
{
if (this->value() == 0.0)
{
cout << "求逆矩阵出错:矩阵的值不能为0" << endl;
return *this;
}
Matrix<T> temp(_line, _row);
temp = adjoint() / value();
return temp;
}
template<typename T>
Matrix<T> Matrix<T>::operator+(const Matrix<T>& ma) const
{
if (_line != ma._line || _row != ma._row)
{
cout << "矩阵相加出错" << endl;
return *this;
}
Matrix<T> temp(_line, _row);
for (int i = 0; i < _line; ++i)
{
for (int j = 0; j < _row; ++j)
{
temp._matrix[i][j] = _matrix[i][j] + ma._matrix[i][j];
}
}
return temp;
}
template<typename T>
Matrix<T> Matrix<T>::operator-(const Matrix<T>& ma) const
{
if (_line != ma._line || _row != ma._row)
{
cout << "矩阵相减出错" << endl;
return *this;
}
Matrix<T> temp(_line, _row);
for (int i = 0; i < _line; ++i)
{
for (int j = 0; j < _row; ++j)
{
temp._matrix[i][j] = _matrix[i][j] - ma._matrix[i][j];
}
}
return temp;
}
template<typename T>
Matrix<T> Matrix<T>::operator*(const Matrix<T>& ma) const
{
if (_row != ma._line)
{
cout << "矩阵相乘出错" << endl;
return *this;
}
Matrix<T> temp(_line, ma._row);
for (int i = 0; i < _line; i++)
{
for (int j = 0; j < ma._row; j++)
{
for (int k = 0; k < _row; k++)
{
temp._matrix[i][j] += _matrix[i][k] * ma._matrix[k][j];
}
}
}
return temp;
}
template<typename T>
Matrix<T> Matrix<T>::operator*(double a) const
{
Matrix<T> temp(_line, _row);
for (int i = 0; i < _line; i++)
{
for (int j = 0; j < _row; j++)
{
temp._matrix[i][j] = _matrix[i][j] * a;
}
}
return temp;
}
template<typename T>
Matrix<T> Matrix<T>::operator/(double a) const
{
Matrix<T> temp(_line, _row);
for (int i = 0; i < _line; i++)
{
for (int j = 0; j < _row; j++)
{
temp._matrix[i][j] = _matrix[i][j] / a;
}
}
return temp;
}
template<typename T>
inline Matrix<T> Matrix<T>::operator=(const Matrix<T>& ma)
{
_line = ma._line;
_row = ma._row;
for (int i = 0; i < _line; ++i)
{
for (int j = 0; j < _row; ++j)
{
_matrix[i][j] = ma._matrix[i][j];
}
}
return *this;
}
template<typename T>
inline T* Matrix<T>::operator[](const int r)
{
return _matrix[r];
}
样例数据(数据来源在本文开头):
36589.41 25273.32 2195.17
37631.08 31324.51 728.69
39100.97 24934.98 2386.50
40426.54 30319.81 757.31
-86.15 -68.99
-53.40 82.21
-14.78 -76.63
10.46 64.43
样例输出:
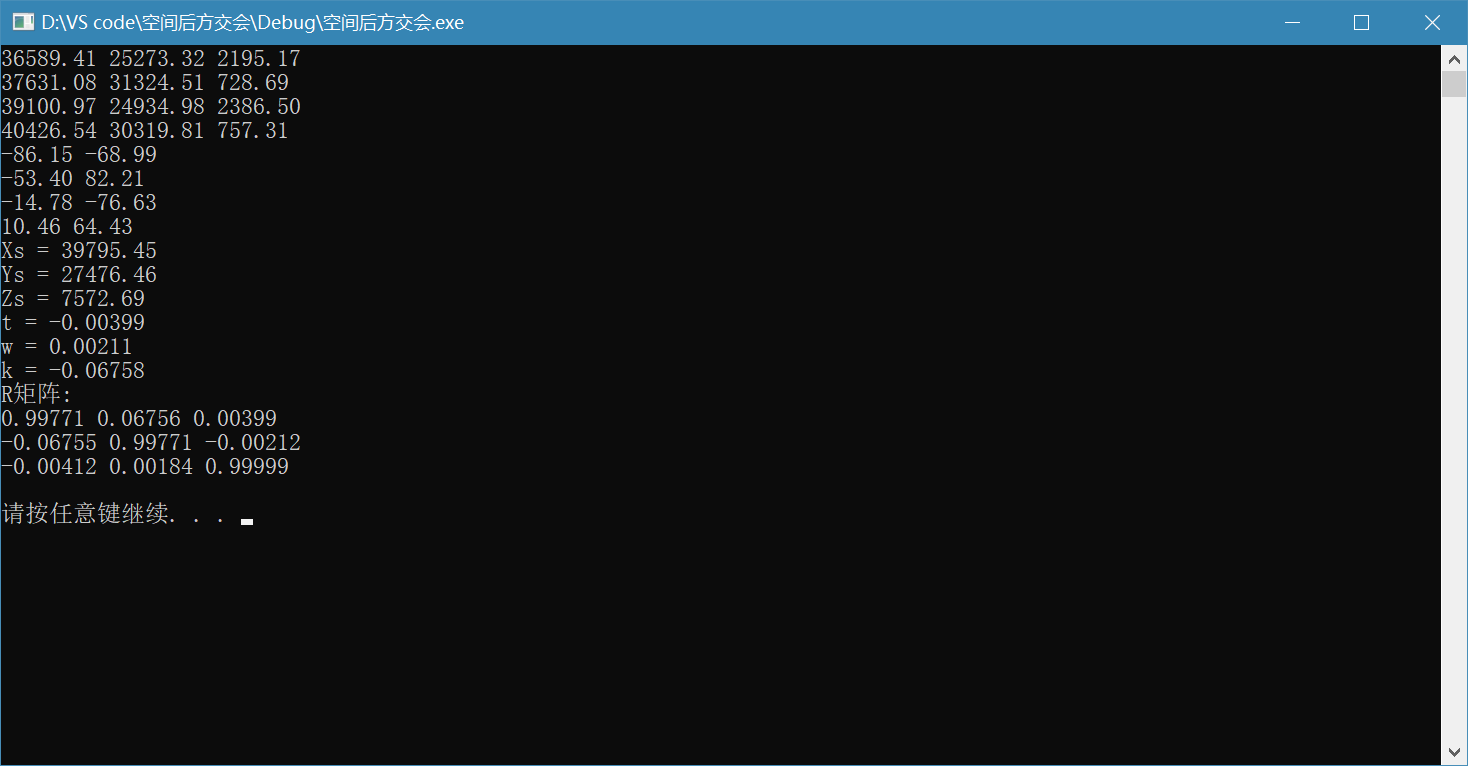
后续还会添加matlab实现。
%像片比例尺
m = 50000;
%内方位元素(mm)
x0 = 0;
y0 = 0;
f = 153.24 / 1000.0;
%------------------读取数据和存储数据-------------------%
%-----GROUND地面坐标(m)
%-----PHOTO像片坐标(mm)
%-----把地面坐标放到ground.txt文件中--------------------------
%-----把像片坐标放到photo.txt文件中-----------------------
%-----然后将这两个文件放到对应的文件夹里
fid = fopen('ground.txt','r');
g = textscan(fid,'%f %f %f');
fclose(fid);
GROUND = [g{1}, g{2}, g{3}];
fid = fopen('photo.txt','r');
p = textscan(fid, '%f %f');
fclose(fid);
PHOTO = [p{1}, p{2}];
PHOTO = PHOTO / 1000.0; %单位转换,mm转为m
%-----pointNum矩阵的行数,即控制点个数 pointNum = size(GROUND,1);
%-----------------给定待求参数初值------------------
%-----六个待求外方位元素Xs,Ys,Zs,t,w,k
Xs = sum(GROUND(:,1)) / pointNum;
Ys = sum(GROUND(:,2)) / pointNum;
Zs = sum(GROUND(:,3)) / pointNum + m * f;
t = 0.0;
w = 0.0;
k = 0.0;
%----------------A矩阵和L矩阵------------------------
%-----A--误差方程式中的系数项(偏导数)
%-----L--误差方程式中的常数项
A = zeros(pointNum * 2, 6);
L = zeros(pointNum * 2, 1);
%-----------------------迭代计算-----------------------
while (1)
%------------------------计算旋转矩阵R-----------------------
a(1) = cos(t) * cos(k) - sin(t) * sin(w) * sin(k);
a(2) = -cos(t) * sin(k) - sin(t) * sin(w) * cos(k);
a(3) = -sin(t) * cos(w);
b(1) = cos(w) * sin(k);
b(2) = cos(w) * cos(k);
b(3) = -sin(w);
c(1) = sin(t) * cos(k) + cos(t) * sin(w) * sin(k);
c(2) = -sin(t) * sin(k) + cos(t) * sin(w) * cos(k);
c(3) = cos(t) * cos(w);
%----------------逐点计算像片坐标近似值-----------------------
%-----逐点计算误差方程式中的常数项和系数项并组成矩阵-----------------
for i = 1:pointNum
%---------------求像片近似坐标(x),(y)-----------------
ap(1) = -f * (a(1) * (GROUND(i,1) - Xs) + b(1) * (GROUND(i, 2) - Ys) + c(1) * (GROUND(i,3) - Zs)) / (a(3) * (GROUND(i, 1) - Xs) + b(3) * (GROUND(i, 2) - Ys) + c(3) * (GROUND(i, 3) - Zs));
ap(2) = -f * (a(2) * (GROUND(i,1) - Xs) + b(2) * (GROUND(i, 2) - Ys) + c(2) * (GROUND(i,3) - Zs)) / (a(3) * (GROUND(i, 1) - Xs) + b(3) * (GROUND(i, 2) - Ys) + c(3) * (GROUND(i, 3) - Zs));
%--------------------------A矩阵---------------------
Zbar = a(3) * (GROUND(i, 1) - Xs) + b(3) * (GROUND(i, 2) - Ys) + c(3) * (GROUND(i, 3) - Zs);
A(i * 2 - 1, 1) = (a(1) * f + a(3) * PHOTO(i, 1)) / Zbar;
A(i * 2 - 1, 2) = (b(1) * f + b(3) * PHOTO(i, 1)) / Zbar;
A(i * 2 - 1, 3) = (c(1) * f + c(3) * PHOTO(i, 1)) / Zbar;
A(i * 2 - 1, 4) = PHOTO(i, 2) * sin(w) - (PHOTO(i, 1) * (PHOTO(i, 1) * cos(k) - PHOTO(i, 2) * sin(k)) / f + f * cos(k)) * cos(w);
A(i * 2 - 1, 5) = -f * sin(k) - PHOTO(i, 1) * (PHOTO(i, 1) * sin(k) + PHOTO(i, 2) * cos(k)) / f;
A(i * 2 - 1, 6) = PHOTO(i, 2);
A(i * 2, 1) = (a(2) * f + a(3) * PHOTO(i, 2)) / Zbar;
A(i * 2, 2) = (b(2) * f + b(3) * PHOTO(i, 2)) / Zbar;
A(i * 2, 3) = (c(2) * f + c(3) * PHOTO(i, 2)) / Zbar;
A(i * 2, 4) = PHOTO(i, 1) * sin(w) - (PHOTO(i, 2) * (PHOTO(i, 1) * cos(k) - PHOTO(i, 2) * sin(k)) / f - f * sin(k)) * cos(w);
A(i * 2, 5) = -f * cos(k) - PHOTO(i, 2) * (PHOTO(i, 1) * sin(k) + PHOTO(i, 2) * cos(k)) / f;
A(i * 2, 6) = -PHOTO(i, 1);
%--------------L矩阵------------------
L(i * 2 - 1, 1) = PHOTO(i, 1) - ap(1);
L(i * 2, 1) = PHOTO(i, 2) - ap(2);
end
%-----------------解外方位元素改正值-----------------------
%-----X是一个列向量,存放一次计算之后外方位元素的改正数
X = (A' * A) A' * L;
%--------------------修正外方位元素------------------
Xs = X(1) + Xs;
Ys = X(2) + Ys;
Zs = X(3) + Zs;
t = X(4) + t;
w = X(5) + w;
k = X(6) + k;
%----------------判断改正值是否小于给定限值----------------
%-----小于给定限值则退出循环
%-----若不满足要求则继续计算,直到满足要求为止
if abs(X(4)) < 0.01 && abs(X(5)) < 0.01 && abs(X(6)) < 0.01
break;
end
end
%-------------------输出所求得的参数--------------
fprintf('Xs = %fnYs = %fnZs = %fn', Xs, Ys, Zs); fprintf('t = %fnw = %fnk = %fn, t, w, k);
fprintf('R:n'); fprintf('%f %f %fn', a(1), a(2), a(3)); fprintf('%f %f %fn', b(1), b(2), b(3)); fprintf('%f %f %fn', c(1), c(2), c(3));
最后
以上就是野性小土豆最近收集整理的关于空间后方交会c++程序和matlab(可直接运行)的全部内容,更多相关空间后方交会c++程序和matlab(可直接运行)内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复