Matlab 关于补零和延拓来提高FFT分辨率

在处理某段信号的过程中，遇到了频率分辨率的问题，原始数据1s，但是我想要0.1Hz的频率分辨率，经过一番百度，知道了重复数据和补零2种方法，但是这两种方法会不会引起频谱上的变化呢？

询问本科老师得到回复如下：

补零不会真正提高频率分辨率，数据重复变长和多次叠加可能会提高分辨率，但时间开销大了，可以看看数字信号处理。
再者就是在现有数据中插值，用一些有效的插值方法插值把信号变长。
只要插值这些不是非线性变换，理论上不会产生新的频谱。

编写matlab程序，进行尝试。

df=0.1;    %频率分辨率
fs=1000;
N=floor(fs/df)+1;%计算的序列点数
t=0:1/fs:(N-1)/fs;%截取信号的时间段
f=0:df:fs;%功率谱估计的频率分辨率和范围
f=roundn(f,-1);%%find 函数依靠精度识别
n=0:1/fs:1;
% xn=cos(2*pi*40*n)+3*cos(2*pi*100*n)+randn(size(n));
xn=cos(2*pi*40*n)+3*cos(2*pi*100*n);
n0=0:1/fs:10;
xn0=cos(2*pi*40*n0)+3*cos(2*pi*100*n0)+randn(size(n0));


%原始信号
figure
subplot(2,1,1)
plot(xn)
subplot(2,1,2)
Px=abs(fft(xn)).^2/((N/10)^2);%功率谱估计
f1=0:1:fs;
plot(f1(1:150),Px(1:150));
% PxAll(1,:)=Px;


%重复10次
figure
x1=repmat(xn,1,10);
xt1=x1(1,1:size(f,2));
%截取时间段上的离散信号样本序列
%利用周期图法进行功率谱估计，但是其得出的功率谱很不光滑，相应的估计协方差比较大
%增加采样点数也不能使周期图变得更加平滑，这是周期图的缺点，在后面对其改进。
Px1=abs(fft(xt1)).^2/(N^2);%功率谱估计
subplot(2,1,1)
plot(xt1)
subplot(2,1,2)
plot(f(1:1500),Px1(1:1500));
PxAll(2,:)=Px1;


%补充9s的零
figure
x2=[xn,zeros(1,size(f,2)-length(xn))];
xt2=x2(1,1:size(f,2));
Px2=abs(fft(xt2)).^2/((N/10)^2);%功率谱估计
subplot(2,1,1)
plot(xt2)
subplot(2,1,2)
plot(f(1:1500),Px2(1:1500));
PxAll(3,:)=Px2;

分别得到图片如下：

原始信号：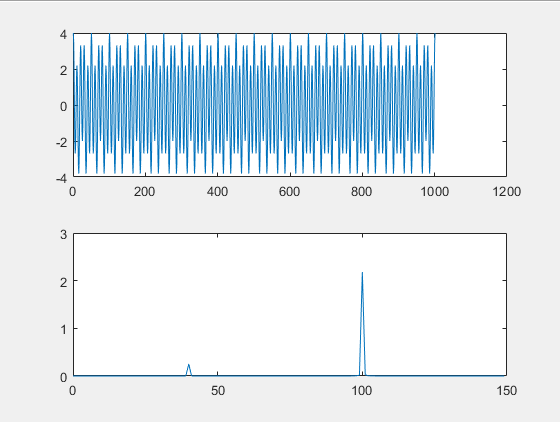

数据重复后：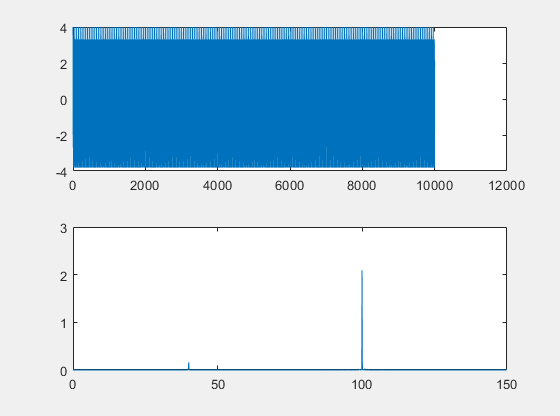

补零后：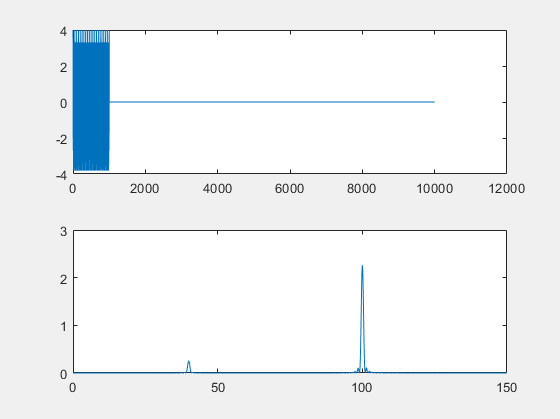

在程序里我设置了xn=cos(2*pi*40*n)+3*cos(2*pi*100*n)，所以频谱应该只包含40、100Hz，而不会在其临近频率有能量，但是原始信号、补零信号得到的频谱上，能量不仅仅分布在40、100Hz两处，认为这是由于频率分辨率不够精细造成的，因此选用数据重复使用方法。

ps：插值法以后再补充。
参考 https://www.zhihu.com/question/30312644

最后

以上就是称心朋友为你收集整理的Matlab 关于补零和延拓来提高FFT分辨率的全部内容，希望文章能够帮你解决Matlab 关于补零和延拓来提高FFT分辨率所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。