【DSP】时域补零与频率分辨率的关系

1. 频率分辨率

频率分辨率是指对两个最近的频谱峰值能够分辨的能力。
一般来说，窗口长度$N$越大，则物理上的频率分辨率越高，其中$N$指的是真实的信号采样点个数，而不是补零之后的长度。频率分辨率可以表示为：
$$\Delta f=\frac{1}{N{T}_s}=\frac{f_s}{N}$$

值得注意的是，补零并不能提高物理上的分辨力。因为补零不能增加数据的有效长度，因而补零不能增加任何信息，不能提高物理意义上的分辨率。

2. 时域补零的好处

1. 频域抽样点数增加，可提高计算上的分辨能力，$N$越大，DFT计算上的分辨能力越高，因此可以克服栅栏效应。
2. 使$N$为2的整数幂，便于FFT计算。

3. 时域补零实验

实验对比了全长76800采样点的原始音频、一帧（1960采样点）音频和分别在前面和后面补零的音频计算fft得到的频谱。
探究以下问题：

1. 时域补零能否增加频率分辨率？
2. 通过补零能否使频谱更接近原始信号的频谱？

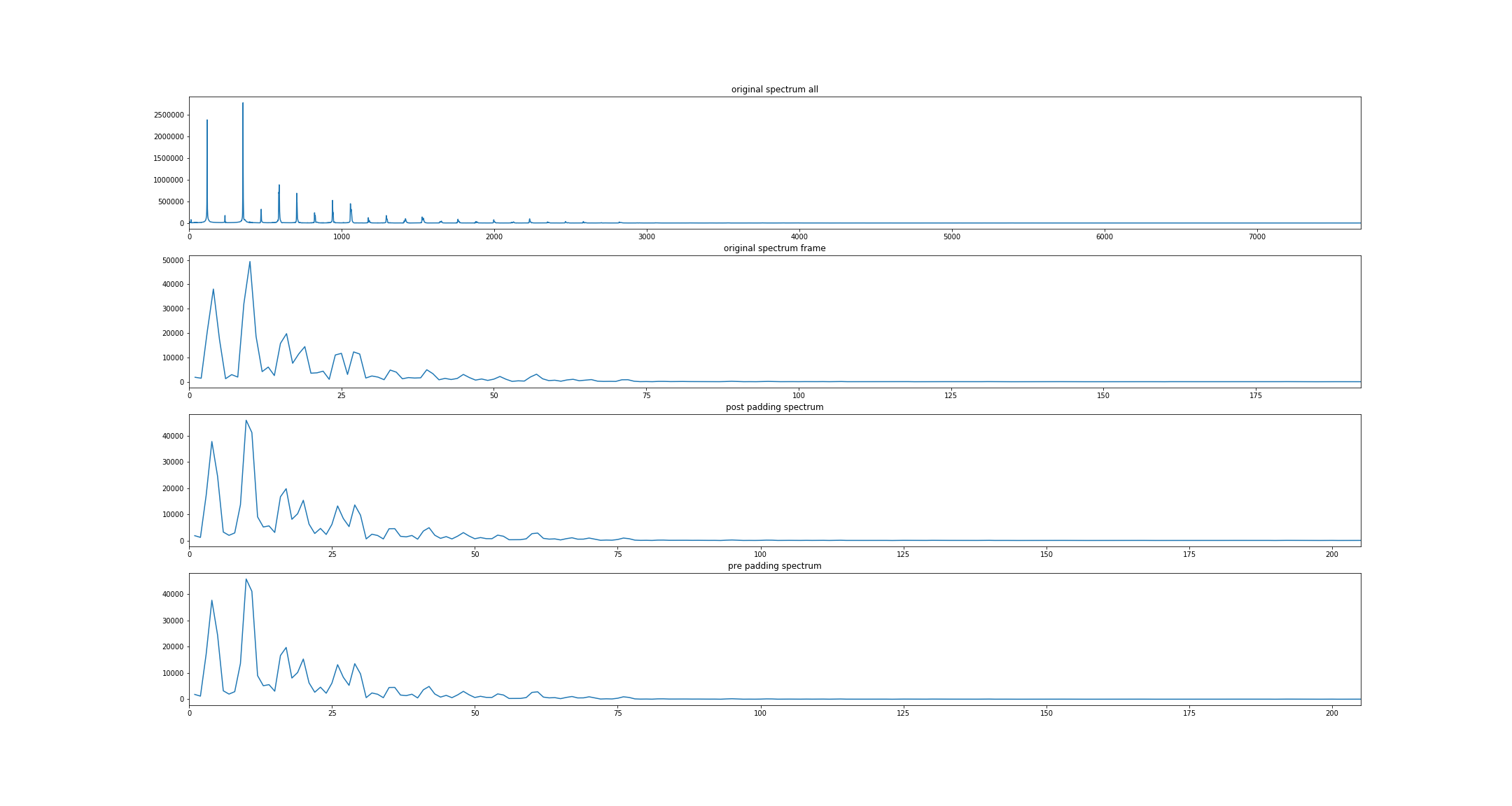
图一：补零后长度为2048采样点

下图第一行为全长76800采样点的原始音频直接做FFT的频谱
第二行为一帧音频（1960采样点）做FFT的频谱
第三行为一帧音频在后面补零后长度为2048采样点得到的频谱
第四行为一帧音频在前面补零后长度为2048采样点得到的频谱

可以看出：
1. 补零到与原帧长差不多的2的整数幂对于提升频谱分辨率没有帮助，仅可方便FFT的计算
2. 在时域前面和后面补零对于计算FFT没有肉眼可见的区别（数值上有细微差别）

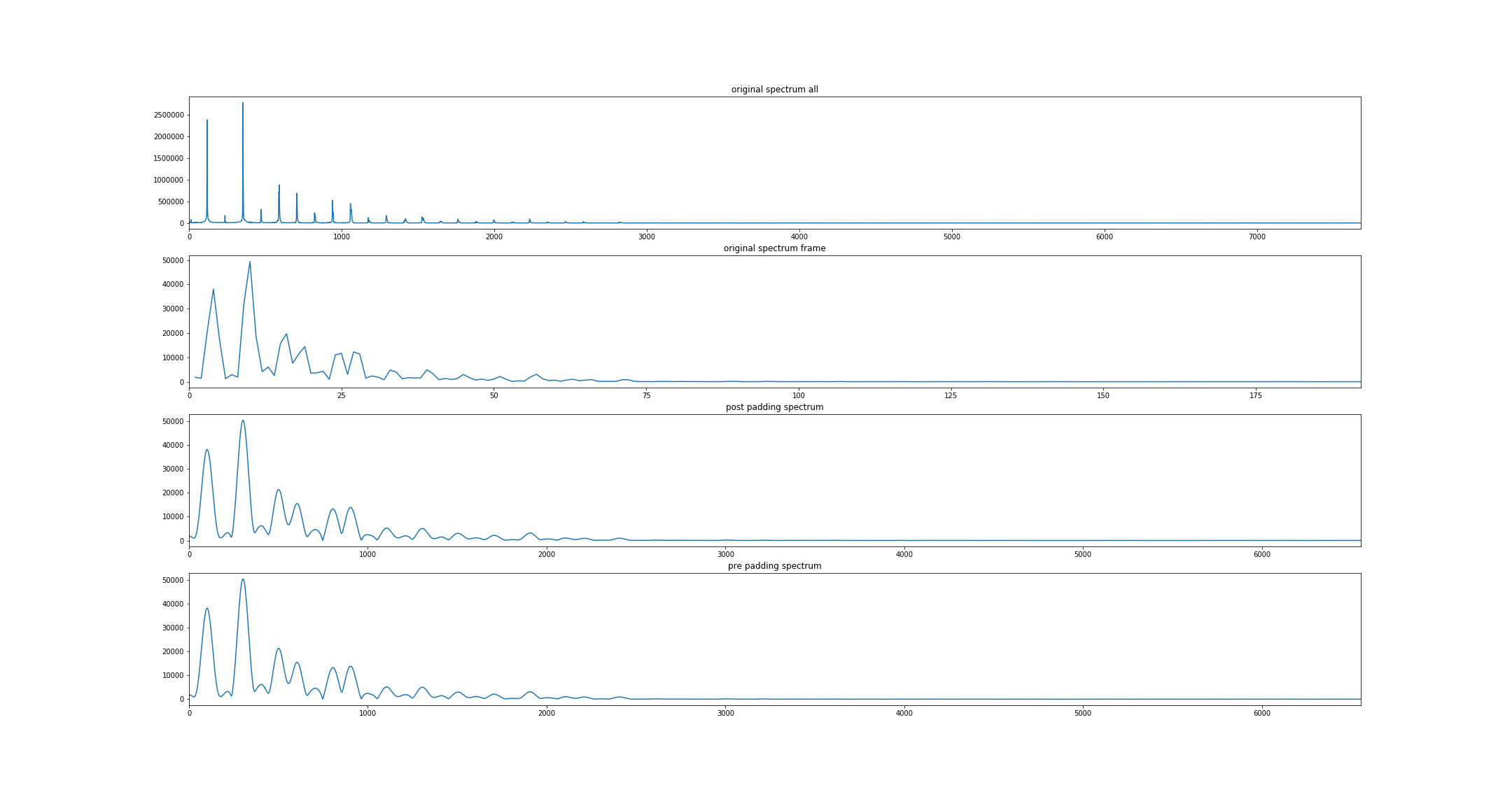
图二：补零后长度为65536采样点（与原始音频长度接近）

下图第一行为全长76800采样点的原始音频直接做FFT的频谱
第二行为一帧音频（1960采样点）做FFT的频谱
第三行为一帧音频在后面补零后长度为65536采样点得到的频谱
第四行为一帧音频在前面补零后长度为65536采样点得到的频谱
可以看出：
补零到与原音频总长差不多的2的整数幂确实使频谱变得更加精细，数值上频率的分辨率也有很大的提高（频谱变得光滑）；但是频谱所展示的信息仍然与未补零的一帧音频差不多，不能恢复出更多原始音频的信息。
因此，我们认为这样的补零在一定程度上可以使一帧音频的频谱更加精细，体现出一些峰值；但是不能认为补零可以提高物理意义上的分辨率，只有增加真实信号的长度才能提高频率分辨率。

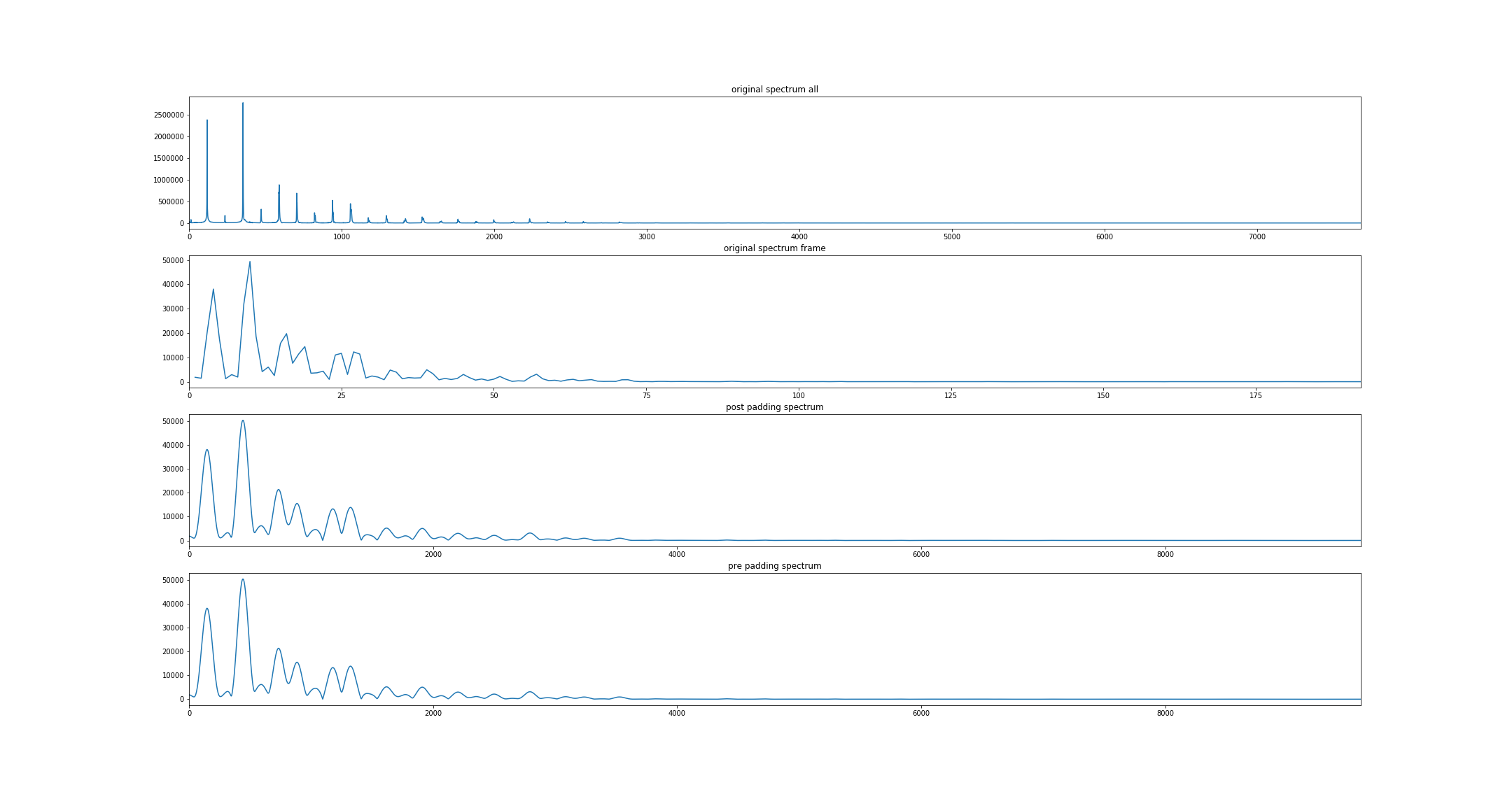
图三：补零长度到96000采样点

想要频率分辨率为1Hz，根据文章开头的公式，则窗口长度需要为96000个采样点。

下图第一行为全长76800采样点的原始音频直接做FFT的频谱
第二行为一帧音频（1960采样点）做FFT的频谱
第三行为一帧音频在后面补零后长度为96000采样点得到的频谱
第四行为一帧音频在前面补零后长度为96000采样点得到的频谱

可以看出：
此时补零的采样点数已经大于了原始信号，但是频谱在直观上与采样点为65536时差不多。从而进一步证明了补零并不能使得分辨率有质的提升，无法接近原始信号的频谱。

4. 小结

• 时域补零可以让频谱更光滑，但不能提高频率分辨率。
• 真实的信号长度越长，物理意义上的频率分辨率越高
• 增加频域抽样点数或者时域补零可以使频域抽样更密，谱线变密后就有可能看到原来看不到的谱分量（减小栅栏效应）
• 在原一帧数据的前面和后面补零没有很大影响

参考文献：

• 《语音信号处理》赵力等
• 《数字信号处理教程》程佩青

最后

以上就是背后火为你收集整理的【DSP】时域补零与频率分辨率的关系的全部内容，希望文章能够帮你解决【DSP】时域补零与频率分辨率的关系所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。