当时在做路径跟踪、路径规划时,使用了MPC,通过项目的应用,对于MPC建立了一定的认识,但是一段时间过去后,认知又渐渐模糊了,当时学习过程中也是看了许多人的blog及代码才弄清楚,这里试图从理论到实践,对MPC进行一次回顾整理。项目为Udacity的MPC课程,详细代码见 https://github.com/wisdom-bob/ipopt_MPC 。
什么是MPC
模型预测控制(Model Predictive Control)指一类算法,周期性基于当帧测量信息在线求解一个有限时间开环优化问题,并将结果的前部分控制序列作用于被控对象。根据所用模型不同,分为动态矩阵控制(DMC),模型算法控制(MAC)、广义预测控制(GPC)。在智能驾驶方向,重点在于基于状态空间模型的模型预测控制。
预测控制最大的吸引力在于它具有显式处理约束的能力, 这种能力来自其基于模型对系统未来动态行为的预测, 通过把约束加到未来的输入、输出或状态变量上, 可以把约束显式表示在一个在线求解的二次规划或非线性规划问题中。
在线求解开环优化问题获得开环优化序列是MPC和传统控制方法的主要区别,因为后者通常是离线求解一个反馈控制律,而该反馈控制律一旦确定,在系统中就不再变动。
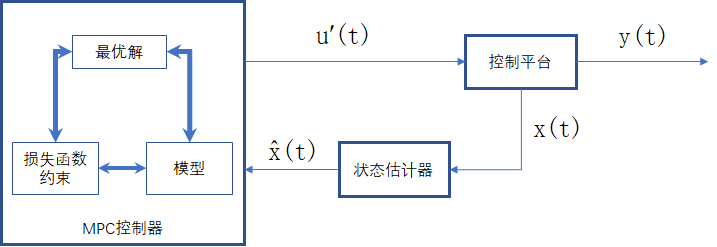
其中,x(t)为t时刻车辆的测量状态量,x*(t)为t时刻车辆的估计状态,u’(t)为t时刻的最优控制解,y(t)为t时刻的系统输出。
MPC算法包括三个步骤:
预测模型:根据历史信息、当前输入预测未来输出。我们需要一个模型能够基于历史信息和当前状态,来预测未来输出,这就涉及状态量的描述,非线性模型的线性化,从而确保预测输出最大限度接近期望值。
滚动优化:某一性能指标最优,反复在线优化。由于外部干扰,模型系统误差等原因,预测输出与实际存在偏差,滚动优化要做的就是找到每个时刻下的局部最优解,一般会设计一个损失函数,转化为二次规划问题,找到最优解。
反馈校正:基于测量对模型预测进行修正。模型基于当前与过去信息预测未来输出,那么未来时刻的输出就是反馈信息,这一部分与模型有较大关系,有些模型把这一部分内容体现在前两步骤中。
下面将根据这三部分,结合代码进行说明,从而更直观的了解如何使用MPC。
问题概述
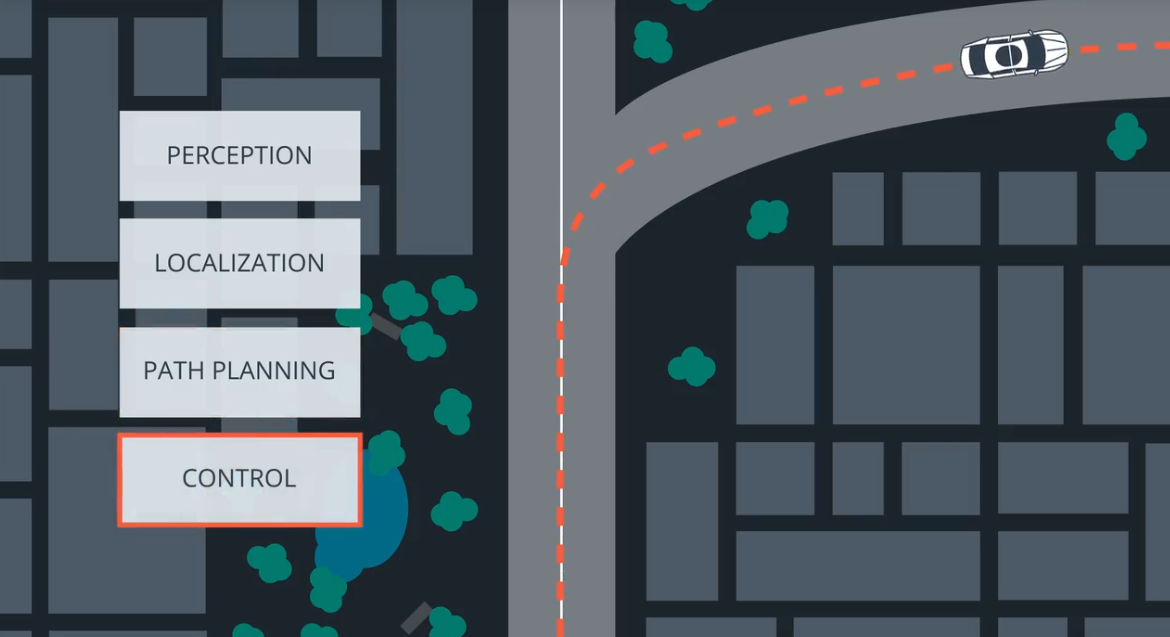
Udacity项目中基于MPC实现行驶轨迹跟踪。控制系统实时接收车辆的状态量(px,py,psi,v)以及前方预行驶航点(ptsx,ptsy),基于以上信息,根据设计的损失函数,基于Cppad的ipopt函数计算出车辆的下面N帧的车辆控制指令。
状态量记录车辆的位置和速度以及相对道路中心线的夹角(具体将在预测模型中讲解)
预行驶航点是经筛选过的行驶航点集,剔除了已走过的航点,一般记录为预行驶的10个航点到20个航点。
预测模型
项目希望基于A*算法实现路径规划,并利用MPC来实现路径跟踪,那么首先摆在面前要解决的问题是如何描述项目中的各个组成部分。
车辆具有多个自由度,运动姿态耦合强,受力复杂,可看做一个非线性多自由度运动刚体,我们希望问题简单化,那么我们就设法简化模型,把模型转化为线性模型。无论是车辆运动学模型,还是车辆动力学模型,皆为非线性系统,而线性模型预测控制较非线性模型预测控制有更好的实时性,且更易于分析和计算,而这对于智能驾驶都非常重要。
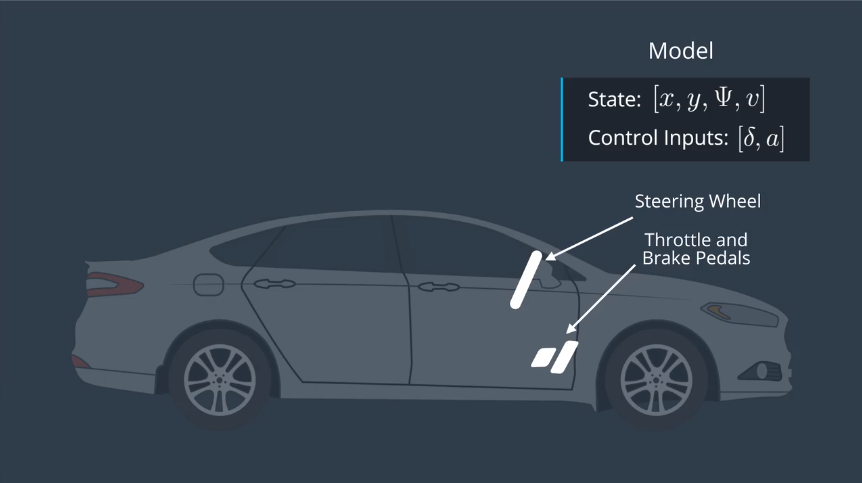
项目采用单车动力学模型和自行车运动学模型,完成对车辆模型的描述。
关于自行车模型这块,详见1,书里面讲的很详细。
自行车动力学模型
动力学模型:简化轮胎力、重力和质量的动力学模型,把车辆的形状简化为自行车结构,把所有的受力集中在前后车轮上。这种简化降低了模型的准确性,但也更易处理,在低速和中速时,运动模型通常近似于实际车辆动力学。
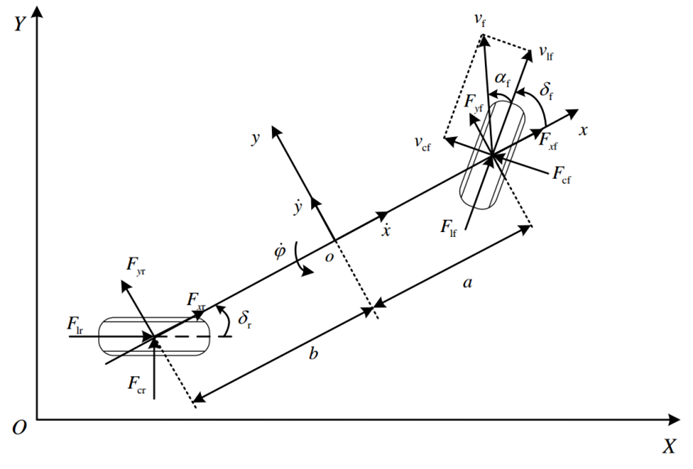
车前轮的方向即是车辆当前的速度方向,在实际车辆运动过程中,当车辆在以相对高的速度行驶时,车轮的方向并不一定车辆当前的速度方向,这个时候,我们引入车辆的动力学自行车模型。
车辆动力学模型通过对轮胎和路面之间的复杂相互作用来描述车辆的运动。在一个动力模型中,我们需要考虑各种各样的力的作用,他们可以大致分为两类:纵向力(Longitudinal force) 和侧向力(Lateral force), 纵向力就是使车辆前后移动的力量,而侧向力则促使车辆在横向移动,在力的相互作用过程中,轮胎起着决定性的作用(根据一定的物理常识,轮胎是车辆运动的一个重要的力的来源)。
由于动力学与控制关系较小,这里只做简单介绍。
自行车运动学模型
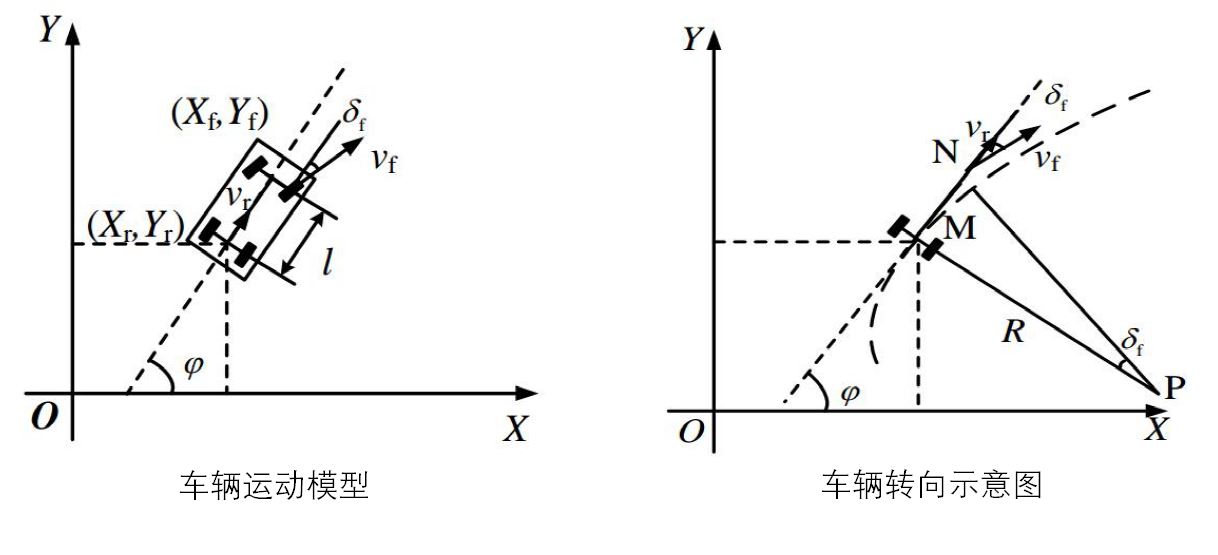
R为后轮转向半径,P为车辆瞬时转动中心,M为车辆后轮轴心,N为前轮轴心。此处,假设转向过程中车辆之心侧偏角保持不变,即车辆瞬时转向半径与道路曲率半径相同。
在后轮行驶轴心(Xr,Yr)处,速度为:
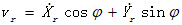
前后轮的运动学约束为:
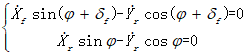
联立可得:
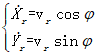
根据前后轮的几何关系可得:
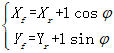
则可以求得横摆角速度为:
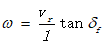
基于横摆角速度和车速,可求出转向半径和前轮偏角:
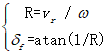
得到车辆运动学模型为:
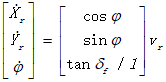
此外我们也不能忽略了模型的物理约束:
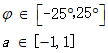
模型整合
车辆模型通过单车模型来表示,而对于整个路径跟踪模型而言,则需要基于单车模型做一些修改。
通过前面介绍,我们知道车辆状态量有(px,py,psi,v),完整模型中又添加了两个量,epsi和cte,用来描述车辆与道路中心线的夹角以及车辆与参考轨迹的横向偏差。
ps.这里实际上道路的描述也并不是常规的笛卡尔坐标系。。
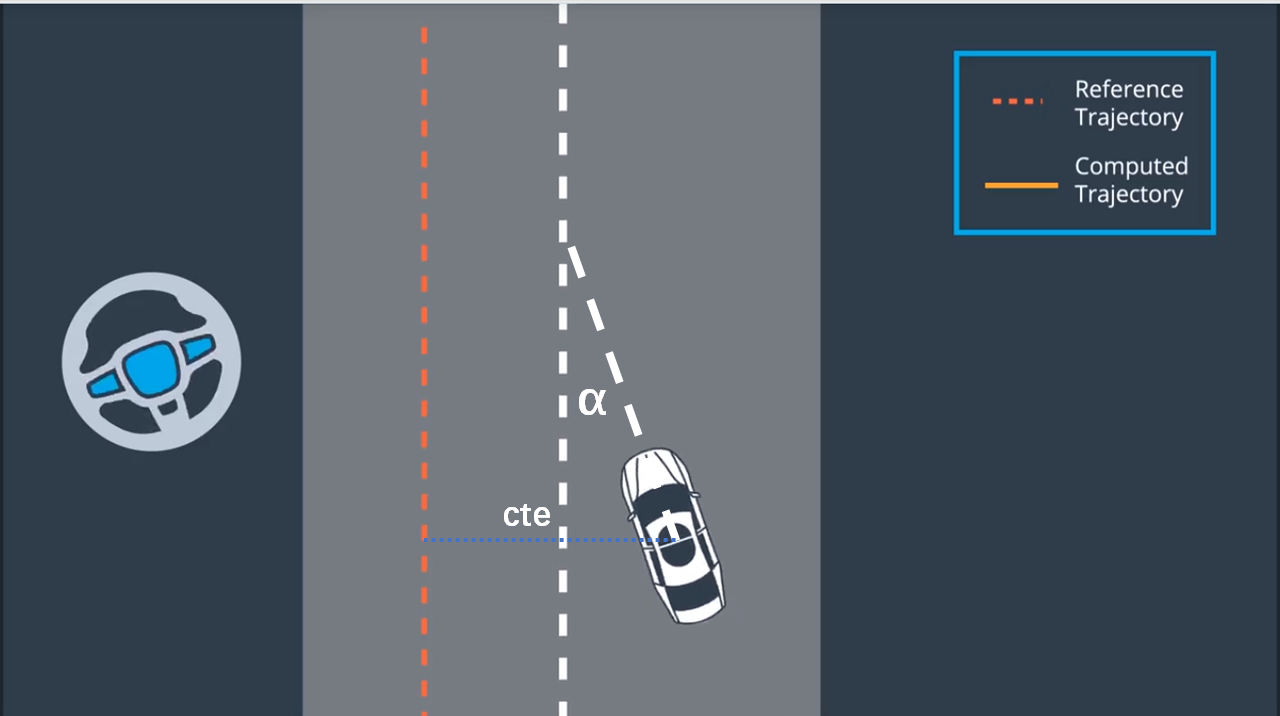
参考轨迹是基于(ptsx,ptsy)的三次多项式拟合曲线表达式f(xt),基于 f(xt) 实时求取横向偏移量cte。
结合以上所有,我们确认的完整模型如下所示:
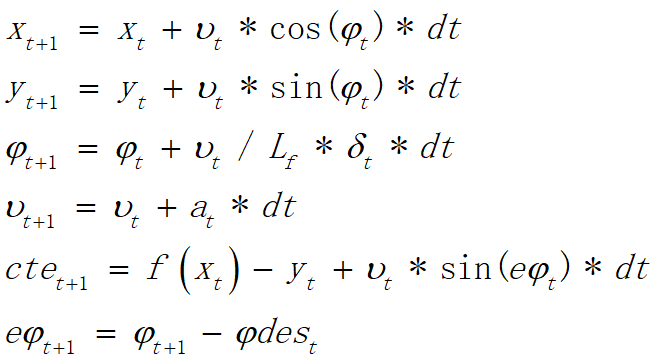
以下结合代码说明输入数据处理。
vector<double> ptsx = j[1]["ptsx"];//世界坐标系预行驶航点x坐标
vector<double> ptsy = j[1]["ptsy"];//世界坐标系预行驶航点y坐标
double px = j[1]["x"];//汽车世界坐标x
double py = j[1]["y"];//汽车世界坐标y
double psi = j[1]["psi"];//航向角
double v = j[1]["speed"];//行驶速度
// 转化世界坐标系航点为车辆坐标系航点
vector<double> waypoints_x;
vector<double> waypoints_y;
for (int i = 0; i < ptsx.size(); i++)
{
double dx = ptsx[i] - px;
double dy = ptsy[i] - py;
waypoints_x.push_back(dx * cos(-psi) - dy * sin(-psi));
waypoints_y.push_back(dx * sin(-psi) + dy * cos(-psi));
}
Eigen::Map<Eigen::VectorXd> waypoints_mx(ptrx, 6);
Eigen::Map<Eigen::VectorXd> waypoints_my(ptry, 6);
// 三次多项式拟合得到预行驶轨迹曲线表达式
Eigen::VectorXd coeffs = polyfit(waypoints_mx, waypoints_my, 3);
double cte = polyeval(coeffs, 0);//当帧车辆行驶偏移量
double epsi = -atan(coeffs[1]); //当帧航向角
滚动优化
滚动优化是求取最优控制解,基于约束,使某一或某些性能指标达到最优实现控制作用。那么设计合适的优化目标函数,就是结果优越性的关键,目标函数的一般形式可表示为状态和控制输入的二次函数:
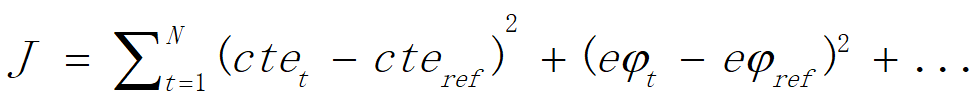
其中,J为损失函数,N为预测时域,cteref,eφref分别为横向偏移量和角度的参考值。
构建损失函数后,还需要设定约束条件:
在项目中,控制输出为[φ,a],即车辆的转向和加速度。
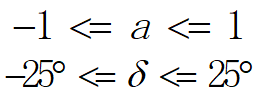
由于约束函数和损失函数的许多参量与整体模型息息相关,这里先对整体模型进行说明。
如图所示为我们目前构建的MPC系统,周期性接受状态量state,输入MPC模型,基于Model,Cost,Constraints计算最优控制解。

基于CppAD的ipopt控制器进行二次规划求解最优解,关于cppad.ipopt详见2。
size_t N = 10;//预测时域
double dt = 0.1;//时间间隔
const double Lf = 2.67;//前半轴距,用于计算航向角
const double ref_cte = 0;//参考横向偏移量
const double ref_epsi= 0;//参考角度
const double ref_v = 100;//参考速度
// 为使用ipopt构建输入数据
size_t x_start = 0;//0~y_start-1
size_t y_start = x_start + N;//y_start~psi_start-1
size_t psi_start = y_start + N;//psi_start ~v_start-1
size_t v_start = psi_start + N;//...
size_t cte_start = v_start + N;
size_t epsi_start = cte_start + N;
size_t delta_start = epsi_start + N;
size_t a_start = delta_start + N - 1;
// fg[]记录所有要求的函数等式,fg[0]嵌入损失函数,fg[>0]嵌入各状态量;
// 同时用lower和upper约束结果,var_bound单独约束fg[0]各参量,constraints约束fg[>0]
// 初始值设定,即当帧检测数据
fg[1 + x_start] = vars[x_start];
fg[1 + y_start] = vars[y_start];
fg[1 + psi_start] = vars[psi_start];
fg[1 + v_start] = vars[v_start];
fg[1 + cte_start] = vars[cte_start];
fg[1 + epsi_start] = vars[epsi_start];
for (int t = 1; t < N; t++) {
AD<double> x1 = vars[x_start + t];
AD<double> x0 = vars[x_start + t - 1];
AD<double> y1 = vars[y_start + t];
AD<double> y0 = vars[y_start + t - 1];
AD<double> psi1 = vars[psi_start + t];
AD<double> psi0 = vars[psi_start + t - 1];
AD<double> v1 = vars[v_start + t];
AD<double> v0 = vars[v_start + t - 1];
AD<double> cte1 = vars[cte_start + t];
AD<double> cte0 = vars[cte_start + t - 1];
AD<double> epsi1 = vars[epsi_start + t];
AD<double> epsi0 = vars[epsi_start + t - 1];
AD<double> a = vars[a_start + t - 1];
AD<double> delta = vars[delta_start + t - 1];
if (t > 1) {
a = vars[a_start + t - 2];
delta = vars[delta_start + t - 2];
}
AD<double> f0 = coeffs[0] + coeffs[1] * x0 + coeffs[2] * CppAD::pow(x0, 2) + coeffs[3] * CppAD::pow(x0, 3);
AD<double> psides0 = CppAD::atan(coeffs[1] + 2 * coeffs[2] * x0 + 3 * coeffs[3] * CppAD::pow(x0, 2));
fg[1 + x_start + t] = x1 - (x0 + v0 * CppAD::cos(psi0) * dt);
fg[1 + y_start + t] = y1 - (y0 + v0 * CppAD::sin(psi0) * dt);
fg[1 + psi_start + t] = psi1 - (psi0 - v0/Lf * delta * dt);
fg[1 + v_start + t] = v1 - (v0 + a * dt);
fg[1 + cte_start + t] = cte1 - ((f0 - y0) + (v0 * CppAD::sin(epsi0) * dt));
fg[1 + epsi_start + t] = epsi1 - ((psi0 - psides0) - v0/Lf * delta * dt);
}
Dvector vars(n_vars);
for (int i = 0; i < n_vars; i++)
vars[i] = 0;
vars[x_start] = x;
vars[y_start] = y;
vars[psi_start] = psi;
vars[v_start] = v;
vars[cte_start] = cte;
vars[epsi_start] = epsi;
构造代价函数与约束
构建代价函数,与深度学习的损失函数是一个意思,我们想要输出满足什么要求,越重要的参数权重越大,反之依然,甚至不约束。
注意!
平方是为了统一符号,权重差异不能过于悬殊,本身数据间存在量纲差异,既然没有进行归一化处理,那就特别注意权重间的权衡。下面根据优先级排列损失函数的参数:
a. 横向偏移误差,指实际轨迹点与参考轨迹点间的距离;
b. 速度误差,指实际速度与期望速度的差;
c. 角度偏移量,指航向角与参考值的差异;
d. 刹车/油门调节量,目的是为了保证刹车/油门变化的平稳性;
e.航向角变化率,相邻时间间隔的航向角变化量;
f.加速度变化量,描述相邻时间间隔,加速度的变化快慢。
ps.具体权重只有调试才能完全确定,编码见代码。
// fg[0]挂载损失函数值
for (uint i = 0; i < N; i++) {
fg[0] += 2500*CppAD::pow(vars[cte_start + i] - ref_cte, 2);
fg[0] += 2500*CppAD::pow(vars[epsi_start + i] - ref_epsi, 2);
fg[0] += CppAD::pow(vars[v_start + i] - ref_v, 2);
}
for (uint i = 0; i < N - 1; i++) {
fg[0] += 5*CppAD::pow(vars[delta_start + i], 2);
fg[0] += 100*CppAD::pow(vars[a_start + i], 2);
fg[0] += 700*CppAD::pow(vars[delta_start + i] * vars[v_start+i], 2);
}
for (int i = 0; i < N - 2; i++) {
fg[0] += 200*CppAD::pow(vars[delta_start + i + 1] - vars[delta_start + i], 2);
fg[0] += 10*CppAD::pow(vars[a_start + i + 1] - vars[a_start + i], 2);
}
设定了损失函数,车辆已经能够计算出可行的结果,但结果的可行性却还有待考究,这就需要约束条件来表现了。
约束条件有两个作用:
1.确保结果的实际可行性,满足损失函数最小的最优解不一定模型能够执行,而加上约束,结果就一定是在车辆模型执行范围内的结果。
2.约束条件缩小了状态空间范围,二次规划等最优解算法往往需要反复递归迭代得出结果,状态空间越小,计算时间也将缩减。
在项目中,可以考虑的约束条件有如下:
a. 最大前轮转角
b. 最大刹车/油门调节量
ps.在损失函数中已约束参量,不再重复约束,另外一些约束是针对等式而设定的,详见代码。
//6个state量,N为预测时域,delta和a各N-1个,为输出控制数量
size_t n_vars = N * 6 + (N - 1) * 2;
size_t n_constraints = N * 6;
//记录约束的最小值和最大值,对应fg[0]损失函数的各参量的约束
Dvector vars_lowerbound(n_vars);
Dvector vars_upperbound(n_vars);
for (int i = 0; i < delta_start; i++) {
vars_lowerbound[i] = -1.0e19;//除了a和delta其他量无约束
vars_upperbound[i] = 1.0e19; //值域为(-inf,inf)
}
for (int i = delta_start; i < a_start; i++) {
vars_lowerbound[i] = -0.436332;//delta约束为角度制下
vars_upperbound[i] = 0.436332; //(-25,25)
}
for (int i = a_start; i < n_vars; i++) {
vars_lowerbound[i] = -1.0;//a约束为(-1,1)
vars_upperbound[i] = 1.0;
}
// 设置约束的最短值和最小值,约束fg[i]的值域限制,i!=0
Dvector constraints_lowerbound(n_constraints);
Dvector constraints_upperbound(n_constraints);
for (int i = 0; i < n_constraints; i++) {
constraints_lowerbound[i] = 0;// lower和upper=0,代表fg[i]嵌入为等式
constraints_upperbound[i] = 0;
}
constraints_lowerbound[x_start] = x;//嵌入为常数,则upper=lower
constraints_lowerbound[y_start] = y;
constraints_lowerbound[psi_start] = psi;
constraints_lowerbound[v_start] = v;
constraints_lowerbound[cte_start] = cte;
constraints_lowerbound[epsi_start] = epsi;
constraints_upperbound[x_start] = x;
constraints_upperbound[y_start] = y;
constraints_upperbound[psi_start] = psi;
constraints_upperbound[v_start] = v;
constraints_upperbound[cte_start] = cte;
constraints_upperbound[epsi_start] = epsi;
以上完成对模型参量的约束,输出结果的约束,损失函数的构建,只需要调用求解器CppAD::ipopt::solve,即可求出结果。详见代码 https://github.com/wisdom-bob/ipopt_MPC 。
FG_eval fg_eval(coeffs);// a class for cost function and model
std::string options="";//NULL
CppAD::ipopt::solve_result<Dvector> solution;
CppAD::ipopt::solve<Dvector, FG_eval>(
options, vars, vars_lowerbound, vars_upperbound, constraints_lowerbound,
constraints_upperbound, fg_eval, solution);
// Check some of the solution values
ok &= solution.status == CppAD::ipopt::solve_result<Dvector>::success;
// Cost
auto cost = solution.obj_value;
std::cout << "Cost " << cost << std::endl;
vector<double> result;
result.push_back(solution.x[delta_start]);
result.push_back(solution.x[a_start]);
for (int i = 0; i < N-1; i++) {
result.push_back(solution.x[x_start + i + 1]);
result.push_back(solution.x[y_start + i + 1]);
}
return result;
反馈矫正
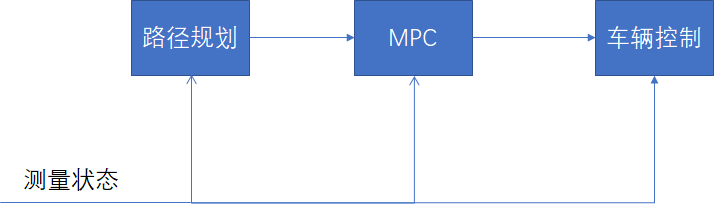
MPC本质上还是一种反馈控制,当我们通过最优化方法得到一组控制输出后(本例中就是未来10步的控制输出),车辆执行控制指令,同时继续以一定的频率接收到表示当前车辆的状态 [px,py,v,psi,cte,epsi]。这个状态会被同时输入到路径规划模块以及MPC控制模块,路径规划模块会依据新的车辆状态,结合感知模块的信息以及地图信息重新做出规划。MPC则根据新的参考路径和车辆当前状态进行新一轮的预测控制。需要注意的是,车辆真实状态的反馈并不是一个预测时间段的控制执行完以后才反馈的,反馈的时间间隔往往小于一个预测时间段(在本例中,预测时间段为 0.1×10=1s)。
项目整理总结
以上基于MPC的整体架构进行思路讲解和代码说明,但是结构太生硬,不易理解。下面进行思路整理,这里参考了较多这位博主的思路3。
我们希望车辆按照我们的参考路线行驶,设定时间间隔dt=0.1s,选取10个dt,那么根据预测模型,我们可以预测车辆在未来1s的状态(准确的说是每个时间间隔的状态)。
要求解这样一个最优化问题,首先依据神经网络优化方式设计损失函数,把车辆参考速度、车辆与参考路线偏移量、车辆航向角、车辆加速度等量以加权平方形式都考虑进来;
此外设计最优化问题的变量约束,如车辆航向角转角theta、加速度a的取值范围。基于输入,求解带约束的最优化问题,得到控制输出。
要注意的是车辆执行延迟问题。已知车辆执行延迟为100ms,即在指令发出时,模型预测的第一步实际上在制动延迟的时间内,车辆执行上状态指令。本文中模型采用10步预测,每步间隔为100ms,为让模型更贴近实际,我们约束这一步控制指令,即(a,deltaf)为上一状态的指令,这样,我们的模型预测控制就将制动延迟考虑了进来。
MPC的一般工作步骤可以概括如下:
0、基于事件信息构建预测模型,并基于模型约束和输出需求,设计损失及约束函数;
1、结合历史信息、当前状态以及预测模型,计算最优控制解,预测N步的系统输出;
2、输出执行;
3、等待下一周期,获取检测信息,重复步骤1、2、3。
关于Cppad::ipopt算法核心可见内点法
现明确算法使用内点法,而内点法解法主要分为障碍函数法和对偶内点法,这里对障碍函数法做一个简单说明:
##已知线性约束和非线性约束,以及要求最优化式子->等式约束、不等式约束、损失函数,
##那么基于约束,我们可以很容易得到关于最优化式子的拉格朗日乘子式(把约束转化为各乘子)
##障碍函数法的关键在于对于不等式约束提出了一种障碍函数,构建阻碍拉格朗日乘子:
##综上所示,最后得到拉格朗日乘子式如下所示
此时,基于牛顿下降法,经过多次迭代后取得目标最优解。
https://download.csdn.net/download/uxux007/10345011 ↩︎
http://coin-or.github.io/CppAD/doc/ipopt_solve_get_started.cpp.htm ↩︎
https://blog.csdn.net/AdamShan/article/details/79083755 ↩︎
最后
以上就是孤独山水最近收集整理的关于自动驾驶——模型预测控制(MPC)理解与实践什么是MPC的全部内容,更多相关自动驾驶——模型预测控制(MPC)理解与实践什么是MPC内容请搜索靠谱客的其他文章。
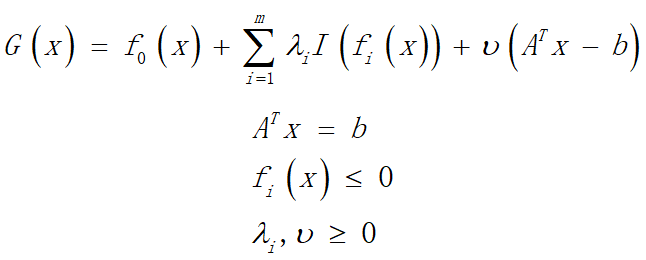








发表评论 取消回复