MPC 控制原理
- 1 生活中的启示
- 2 实际控制的例子
- 参考文献
Yin 机械工程师
本文引自 一个模型预测控制(MPC)的简单实现.
1 生活中的启示
情景如下:你们团队每天早晨开一次例会,主要会议内容是你汇报工作进度,领导根据工作目标和工作进度,制定当天的工作计划,你领到工作计划后开始工作。每天都这样周而复始,从领导的角度看,这件工作实现了“闭环”,工作进度“可控”,这就是闭环控制系统。

不同的领导(控制器)水平有高又低,按照介绍控制器先踩一脚PID的国际惯例,设:

则PID控制器的控制律为:
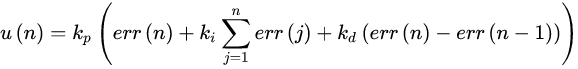
从该控制律中我们可以看到PID的两个问题:
1, PID控制器不具有“前瞻性”:参与计算的各个量,有当前的 [公式] ,上个控制周期的 [公式] ,以及之前所有的 [公式] 累计和,偏偏没有未来的 [公式] 。这个“领导”目光过于短浅,只求今天能完成任务,哪怕第二天公司就倒闭了,那也是第二天要解决的麻烦,今天该干啥干啥。
2, PID属于无模型控制。作为一个“领导”,PID仅仅通过工作目标和工作进度上的差距,以及三个近乎魔法般的数字,就制定了工作计划,完全不考虑你的工作能力和这项工作的难度,这是非常失职的。
为了提高工作的的可行性,经过思考,我们还可以有另一种方案:
- 领导听完你的汇报后,根据工作进度(系统状态)、工作目标(参考值)、你的工作能力和任务难度(系统模型),制定了未来10天的工作计划,每一天要干什么都写得清清楚楚明明白白。
- 领导将这十天计划里面第一天的计划交给你,剩下九天的计划销毁。
- 第二天重复上述过程。
显然第二种方案更具有可行性,它能根据任务的完成情况及时调整工作计划,同时兼顾了未来的工作计划、你的工作能力和任务的难度,更符合我们的认知。
当然这种方案还有一点小缺陷,比如“剩下九天计划销毁”,领导看了这个方案肯定心里不舒服,辛辛苦苦做的计划凭什么销毁呢?为了弥补这个缺陷,我们提出了“控制时域”和“预测时域”的概念。控制时域是指领导做多少天的计划,预测时域是指领导思考多长远的进度。比如,领导考虑到计划跟不上变化,想太长远没意义,就先做了五天的计划(控制时域是五天),然后第6-10天的计划和第5天的计划一模一样,领导预测了下按照这样的十天计划,十天后进度完成的还算可以(预测时域是十天)。这样依然给你第一天的计划,销毁剩下九天的计划,领导的工作量却少了许多。
模型预测控制的基本思想就蕴含在上述过程中,它利用一个已有的模型、系统当前的状态和未来的控制量,来预测系统未来的输出,然后与我们期望的系统输出做比较,得到一个损失函数,即:
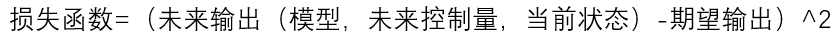
由于上式中模型、当前状态、期望输出都是已知的,因此只有未来控制量一个自变量。采用二次规划的方法求解出某个未来控制量,使得损失函数最小,这个未来控制量的第一个元素就是当前控制周期的控制量。
2 实际控制的例子
2.1 问题描述
在无限光滑的一维水平直线上有一个质量为 [公式] 的滑块,初始位置与初始速度都为0,现需要设计控制器,在传感器测得滑块位置 [公式] 的基础上,为滑块提供外力 [u] ,使其跟随参考点 [x]
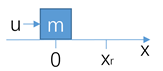
2.2 预测模型
首先建立动力学方程:
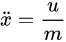
选取状态向量 (除非特殊说明,后文中x表示状态向量,而不是滑块位置),构建系统状态方程为:
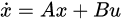
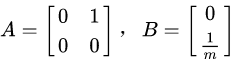
2.3 预测模型离散化
采用前向欧拉法将状态方程离散化:
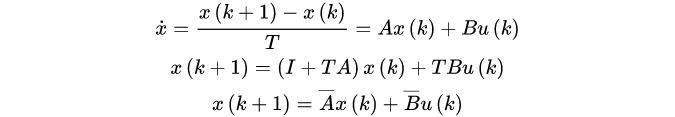
其中
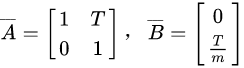
,T为控制周期。
省略一些,全是数学公式
2.6 仿真
对于2.1中例子的动力学方程:
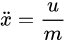
两边同时拉普拉斯变换:
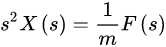
可得传递函数:
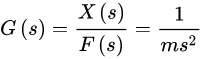
在simulink中搭建仿真环境如图4,并编写MPC控制器:
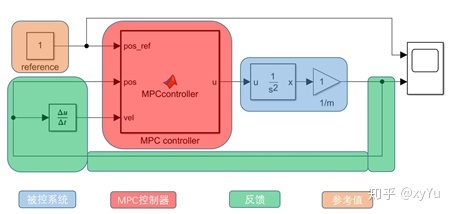
function u = MPCcontroller(pos_ref, pos, vel)
%参数设置
m = 1.05; %滑块质量,增加了5%作为建模误差
T = 0.01; %控制周期10ms
p = 45; %控制时域(预测时域)
Q = 10*eye(2*p); %状态误差权重
W = 0.0001*eye(p); %控制输出权重
umax = 100; %控制量限制,即最大的力
Rk = zeros(2*p,1); %参考值序列
Rk(1:2:end) = pos_ref;%参考位置由函数参数指定
Rk(2:2:end) = vel; %参考速度跟随实际速度
%构建中间变量
xk = [pos;vel]; %xk
A_ = [1 T;0 1]; %离散化预测模型参数A
B_ = [0;T/m]; %离散化预测模型参数B
psi = zeros(2*p,2); %psi
for i=1:1:p
psi(i*2-1:i*2,1:2)=A_^i;
end
theta = zeros(2*p,p); %theta
for i=1:1:p
for j=1:1:i
theta(i*2-1:i*2,j)=A_^(i-j)*B_;
end
end
E = psi*xk-Rk; %E
H = 2*(theta'*Q*theta+W); %H
f = (2*E'*Q*theta)'; %f
%优化求解
coder.extrinsic('quadprog');
Uk=quadprog(H,f,[],[],[],[],-umax,umax);
%返回控制量序列第一个值
u = 0.0; %指定u的类型
u = Uk(1); %提取控制序列第一项
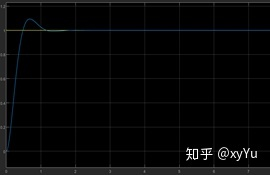 p=40,仿真结果
p=40,仿真结果
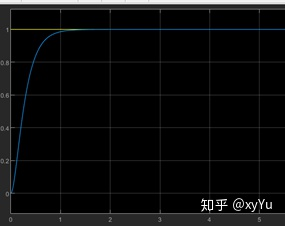
p=60,仿真结果
参考文献
陈虹. 模型预测控制[M]. 科学出版社, 2013.
龚建伟, 姜岩, 徐威. 无人驾驶车辆模型预测控制[M]. 北京理工大学出版社, 2014.
MPC 控制原理
最后
以上就是阔达酸奶最近收集整理的关于MPC 控制原理1 生活中的启示2 实际控制的例子参考文献的全部内容,更多相关MPC内容请搜索靠谱客的其他文章。








发表评论 取消回复