1.高通滤波器
首先，对一副图像进行如下二维傅里叶变换。
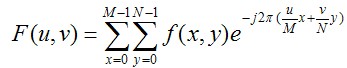
我们将u=0和v=0带上式，我们可以得到如下式子。
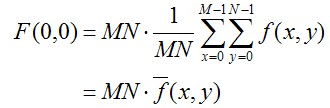
根据上式，可以到F(0,0)的值是非常大的。这里，我们将
F(0,0)称为直流分量，直流分量比其他的成分要大好几个数量级。所以，这也就是傅里叶谱为什么需要使用对数变换才能看清楚的原因。
这里，对于高通滤波器而言，由于直流分量被衰减，所以，所得到的图像的动态范围是非常狭窄的，也就造成了图像偏灰。进一步而言，保持直流（DC）分量，对别的部分进行增幅，可以增强图像的细节。这样的滤波器称为锐化滤波器。这一小节主要介绍高通滤波器与锐化滤波器。
1.1理想高通滤波器
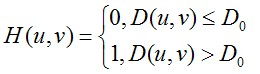
这里的D0是滤波器的阻带半径，而D(u,v)是点到滤波器中央的距离。理想高通的滤波器的振幅特性如下所示。
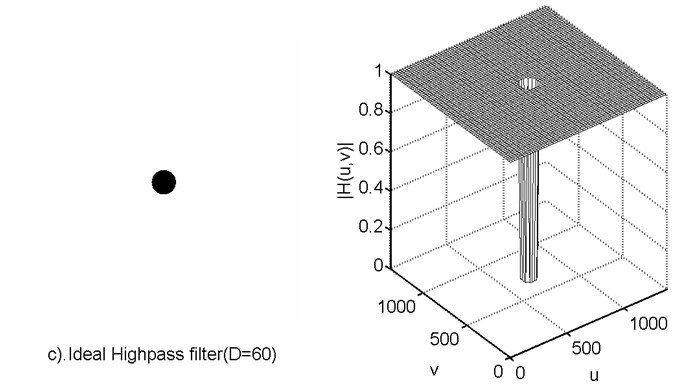
用这个滤波器对图像进行处理，可得到如下所示的结果。我们可以看到，与理想的低通滤波器一样，所得到的图像有很明显的振铃现象。结果图像从视觉上来看，有些偏暗，这是因为图像的直流分量被滤掉的原因。
1.2巴特沃斯高通滤波器
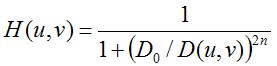
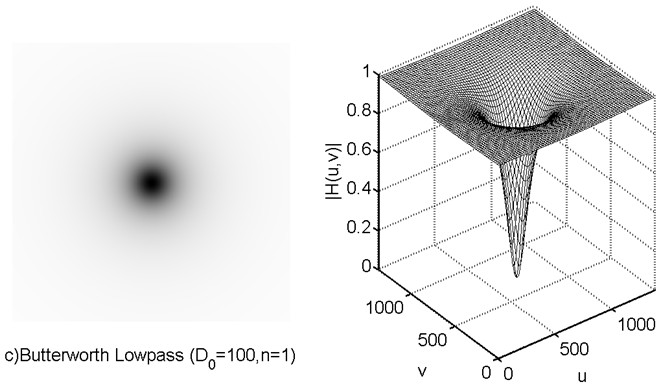
同样的，巴特沃斯高通滤波器也可以通过改变次数n，对过度特性进行调整。过大的n会造成振铃现象。
1.3高斯高通滤波器
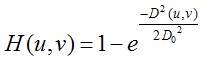
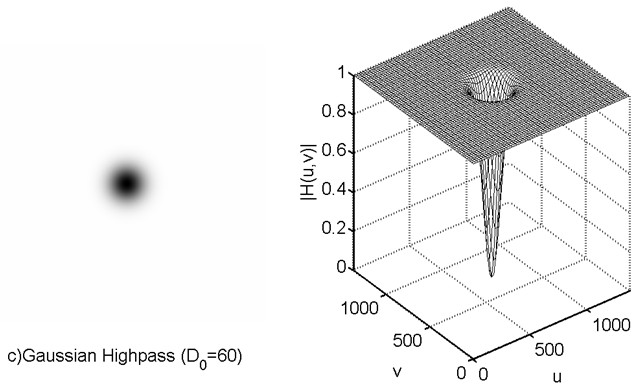
高斯滤波器的过度特性很好，所以不会发生振铃现象。
1.4 上述三种滤波器的实现Matlab代码
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299close all; clear all; %% ---------Ideal Highpass Filters (Fre. Domain)------------ f = imread('characters_test_pattern.tif'); f = mat2gray(f,[0 255]); [M,N] = size(f); P = 2*M; Q = 2*N; fc = zeros(M,N); for x = 1:1:M for y = 1:1:N fc(x,y) = f(x,y) * (-1)^(x+y); end end F = fft2(fc,P,Q); H_1 = ones(P,Q); H_2 = ones(P,Q); for x = (-P/2):1:(P/2)-1 for y = (-Q/2):1:(Q/2)-1 D = (x^2 + y^2)^(0.5); if(D <= 60) H_1(x+(P/2)+1,y+(Q/2)+1) = 0; end if(D <= 160) H_2(x+(P/2)+1,y+(Q/2)+1) = 0; end end end G_1 = H_1 .* F; G_2 = H_2 .* F; g_1 = real(ifft2(G_1)); g_1 = g_1(1:1:M,1:1:N); g_2 = real(ifft2(G_2)); g_2 = g_2(1:1:M,1:1:N); for x = 1:1:M for y = 1:1:N g_1(x,y) = g_1(x,y) * (-1)^(x+y); g_2(x,y) = g_2(x,y) * (-1)^(x+y); end end %% -----show------- figure(); subplot(1,2,1); imshow(f,[0 1]); xlabel('a).Original Image'); subplot(1,2,2); imshow(log(1 + abs(F)),[ ]); xlabel('b).Fourier spectrum of a'); figure(); subplot(1,2,1); imshow(H_1,[0 1]); xlabel('c).Ideal Highpass filter(D=60)'); subplot(1,2,2); h = mesh(1:20:P,1:20:Q,H_1(1:20:P,1:20:Q)); set(h,'EdgeColor','k'); axis([0 P 0 Q 0 1]); xlabel('u');ylabel('v'); zlabel('|H(u,v)|'); figure(); subplot(1,2,1); imshow(log(1 + abs(G_1)),[ ]); xlabel('d).Result of filtering using c'); subplot(1,2,2); imshow(g_1,[0 1]); xlabel('e).Result image'); figure(); subplot(1,2,1); imshow(H_2,[0 1]); xlabel('f).Ideal Highpass filter(D=160)'); subplot(1,2,2); h = mesh(1:20:P,1:20:Q,H_2(1:20:P,1:20:Q)); set(h,'EdgeColor','k'); axis([0 P 0 Q 0 1]); xlabel('u');ylabel('v'); zlabel('|H(u,v)|'); figure(); subplot(1,2,1); imshow(log(1 + abs(G_2)),[ ]); xlabel('g).Result of filtering using e'); subplot(1,2,2); imshow(g_2,[0 1]); xlabel('h).Result image'); close all; clear all; %% ---------Butterworth Highpass Filters (Fre. Domain)------------ f = imread('characters_test_pattern.tif'); f = mat2gray(f,[0 255]); [M,N] = size(f); P = 2*M; Q = 2*N; fc = zeros(M,N); for x = 1:1:M for y = 1:1:N fc(x,y) = f(x,y) * (-1)^(x+y); end end F = fft2(fc,P,Q); H_1 = zeros(P,Q); H_2 = zeros(P,Q); for x = (-P/2):1:(P/2)-1 for y = (-Q/2):1:(Q/2)-1 D = (x^2 + y^2)^(0.5); D_0 = 100; H_1(x+(P/2)+1,y+(Q/2)+1) = 1/(1+(D_0/D)^2); H_2(x+(P/2)+1,y+(Q/2)+1) = 1/(1+(D_0/D)^6); end end G_1 = H_1 .* F; G_2 = H_2 .* F; g_1 = real(ifft2(G_1)); g_1 = g_1(1:1:M,1:1:N); g_2 = real(ifft2(G_2)); g_2 = g_2(1:1:M,1:1:N); for x = 1:1:M for y = 1:1:N g_1(x,y) = g_1(x,y) * (-1)^(x+y); g_2(x,y) = g_2(x,y) * (-1)^(x+y); end end %% -----show------- figure(); subplot(1,2,1); imshow(f,[0 1]); xlabel('a).Original Image'); subplot(1,2,2); imshow(log(1 + abs(F)),[ ]); xlabel('b).Fourier spectrum of a'); figure(); subplot(1,2,1); imshow(H_1,[0 1]); xlabel('c)Butterworth Lowpass (D_{0}=100,n=1)'); subplot(1,2,2); h = mesh(1:20:P,1:20:Q,H_1(1:20:P,1:20:Q)); set(h,'EdgeColor','k'); axis([0 P 0 Q 0 1]); xlabel('u');ylabel('v'); zlabel('|H(u,v)|'); figure(); subplot(1,2,1); imshow(log(1 + abs(G_1)),[ ]); xlabel('d).Result of filtering using c'); subplot(1,2,2); imshow(g_1,[0 1]); xlabel('e).Result image'); figure(); subplot(1,2,1); imshow(H_2,[0 1]); xlabel('f).Butterworth Lowpass (D_{0}=100,n=3)'); subplot(1,2,2); h = mesh(1:20:P,1:20:Q,H_2(1:20:P,1:20:Q)); set(h,'EdgeColor','k'); axis([0 P 0 Q 0 1]); xlabel('u');ylabel('v'); zlabel('|H(u,v)|'); figure(); subplot(1,2,1); imshow(log(1 + abs(G_2)),[ ]); xlabel('g).Result of filtering using e'); subplot(1,2,2); imshow(g_2,[0 1]); xlabel('h).Result image'); close all; clear all; %% ---------Gaussian Highpass Filters (Fre. Domain)------------ f = imread('characters_test_pattern.tif'); f = mat2gray(f,[0 255]); [M,N] = size(f); P = 2*M; Q = 2*N; fc = zeros(M,N); for x = 1:1:M for y = 1:1:N fc(x,y) = f(x,y) * (-1)^(x+y); end end F = fft2(fc,P,Q); H_1 = zeros(P,Q); H_2 = zeros(P,Q); for x = (-P/2):1:(P/2)-1 for y = (-Q/2):1:(Q/2)-1 D = (x^2 + y^2)^(0.5); D_0 = 60; H_1(x+(P/2)+1,y+(Q/2)+1) = 1 - exp(-(D*D)/(2*D_0*D_0)); D_0 = 160; H_2(x+(P/2)+1,y+(Q/2)+1) = 1 - exp(-(D*D)/(2*D_0*D_0)); end end G_1 = H_1 .* F; G_2 = H_2 .* F; g_1 = real(ifft2(G_1)); g_1 = g_1(1:1:M,1:1:N); g_2 = real(ifft2(G_2)); g_2 = g_2(1:1:M,1:1:N); for x = 1:1:M for y = 1:1:N g_1(x,y) = g_1(x,y) * (-1)^(x+y); g_2(x,y) = g_2(x,y) * (-1)^(x+y); end end %% -----show------- figure(); subplot(1,2,1); imshow(f,[0 1]); xlabel('a).Original Image'); subplot(1,2,2); imshow(log(1 + abs(F)),[ ]); xlabel('b).Fourier spectrum of a'); figure(); subplot(1,2,1); imshow(H_1,[0 1]); xlabel('c)Gaussian Highpass (D_{0}=60)'); subplot(1,2,2); h = mesh(1:20:P,1:20:Q,H_1(1:20:P,1:20:Q)); set(h,'EdgeColor','k'); axis([0 P 0 Q 0 1]); xlabel('u');ylabel('v'); zlabel('|H(u,v)|'); figure(); subplot(1,2,1); imshow(log(1 + abs(G_1)),[ ]); xlabel('d).Result of filtering using c'); subplot(1,2,2); imshow(g_1,[0 1]); xlabel('e).Result image'); figure(); subplot(1,2,1); imshow(H_2,[0 1]); xlabel('f).Gaussian Highpass (D_{0}=160)'); subplot(1,2,2); h = mesh(1:20:P,1:20:Q,H_2(1:20:P,1:20:Q)); set(h,'EdgeColor','k'); axis([0 P 0 Q 0 1]); xlabel('u');ylabel('v'); zlabel('|H(u,v)|'); figure(); subplot(1,2,1); imshow(log(1 + abs(G_2)),[ ]); xlabel('g).Result of filtering using e'); subplot(1,2,2); imshow(g_2,[0 1]); xlabel('h).Result image');
1.5 锐化滤波器
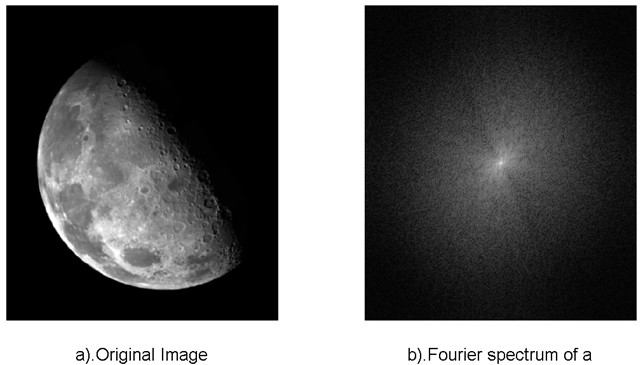
按照之前所说的，锐化滤波器是将傅里叶谱的直流分量保留，然后将其余的成分增幅。使用锐化滤波器，可以对图像的细节进行增强，使得细节凸显出来。锐化滤波器的表达式如下所示。
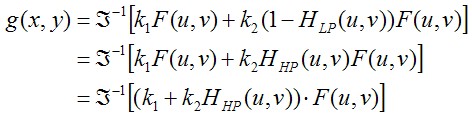
其实上式的目的很明显，就是先将原图的傅里叶
谱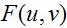
保留下来，然后叠加上高通滤波器的结果
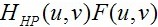，所得到的图像就是锐化后的图像了。这里为了调整锐化程度，引入了两个变量
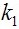与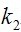
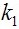。可以调整直流分量的衰减程度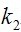，可以调整高频分量的增幅程度。
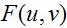保留下来，然后叠加上高通滤波器的结果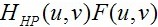，所得到的图像就是锐化后的图像了。这里为了调整锐化程度，引入了两个变量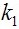与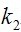。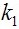可以调整直流分量的衰减程度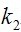，可以调整高频分量的增幅程度。
下面是代码。
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79close all; clear all; clc; %% ---------The High-Fre-Emphasis Filters (Fre. Domain)------------ f = imread('blurry_moon.tif'); f = mat2gray(f,[0 255]); [M,N] = size(f); P = 2*M; Q = 2*N; fc = zeros(M,N); for x = 1:1:M for y = 1:1:N fc(x,y) = f(x,y) * (-1)^(x+y); end end F = fft2(fc,P,Q); H_HP = zeros(P,Q); for x = (-P/2):1:(P/2)-1 for y = (-Q/2):1:(Q/2)-1 D = (x^2 + y^2)^(0.5); D_0 = 80; H_HP(x+(P/2)+1,y+(Q/2)+1) = 1 - exp(-(D*D)/(2*D_0*D_0)); end end G_HP = H_HP .* F; G_HFE = (1 + 1.1 * H_HP) .* F; g_1 = real(ifft2(G_HP)); g_1 = g_1(1:1:M,1:1:N); g_2 = real(ifft2(G_HFE)); g_2 = g_2(1:1:M,1:1:N); for x = 1:1:M for y = 1:1:N g_1(x,y) = g_1(x,y) * (-1)^(x+y); g_2(x,y) = g_2(x,y) * (-1)^(x+y); end end g = histeq(g_2); %g_1 = mat2gray(g_1); %% -----show------- figure(); subplot(1,2,1); imshow(f,[0 1]); xlabel('a).Original Image'); subplot(1,2,2); imshow(log(1 + abs(F)),[ ]); xlabel('b).Fourier spectrum of a'); figure(); subplot(1,2,1); imshow(g_1,[0 1]); xlabel('c).Result image of High-pass Filter'); subplot(1,2,2); imshow(log(1 + abs(G_HP)),[ ]); xlabel('d).Result of filtering using e'); figure(); subplot(1,2,1); imshow(g_2,[0 1]); 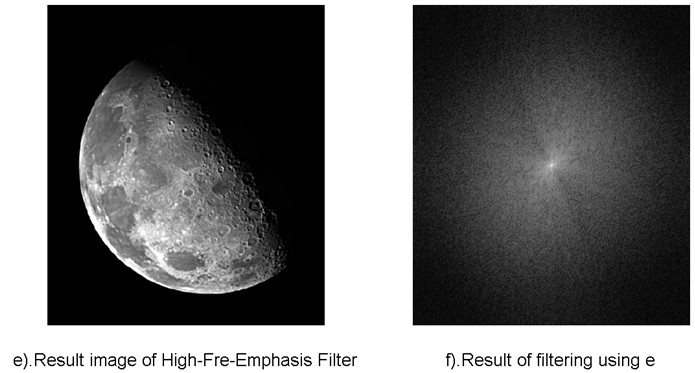xlabel('e).Result image of High-Fre-Emphasis Filter'); subplot(1,2,2); imshow(log(1 + abs(G_HFE)),[ ]); xlabel('f).Result of filtering using e');
2.带阻滤波器
同样的，带阻滤波器也有三种特性。高斯、巴特沃斯和理想，三种类型，其数学表达式如下所示。
其带通滤波器可以使用上面的表格转化而得。
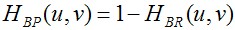
带阻滤波器可以用于去除周期性噪声，为了体现带阻滤波器的特性，我们先对一幅图像增加很严重的噪声。
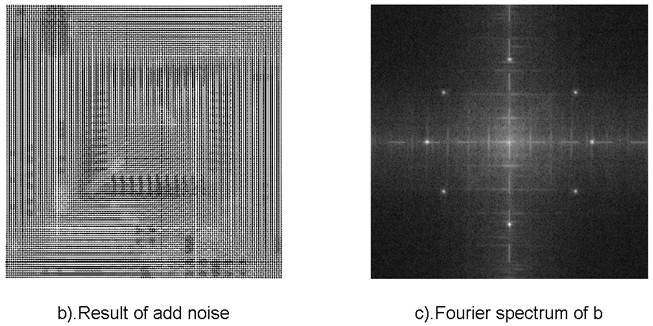
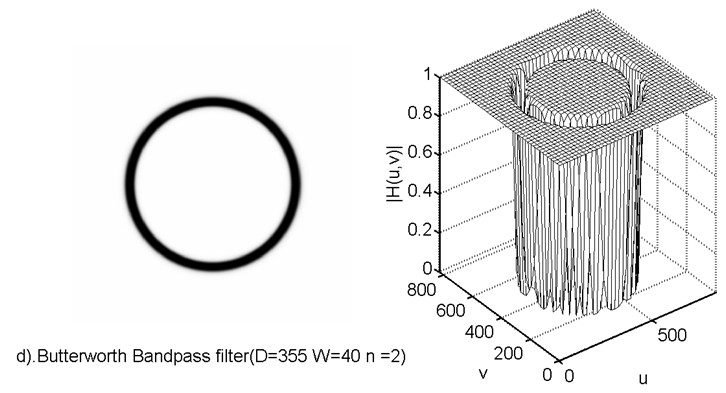
在原图的傅里叶谱上添加了几个很明显的亮点。在对其做IDFT，可以看到，原图被严重的周期噪声污染了。此时，我们可以使用带阻滤波器，可以有很好的去噪效果。为了避免振铃现象，选择使用如下所示巴特沃斯带阻滤波器，所用滤波器的次数为2次。使用空间域的操作，要去除这种噪声基本是不可能的，这也是频域内的操作的优点。
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135close all; clear all; clc; %% ---------------------Add Noise------------------------- f = imread('left.tif'); f = mat2gray(f,[0 255]); [M,N] = size(f); P = 2*M; Q = 2*N; fc = zeros(M,N); for x = 1:1:M for y = 1:1:N fc(x,y) = f(x,y) * (-1)^(x+y); end end F = fft2(fc,P,Q); H_NP = ones(P,Q); for x = (-P/2):1:(P/2)-1 for y = (-Q/2):1:(Q/2)-1 D = 2; v_k = -200; u_k = 150; D_k = ((x+u_k)^2 + (y+v_k)^2)^(0.5); H_NP(x+(P/2)+1,y+(Q/2)+1) = H_NP(x+(P/2)+1,y+(Q/2)+1) * 1/(1+(D/D_k)^4); D_k = ((x-u_k)^2 + (y-v_k)^2)^(0.5); H_NP(x+(P/2)+1,y+(Q/2)+1) = H_NP(x+(P/2)+1,y+(Q/2)+1) * 1/(1+(D/D_k)^4); v_k = 200; u_k = 150; D_k = ((x+u_k)^2 + (y+v_k)^2)^(0.5); H_NP(x+(P/2)+1,y+(Q/2)+1) = H_NP(x+(P/2)+1,y+(Q/2)+1) * 1/(1+(D/D_k)^4); D_k = ((x-u_k)^2 + (y-v_k)^2)^(0.5); H_NP(x+(P/2)+1,y+(Q/2)+1) = H_NP(x+(P/2)+1,y+(Q/2)+1) * 1/(1+(D/D_k)^4); v_k = 0; u_k = 250; D_k = ((x+u_k)^2 + (y+v_k)^2)^(0.5); H_NP(x+(P/2)+1,y+(Q/2)+1) = H_NP(x+(P/2)+1,y+(Q/2)+1) * 1/(1+(D/D_k)^4); D_k = ((x-u_k)^2 + (y-v_k)^2)^(0.5); H_NP(x+(P/2)+1,y+(Q/2)+1) = H_NP(x+(P/2)+1,y+(Q/2)+1) * 1/(1+(D/D_k)^4); v_k = 250; u_k = 0; D_k = ((x+u_k)^2 + (y+v_k)^2)^(0.5); H_NP(x+(P/2)+1,y+(Q/2)+1) = H_NP(x+(P/2)+1,y+(Q/2)+1) * 1/(1+(D/D_k)^4); D_k = ((x-u_k)^2 + (y-v_k)^2)^(0.5); H_NP(x+(P/2)+1,y+(Q/2)+1) = H_NP(x+(P/2)+1,y+(Q/2)+1) * 1/(1+(D/D_k)^4); H_NP(x+(P/2)+1,y+(Q/2)+1) = 1 + 700*(1 - H_NP(x+(P/2)+1,y+(Q/2)+1)); end end G_Noise = F .* H_NP; g_noise = real(ifft2(G_Noise)); g_noise = g_noise(1:1:M,1:1:N); for x = 1:1:M for y = 1:1:N g_noise(x,y) = g_noise(x,y) * (-1)^(x+y); end end %% ---------Bondpass Filters (Fre. Domain)------------ H_1 = ones(P,Q); for x = (-P/2):1:(P/2)-1 for y = (-Q/2):1:(Q/2)-1 D = (x^2 + y^2)^(0.5); D_0 = 250; W = 30; H_1(x+(P/2)+1,y+(Q/2)+1) = 1/(1+((D*W)/((D*D) - (D_0*D_0)))^6); end end G_1 = H_1 .* G_Noise; g_1 = real(ifft2(G_1)); g_1 = g_1(1:1:M,1:1:N); for x = 1:1:M for y = 1:1:N g_1(x,y) = g_1(x,y) * (-1)^(x+y); end end %% -----show------- close all; figure(); subplot(1,2,1); imshow(f,[0 1]); xlabel('a).Original Image'); subplot(1,2,2); imshow(log(1 + abs(F)),[ ]); xlabel('b).Fourier spectrum of a'); figure(); subplot(1,2,2); imshow(log(1 + abs(G_Noise)),[ ]); xlabel('c).Fourier spectrum of b'); subplot(1,2,1); imshow(g_noise,[0 1]); xlabel('b).Result of add noise'); figure(); subplot(1,2,1); imshow(H_1,[0 1]); 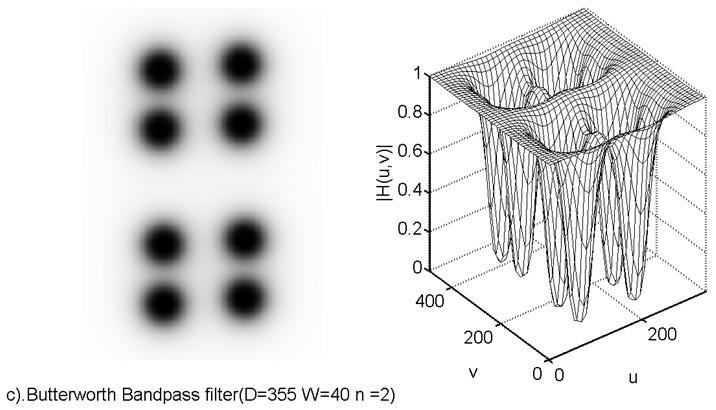xlabel('d).Butterworth Bandpass filter(D=355 W=40 n =2)'); subplot(1,2,2); h = mesh(1:20:Q,1:20:P,H_1(1:20:P,1:20:Q)); set(h,'EdgeColor','k'); axis([0 Q 0 P 0 1]); xlabel('u');ylabel('v'); zlabel('|H(u,v)|'); figure(); subplot(1,2,2); imshow(log(1 + abs(G_1)),[ ]); xlabel('e).Fourier spectrum of f'); subplot(1,2,1); imshow(g_1,[0 1]); xlabel('f).Result of denoise');
3.陷波滤波器(Notch Filter)
陷波滤波器也用于去除周期噪声，虽然带阻滤波器也能可以去除周期噪声，但是带阻滤波器对噪声以外的成分也有衰减。而陷波滤波器主要对，某个点进行衰减，对其余的成分不损失。使用下图将更容易理解。
从空间域内看，图像存在着周期性噪声。其傅里叶频谱中，也能看到噪声的所在之处(这里我用红圈标注出来了，他们不是数据的一部分)。我们如果使用带阻滤波器的话，是非常麻烦的，也会使得图像有损失。陷波滤波器，能够直接对噪声处进行衰减，可以有很好的去噪效果。
其表达式如下所示，陷波滤波器可以通过对高通滤波器的中心，进行位移就可以得到了。
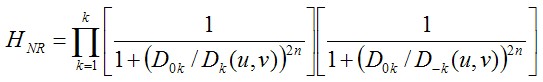
这里，由于傅里叶的周期性，傅里叶频谱上不可能单独存在一个点的噪声，必定是关于远点对称的一个噪声对。这里的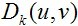
与
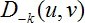需要去除的噪声点，其求取的方式如下所示。
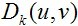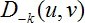与需要去除的噪声点，其求取的方式如下所示。
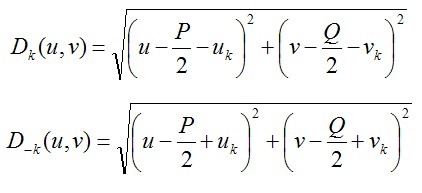
针对于上图，我们设计如下滤波器，去进行去噪。
（图片下标错了，后续更新改过来！）
所得到的结果，如下所示。噪声已经被去除了，画质得到了很大的改善。
（图片下标错了，后续更新改过来！）
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97close all; clear all; clc; %% ---------Butterworth Notch filter (Fre. Domain)------------ f = imread('car_75DPI_Moire.tif'); f = mat2gray(f,[0 255]); [M,N] = size(f); P = 2*M; Q = 2*N; fc = zeros(M,N); for x = 1:1:M for y = 1:1:N fc(x,y) = f(x,y) * (-1)^(x+y); end end F = fft2(fc,P,Q); H_NF = ones(P,Q); for x = (-P/2):1:(P/2)-1 for y = (-Q/2):1:(Q/2)-1 D = 30; v_k = 59; u_k = 77; D_k = ((x+u_k)^2 + (y+v_k)^2)^(0.5); H_NF(x+(P/2)+1,y+(Q/2)+1) = H_NF(x+(P/2)+1,y+(Q/2)+1) * 1/(1+(D/D_k)^4); D_k = ((x-u_k)^2 + (y-v_k)^2)^(0.5); H_NF(x+(P/2)+1,y+(Q/2)+1) = H_NF(x+(P/2)+1,y+(Q/2)+1) * 1/(1+(D/D_k)^4); v_k = 59; u_k = 159; D_k = ((x+u_k)^2 + (y+v_k)^2)^(0.5); H_NF(x+(P/2)+1,y+(Q/2)+1) = H_NF(x+(P/2)+1,y+(Q/2)+1) * 1/(1+(D/D_k)^4); D_k = ((x-u_k)^2 + (y-v_k)^2)^(0.5); H_NF(x+(P/2)+1,y+(Q/2)+1) = H_NF(x+(P/2)+1,y+(Q/2)+1) * 1/(1+(D/D_k)^4); v_k = -54; u_k = 84; D_k = ((x+u_k)^2 + (y+v_k)^2)^(0.5); H_NF(x+(P/2)+1,y+(Q/2)+1) = H_NF(x+(P/2)+1,y+(Q/2)+1) * 1/(1+(D/D_k)^4); D_k = ((x-u_k)^2 + (y-v_k)^2)^(0.5); H_NF(x+(P/2)+1,y+(Q/2)+1) = H_NF(x+(P/2)+1,y+(Q/2)+1) * 1/(1+(D/D_k)^4); v_k = -54; u_k = 167; D_k = ((x+u_k)^2 + (y+v_k)^2)^(0.5); H_NF(x+(P/2)+1,y+(Q/2)+1) = H_NF(x+(P/2)+1,y+(Q/2)+1) * 1/(1+(D/D_k)^4); D_k = ((x-u_k)^2 + (y-v_k)^2)^(0.5); H_NF(x+(P/2)+1,y+(Q/2)+1) = H_NF(x+(P/2)+1,y+(Q/2)+1) * 1/(1+(D/D_k)^4); end end G_1 = H_NF .* F; g_1 = real(ifft2(G_1)); g_1 = g_1(1:1:M,1:1:N); for x = 1:1:M for y = 1:1:N g_1(x,y) = g_1(x,y) * (-1)^(x+y); end end %% -----show------- close all; figure(); subplot(1,2,1); imshow(f,[0 1]); xlabel('a).Original Image'); subplot(1,2,2); imshow(log(1 + abs(F)),[ ]); xlabel('b).Fourier spectrum of a'); figure(); subplot(1,2,1); imshow(H_NF,[0 1]); xlabel('c).Butterworth Notch filter(D=30 n=2)'); subplot(1,2,2); h = mesh(1:10:Q,1:10:P,H_NF(1:10:P,1:10:Q)); set(h,'EdgeColor','k'); axis([0 Q 0 P 0 1]); xlabel('u');ylabel('v'); zlabel('|H(u,v)|'); figure(); subplot(1,2,2); imshow(log(1 + abs(G_1)),[ ]); xlabel('e).Fourier spectrum of d'); subplot(1,2,1); imshow(g_1,[0 1]); xlabel('d).Result image');
原文发于
博客：
http://blog.csdn.net/thnh169/
最后
以上就是活力万宝路最近收集整理的关于[数字图像处理]频域滤波(2)--高通滤波器，带阻滤波器与陷波滤波器的全部内容，更多相关[数字图像处理]频域滤波(2)--高通滤波器内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
![[数字图像处理]频域滤波(2)--高通滤波器，带阻滤波器与陷波滤波器](/uploads/reation/bcimg5.png)
发表评论 取消回复