三种高通滤波器（理想高通 巴特沃斯高通 高斯高通）及拉普拉斯增强算子的时域图像
1、理想高通滤波器
图像
D0 = 30
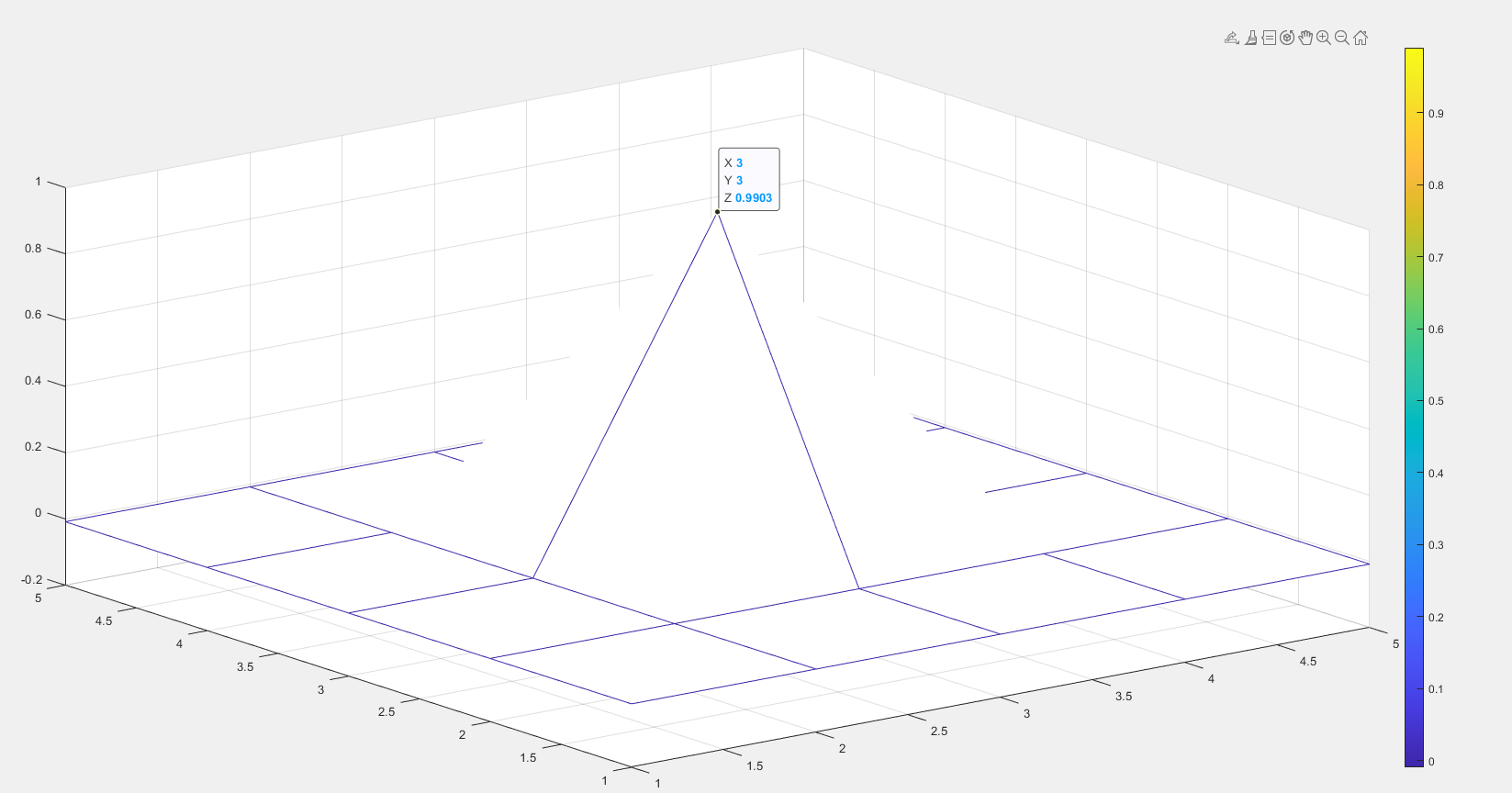
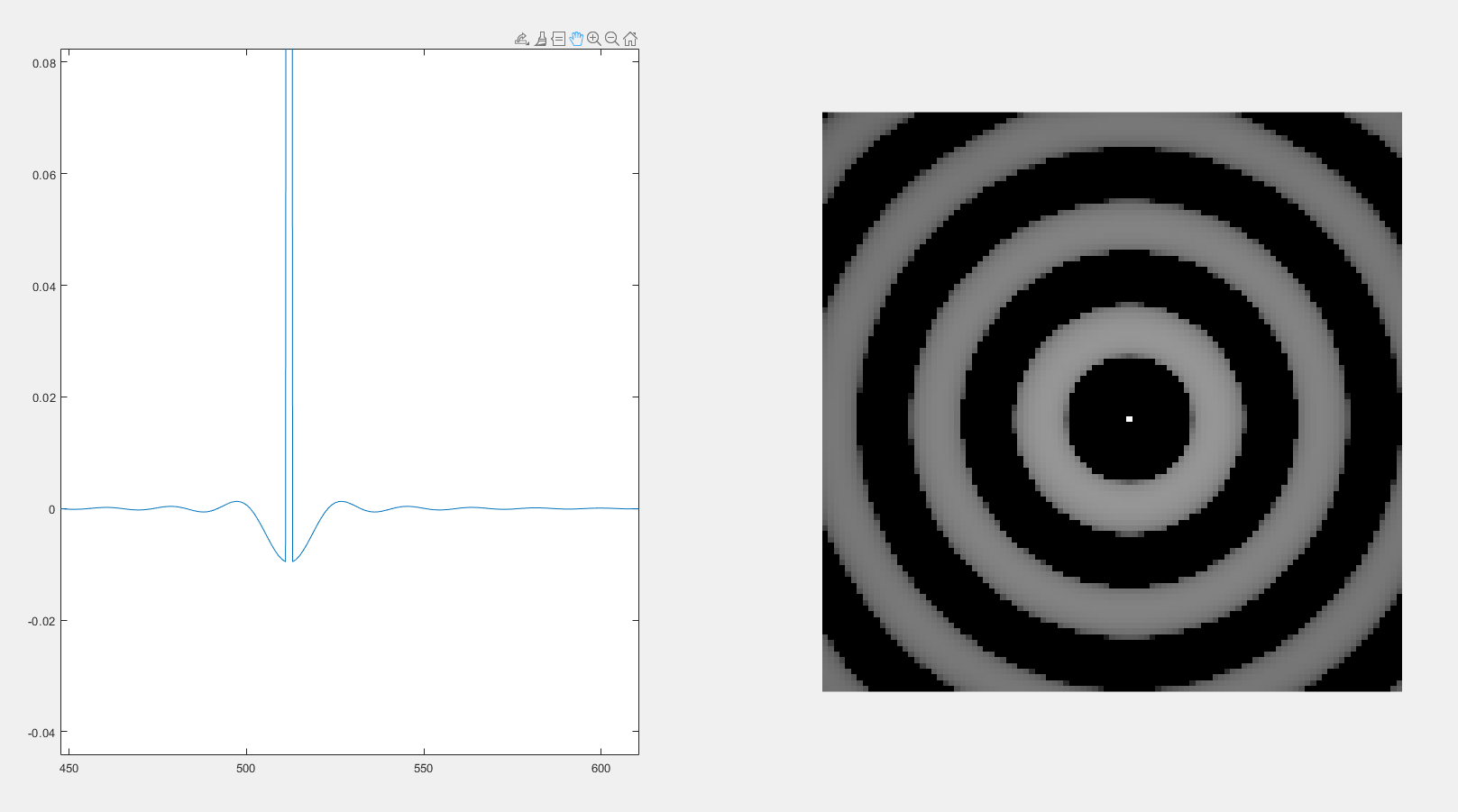
D0= 80
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52clear close all %输入半径参数 D0 = [30 80]; Di = 2; %图像预处理（归一化及填充） aIn = imread("Moon.jpg"); aDouble = double(aIn); a1Double = aDouble/max(max(aDouble)); [ra,ca] = size(aIn); maxL = max(ra,ca); n = 1; while(maxL>2^n) n = n+1; end aFill = zeros(2^n,2^n); aFill(1:ra,1:ca) = a1Double; %提取处理后图像大小，进行滤波器的制作 [Ra,Ca] = size(aFill); [X,Y] = meshgrid(0:Ra-1,0:Ca-1); %更改此部分可以更换D0的值 r = D0(Di)*(Ra/ra); %制作滤波器 Duv = ((X+1)-round(Ra/2)).^2+((Y+1)-round(Ca/2)).^2; Duv(Duv<=r.^2) = 0; Duv(Duv~=0) = 1; Huv = Duv.*(-1).^(X+Y); %将滤波器从频域变换到空域观察 ifi = real(ifft2(Huv)); ifiXY = ifi.*(-1).^(X+Y); %w控制滤波器中心输出框大小并输出 w = 2; HxyOut = ifiXY(Ra/2+1-w:Ra/2+1+w,Ca/2+1-w:Ca/2+1+w); figure, mesh(HxyOut) colorbar %显示空域中滤波器形状（剖线及二维图） xianshi = ifiXY(460:560,460:560).*10000000; xianshi(xianshi<0) = 0; x = 0:1023; y = ifiXY(513,:); figure, subplot(121),plot(x,y); subplot(122),imshow(log(xianshi+1),[]);
分析
随着D0（理想高通滤波器半径）的增大，振铃更加明显且密集（理想滤波器的振铃不可能消除）。
随着D0（理想滤波器半径）增大时，中心点变暗。
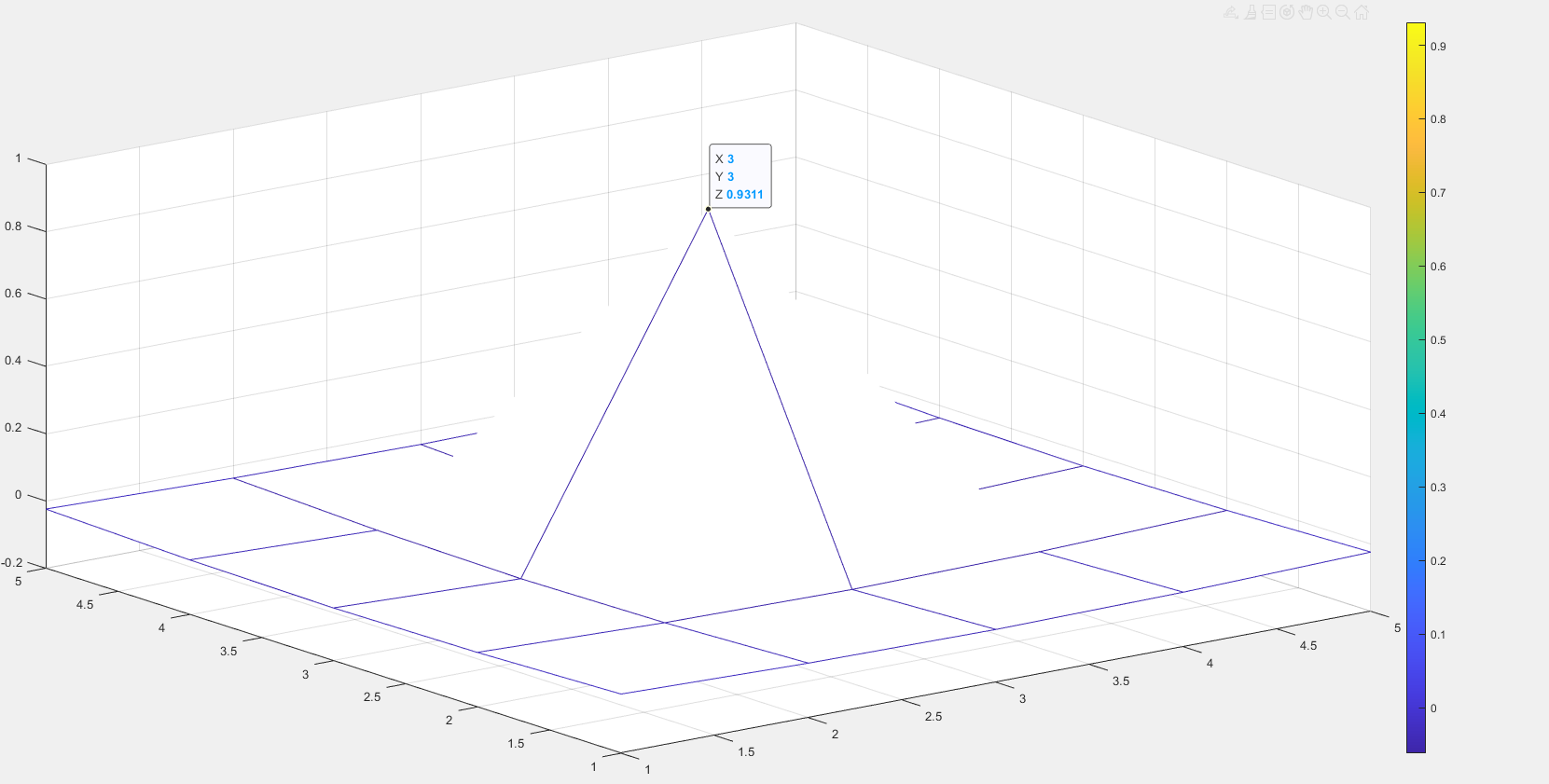
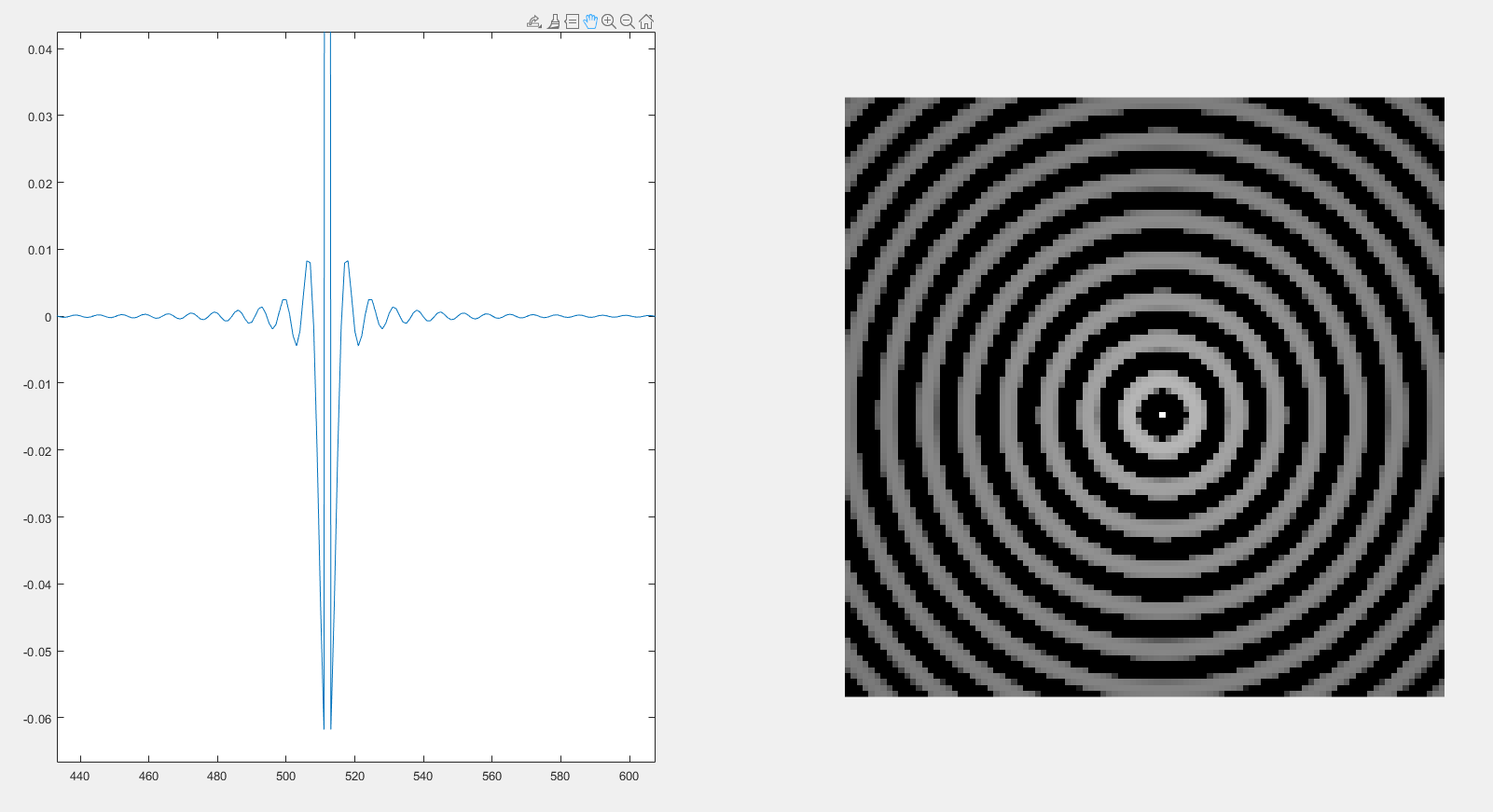
2、巴特沃斯高通滤波器
图像
D0 = 30,m = 1
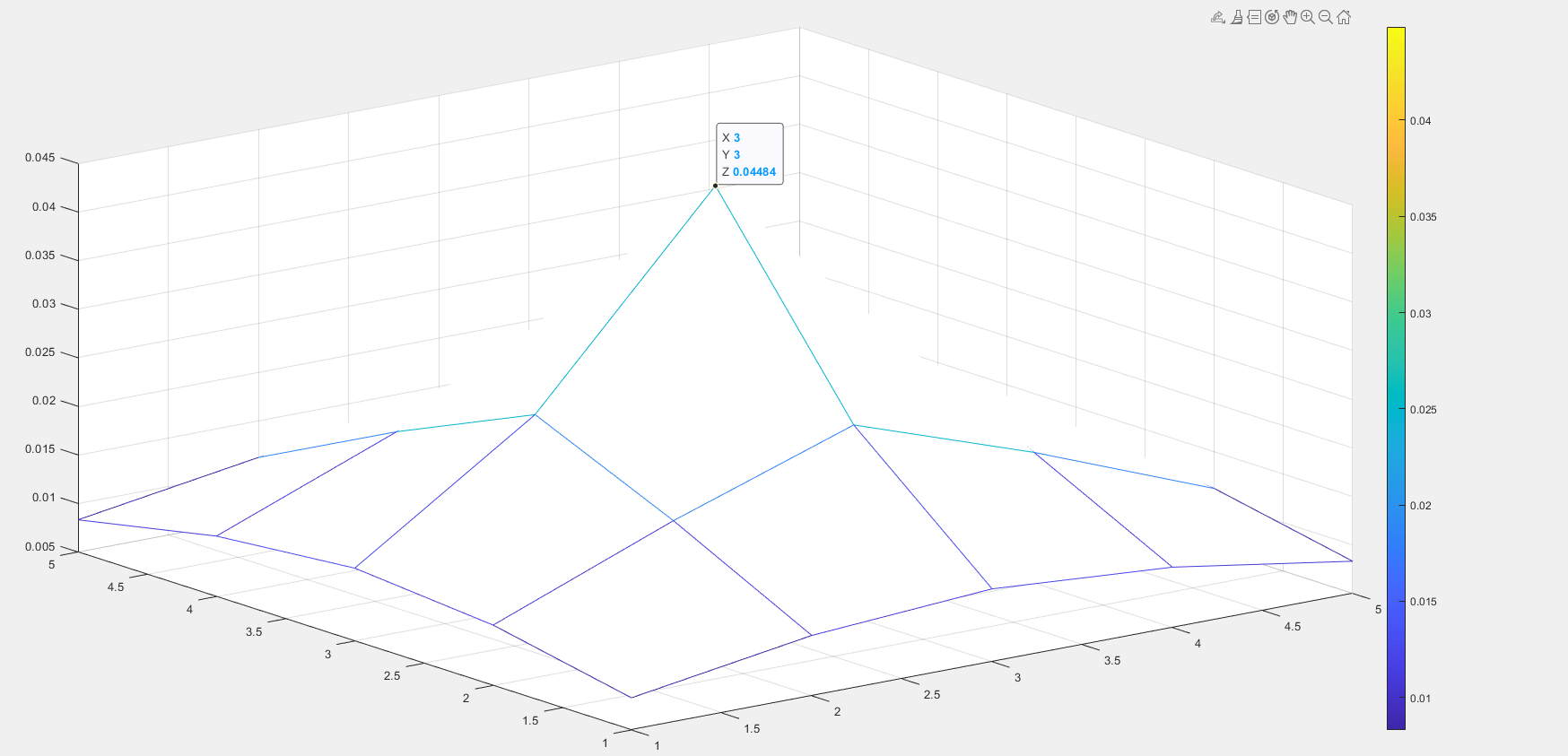
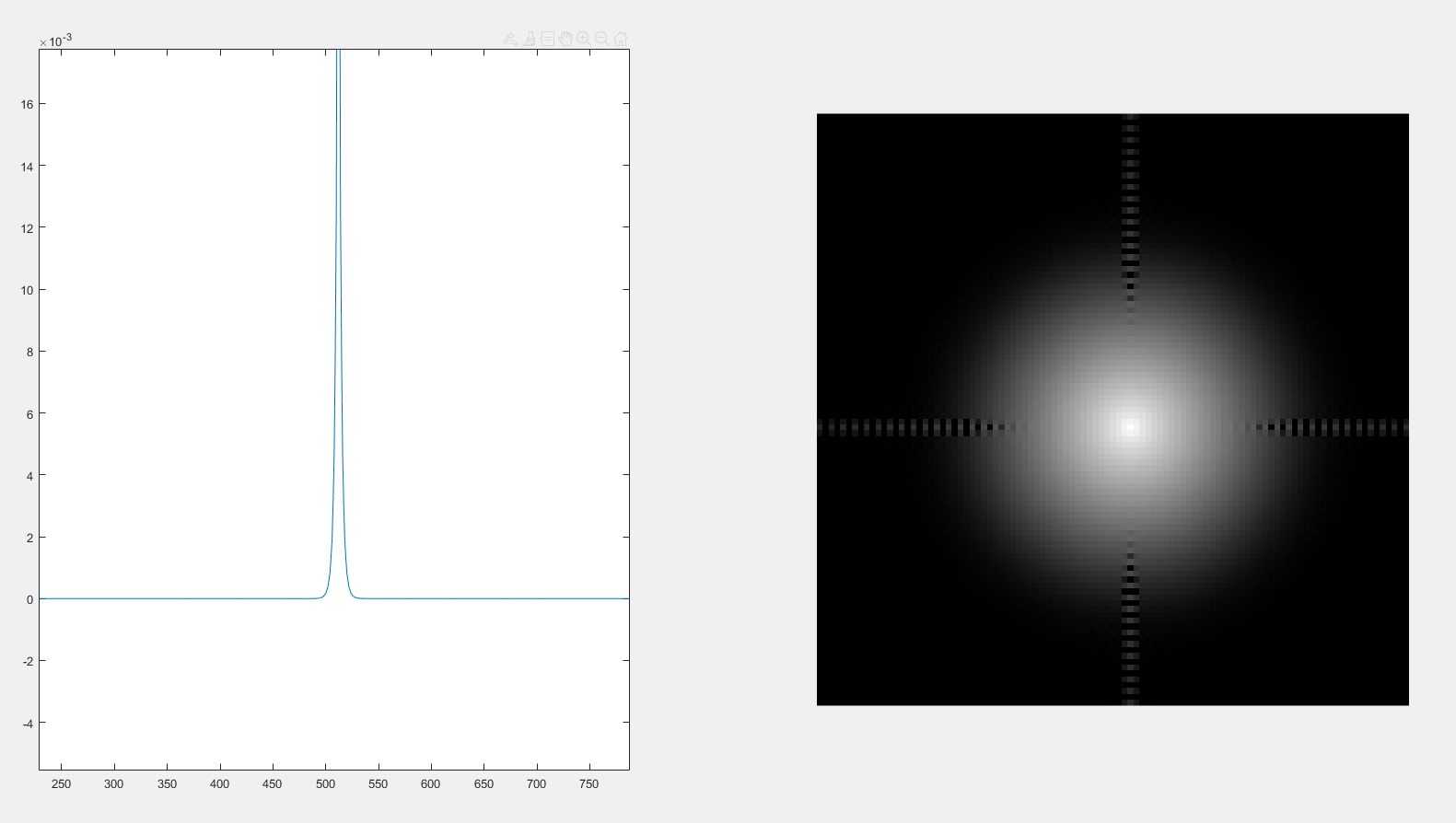
D0 = 80,m = 1
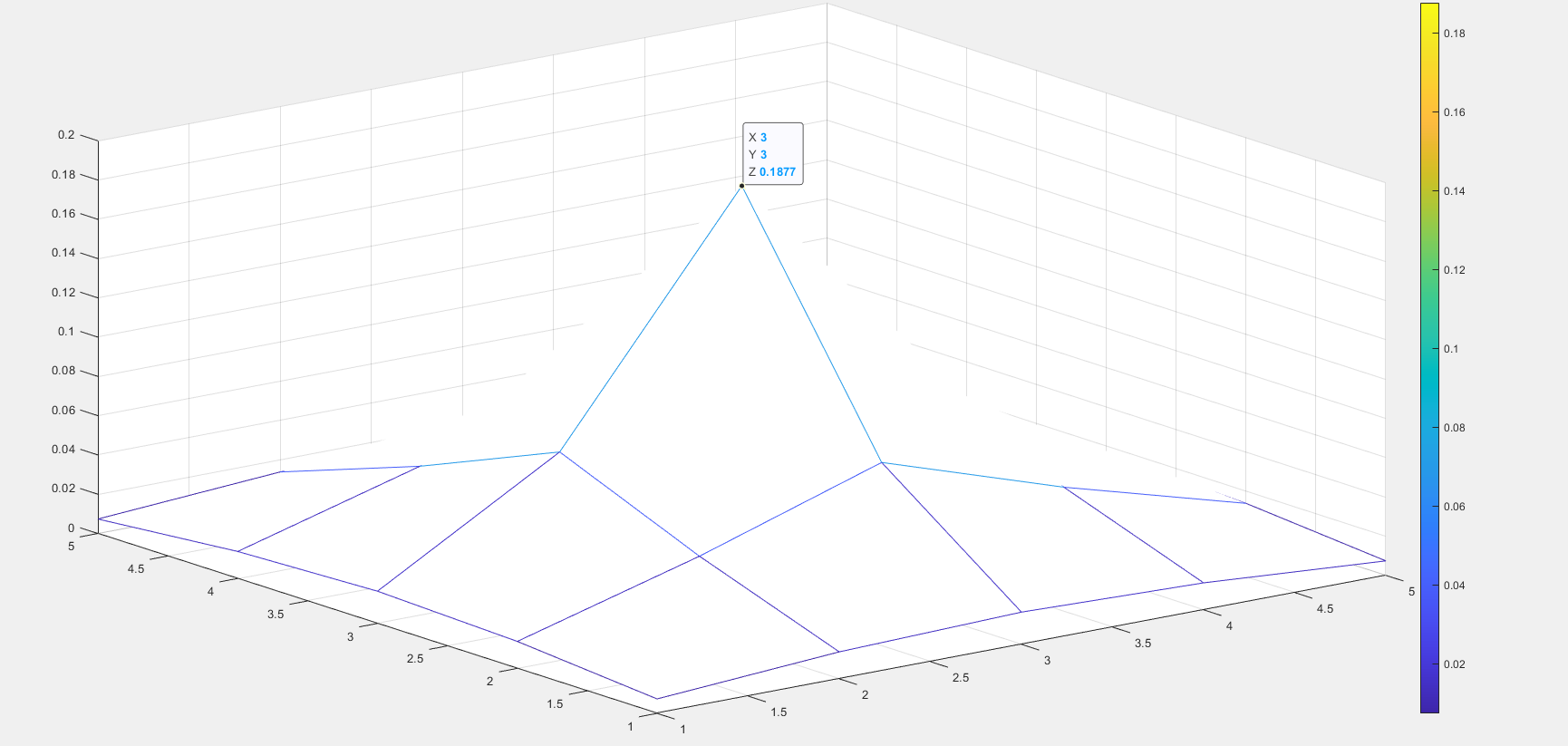
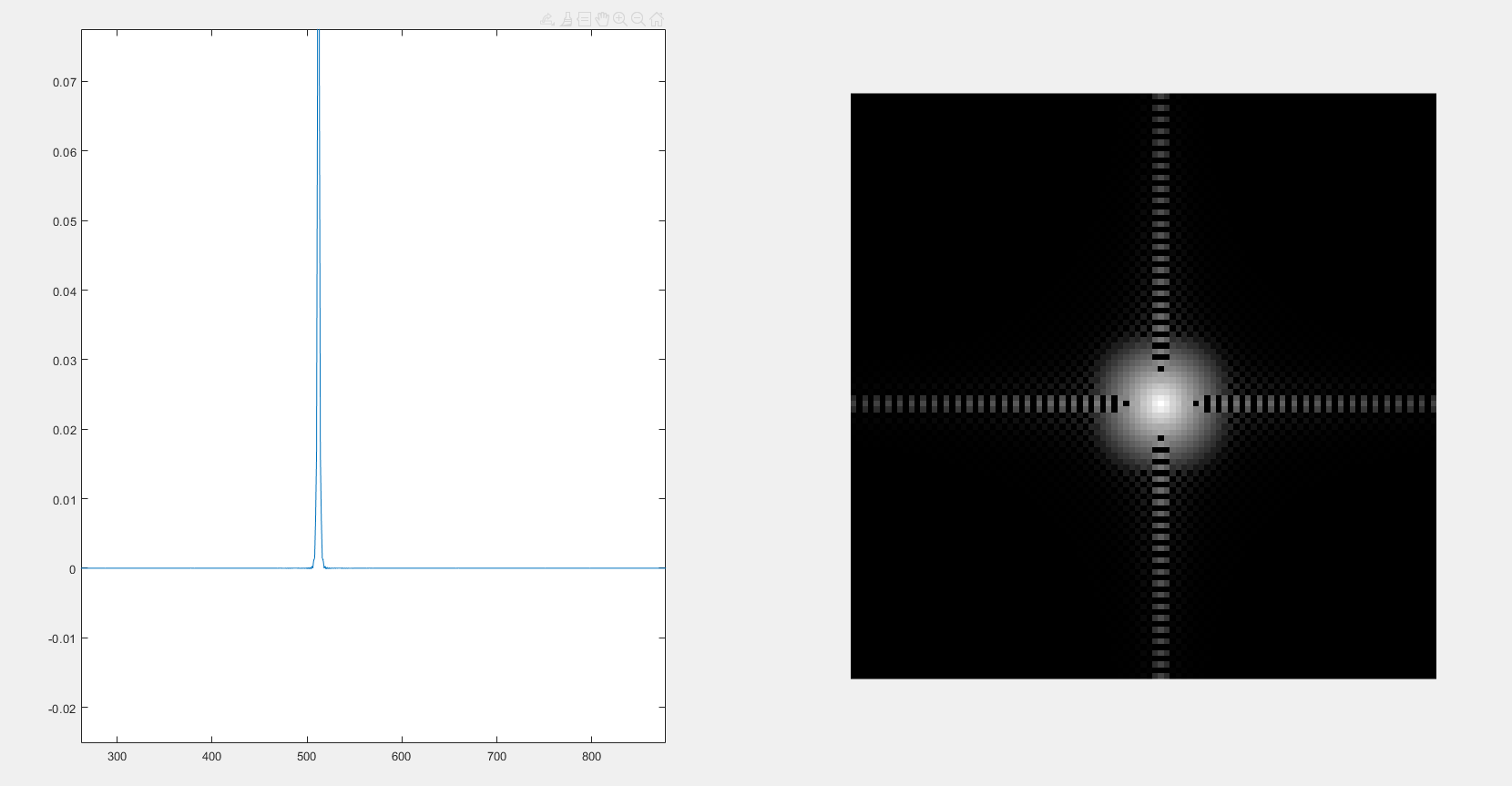
D0 = 30,m = 2
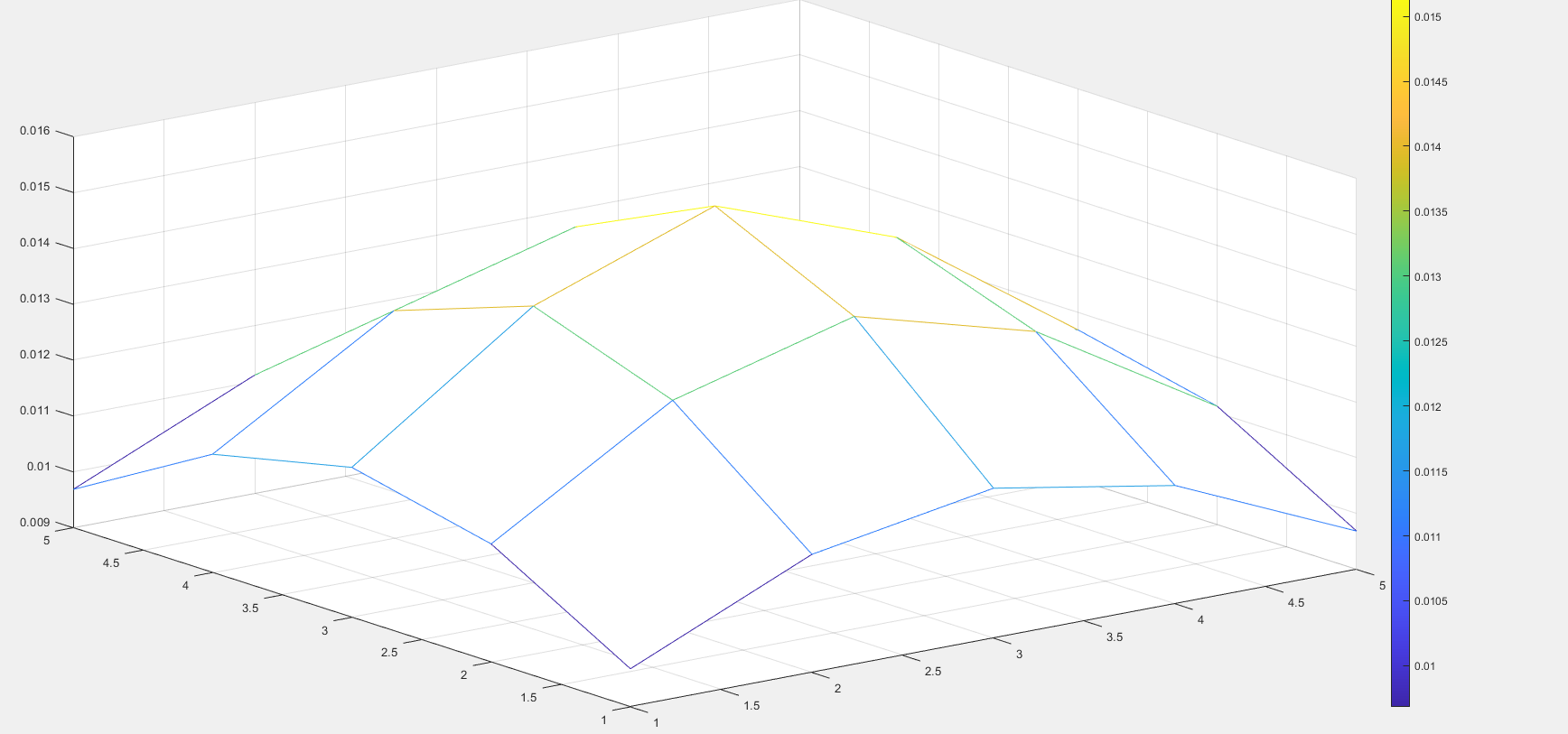
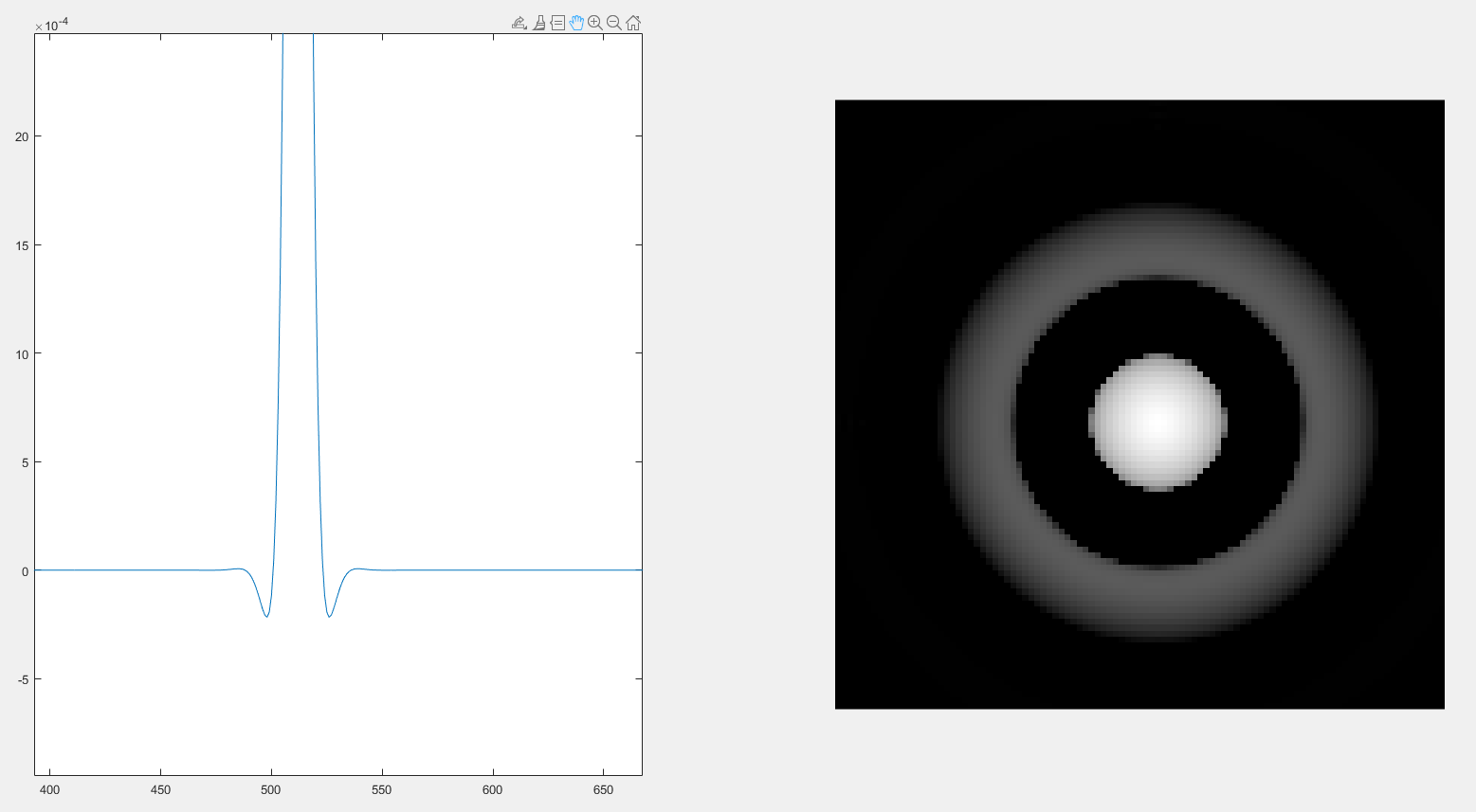
D0 = 30,m = 8
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53clear close all %输入半径参数及滤波器级数 D0 = [30 80]; m = [1 2 8]; Di = 1; Mi = 3; %图像预处理（归一化及填充） aIn = imread('Moon.jpg'); aDouble = double(aIn); a1Double = aDouble/(max(max(aDouble))); [ra,ca] = size(aDouble); maxL = max(ra,ca); n = 1; while(maxL>2^n) n = n+1; end aFill = zeros(2^n,2^n); aFill(1:ra,1:ca) = a1Double; %提取处理后图像大小，进行滤波器的制作 [Ra,Ca] = size(aFill); [X,Y] = meshgrid(0:Ra-1,0:Ca-1); %更改此部分可以更换D0的值 r = D0(Di)*(Ra/ra); %制作巴特沃斯滤波器 Duv = ((X+1)-round(Ra/2)).^2+((Y+1)-round(Ca/2)).^2; H = 1./(1+((Duv.^m(Mi))./r.^(2.*m(Mi)))); Huv = H.*(-1).^(X+Y); %将滤波器从频域变换到空域观察 ifi = real(ifft2(Huv)); ifiXY = ifi.*(-1).^(X+Y); %w控制滤波器中心输出框大小并输出 w = 2; HxyOut = ifiXY(Ra/2+1-w:Ra/2+1+w,Ca/2+1-w:Ca/2+1+w); figure, mesh(HxyOut) colorbar %显示空域中滤波器形状（剖线及二维图） xianshi = ifiXY(460:560,460:560).*10000000; xianshi(xianshi<0) = 0; x = 0:1023; y = ifiXY(513,:); figure, subplot(121),plot(x,y); subplot(122),imshow(log(xianshi+1),[]);
分析
当m = 1（巴特沃斯滤波器的级数）时，绝对不会发生振铃现象。
当m = 1时，随着D0（巴特沃斯滤波器半径）增大时，零频增大，中心点变亮。
当D0 = 30时，随着m（巴特沃斯滤波器级数）增大时，振铃出现（m>=2就会出现振铃），并且随着m的增大，振铃现象越来越明显。
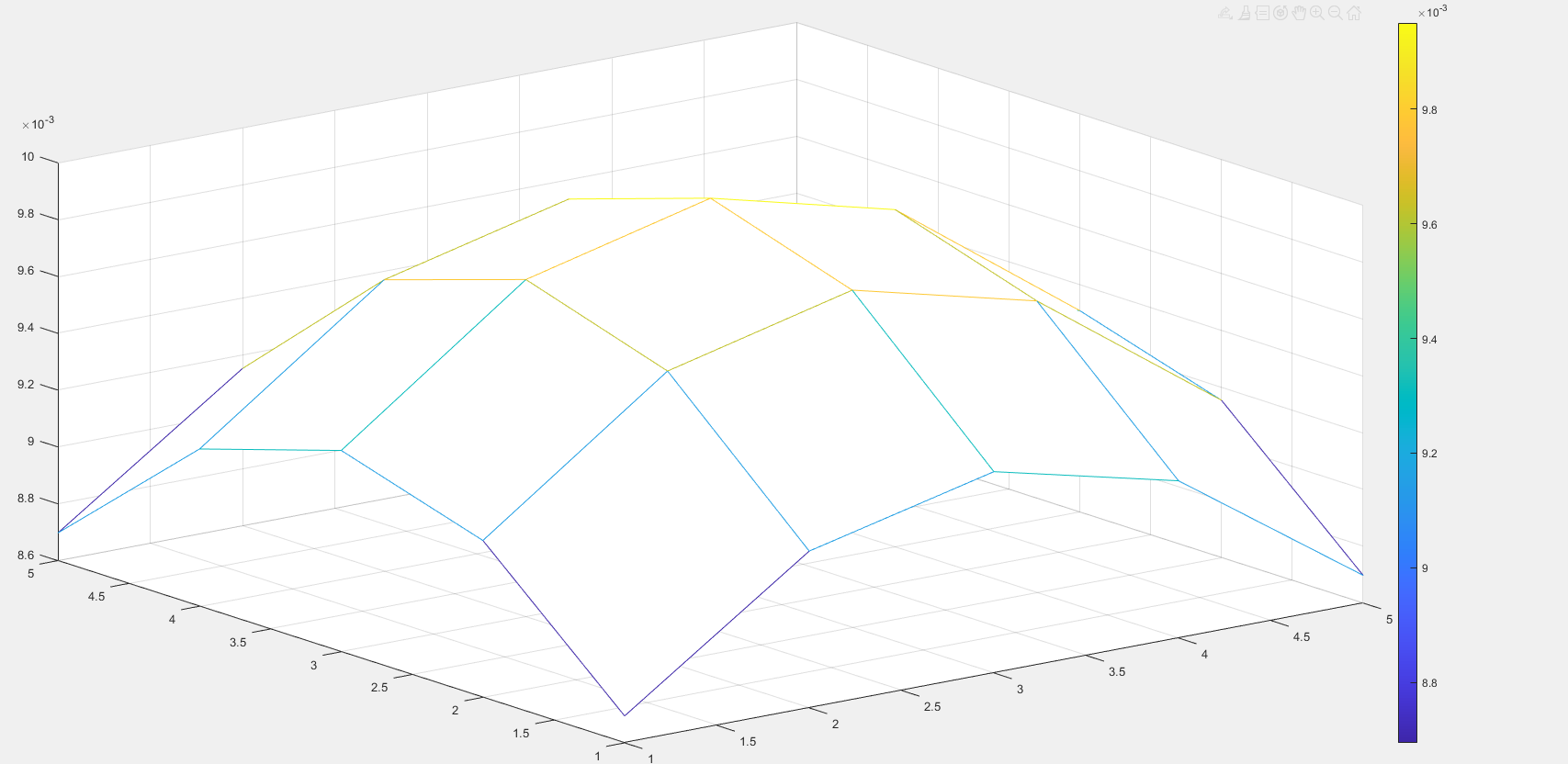
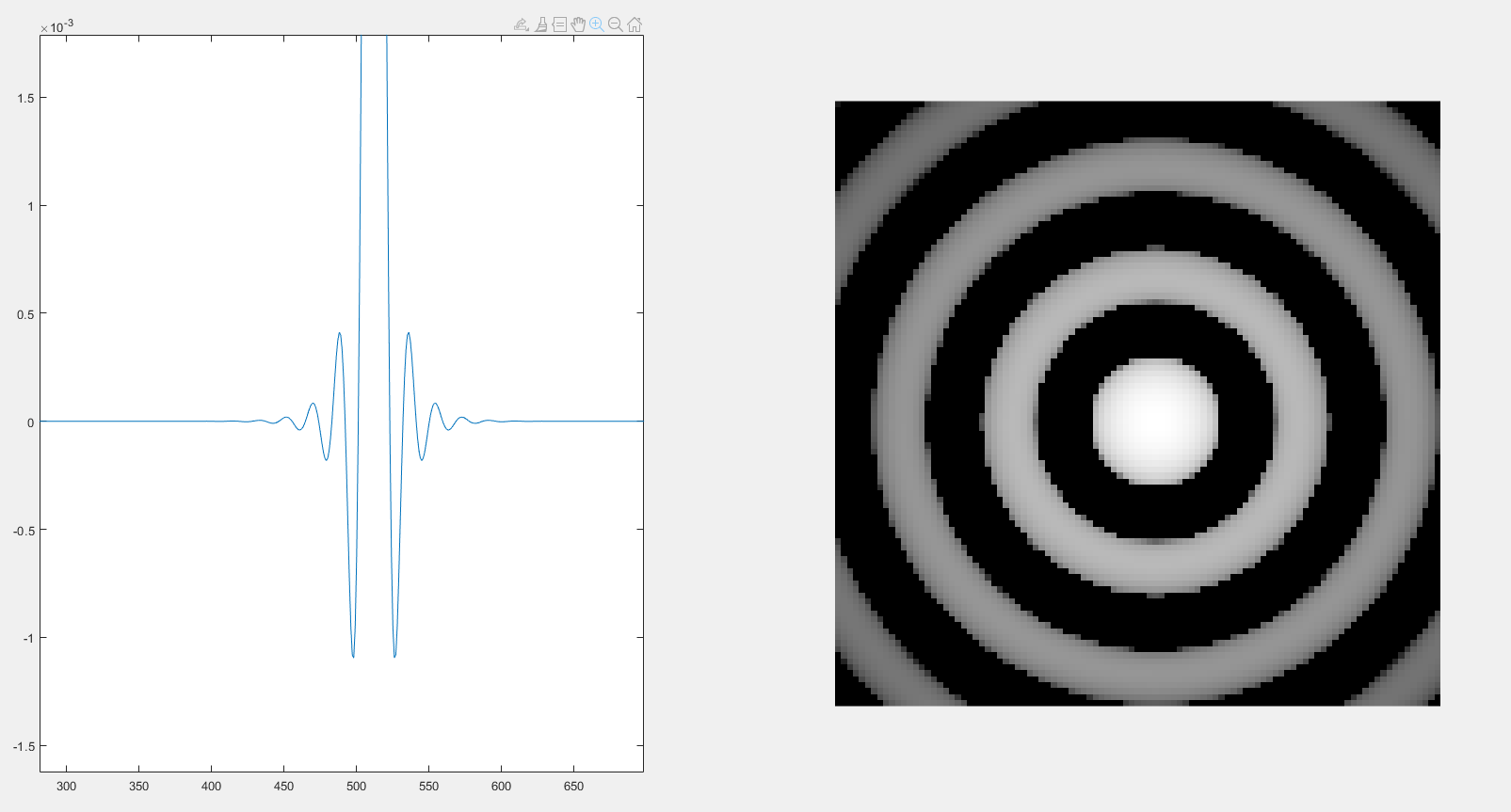
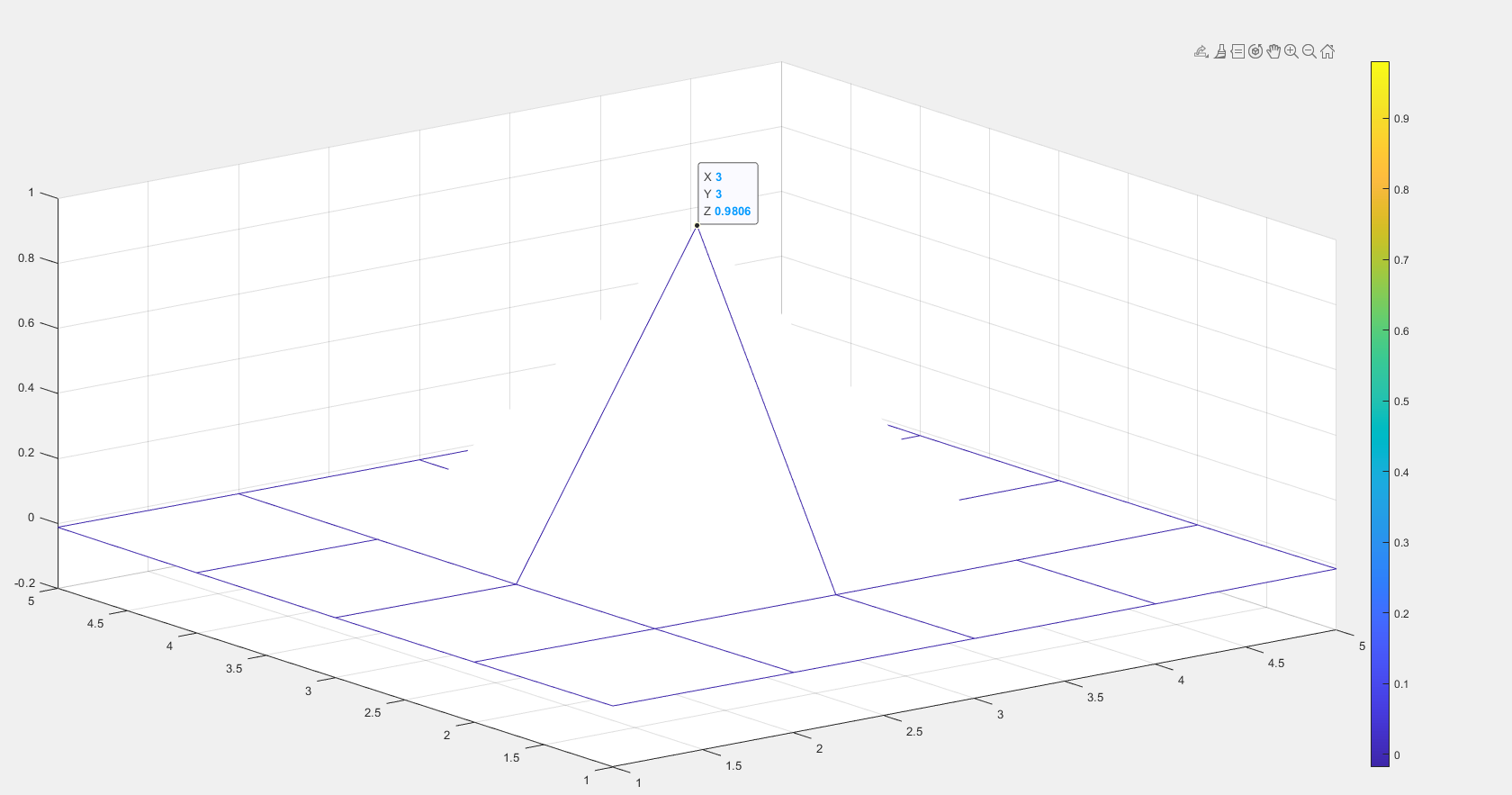
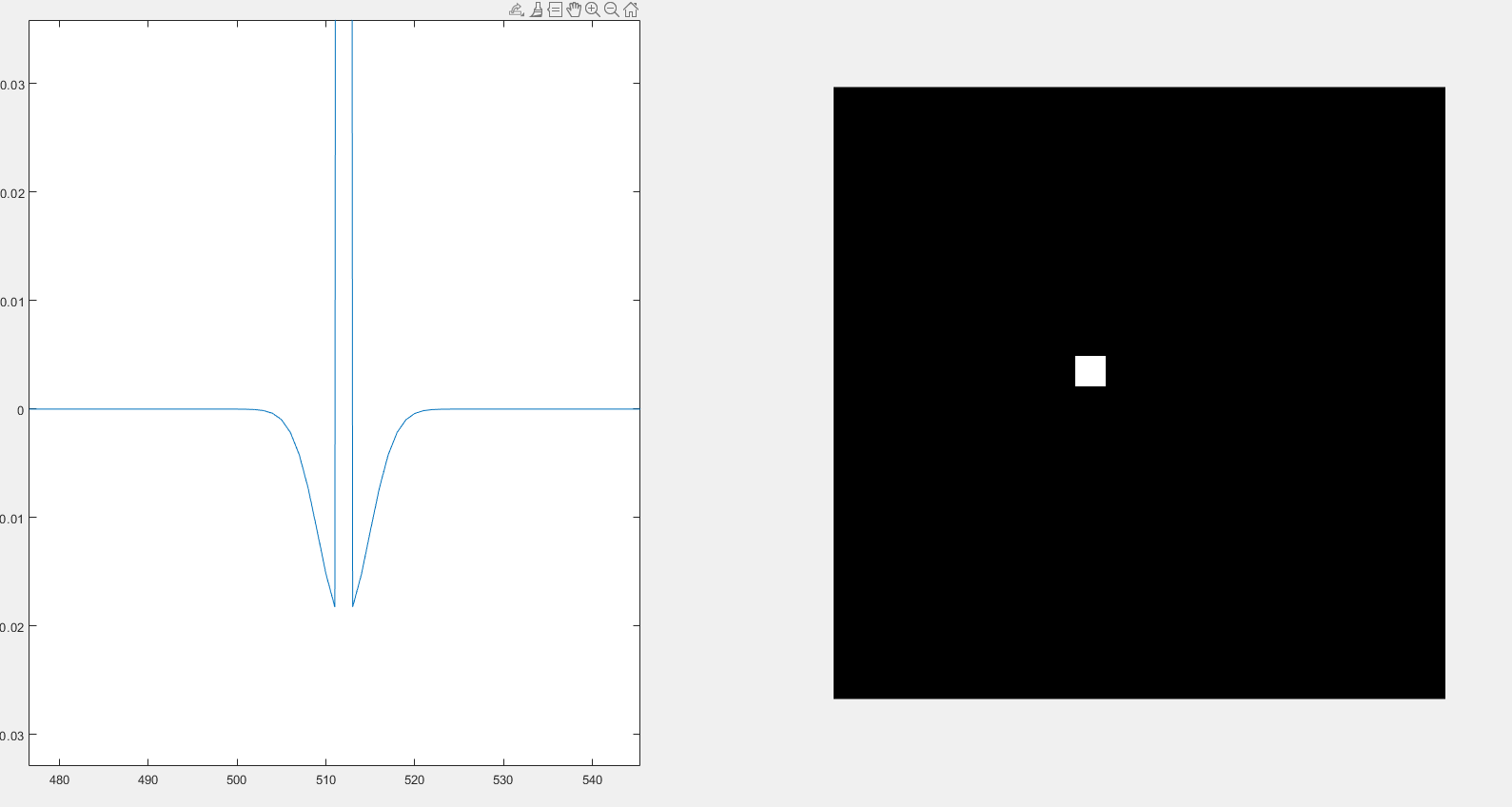
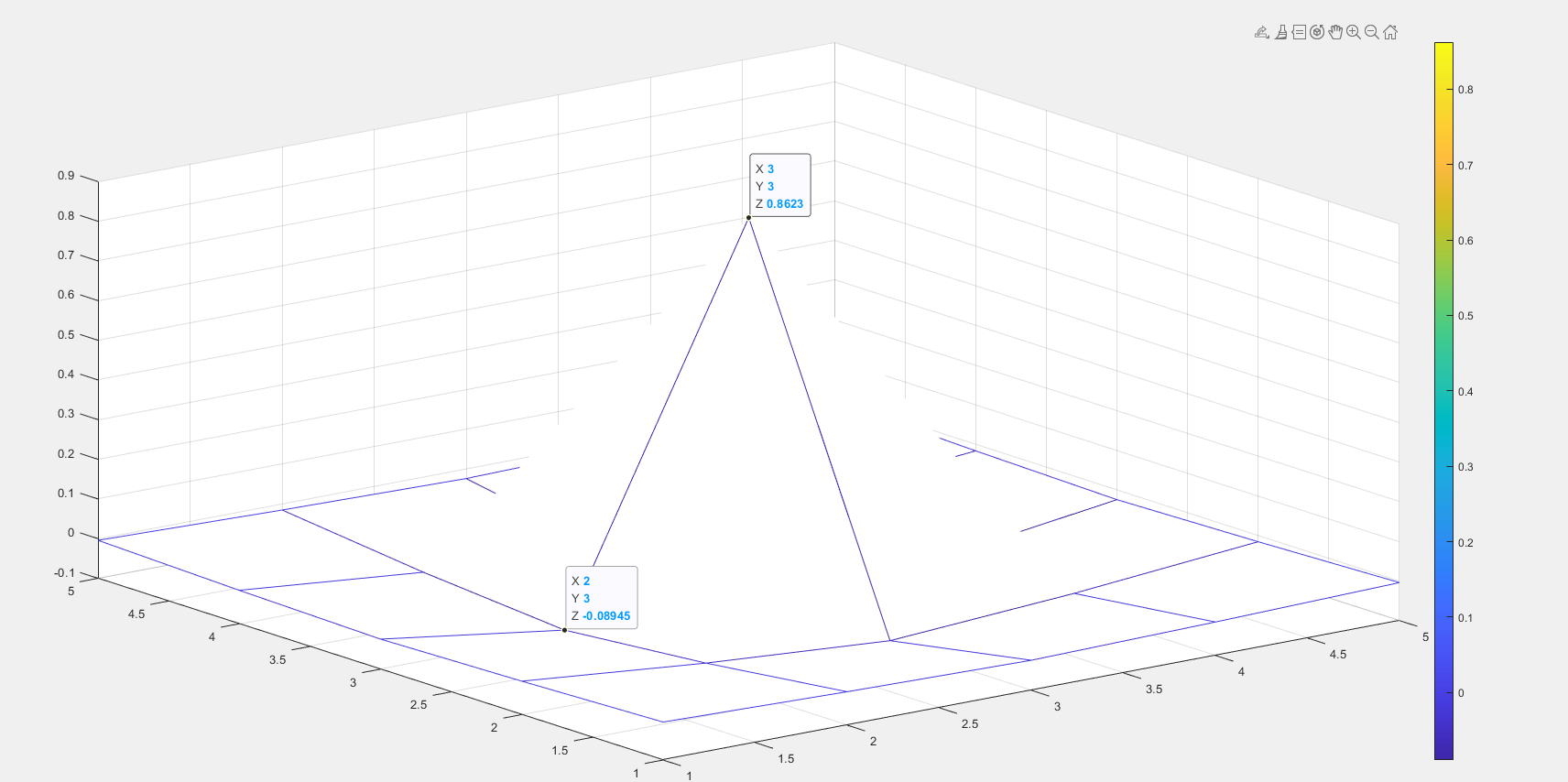
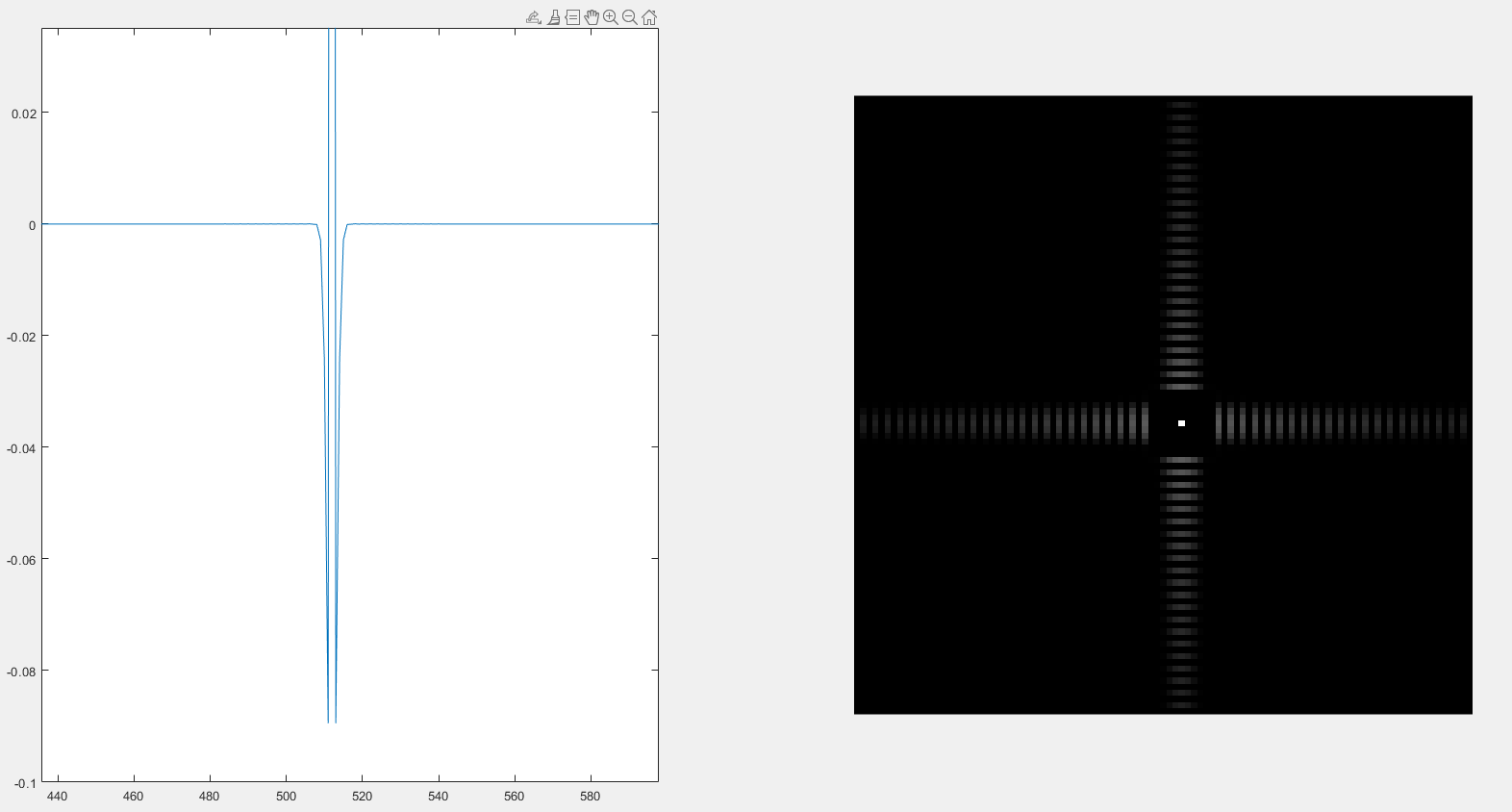
3、高斯高通滤波器
图像
D0 = 30
D0 = 80
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51clear close all %输入半径及滤波器级数 D0 = [30 80]; Di = 2; %图像预处理（归一化及填充） aIn = imread('Moon.jpg'); aDouble = double(aIn); a1Double = aDouble/(max(max(aDouble))); [ra,ca] = size(aDouble); maxL = max(ra,ca); n = 1; while(maxL>2^n) n = n+1; end aFill = zeros(2^n,2^n); aFill(1:ra,1:ca) = a1Double; %提取处理后图像大小，进行滤波器的制作 [Ra,Ca] = size(aFill); [X,Y] = meshgrid(0:Ra-1,0:Ca-1); %更改此部分可以更换D0的值 r = D0(Di)*(Ra/ra); %制作高斯滤波器 Duv = ((X+1)-(Ra/2)).^2+((Y+1)-(Ca/2)).^2; H = 1-exp(-1.*Duv./(2.*r.^2)); Huv = H.*(-1).^(X+Y); %将滤波器从频域变换到空域观察 ifi = real(ifft2(Huv)); ifiXY = ifi.*(-1).^(X+Y); %w控制滤波器中心输出框大小并输出 w = 2; l = ifiXY(Ra/2+1-w:Ra/2+1+w,Ca/2+1-w:Ca/2+1+w); figure,mesh(l) colorbar %显示空域中滤波器形状（剖线及二维图） xianshi = ifiXY(460:560,460:560).*10000000; xianshi(xianshi<0) = 0; x = 0:1023; y = ifiXY(513,:); figure, subplot(121),plot(x,y); subplot(122),imshow(log(xianshi+1),[]);
分析
高斯滤波器绝对不会出现振铃，随着D0（高斯滤波器半径）增大时，中心点变暗。
4、拉普拉斯高通滤波器
图像
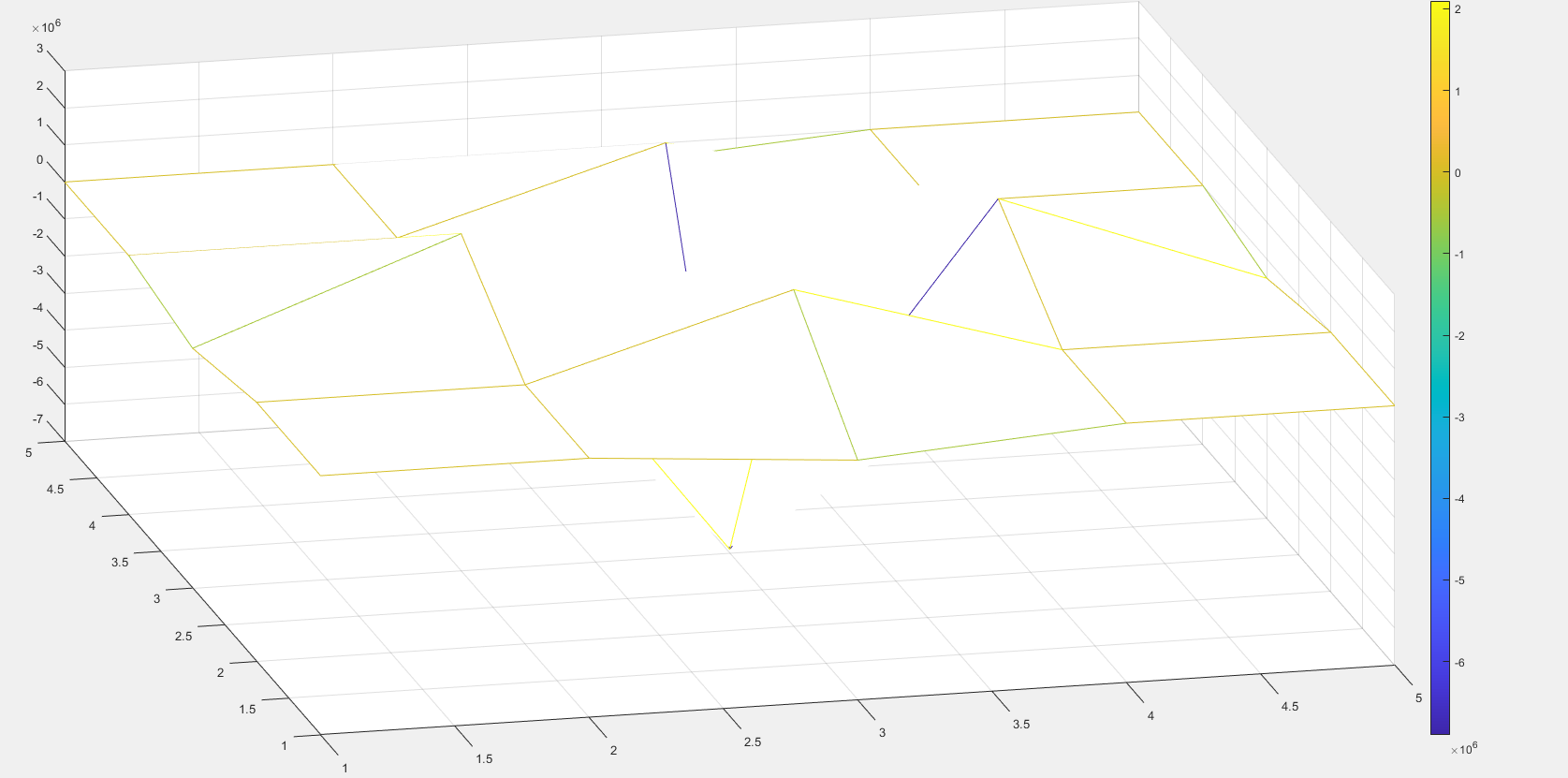
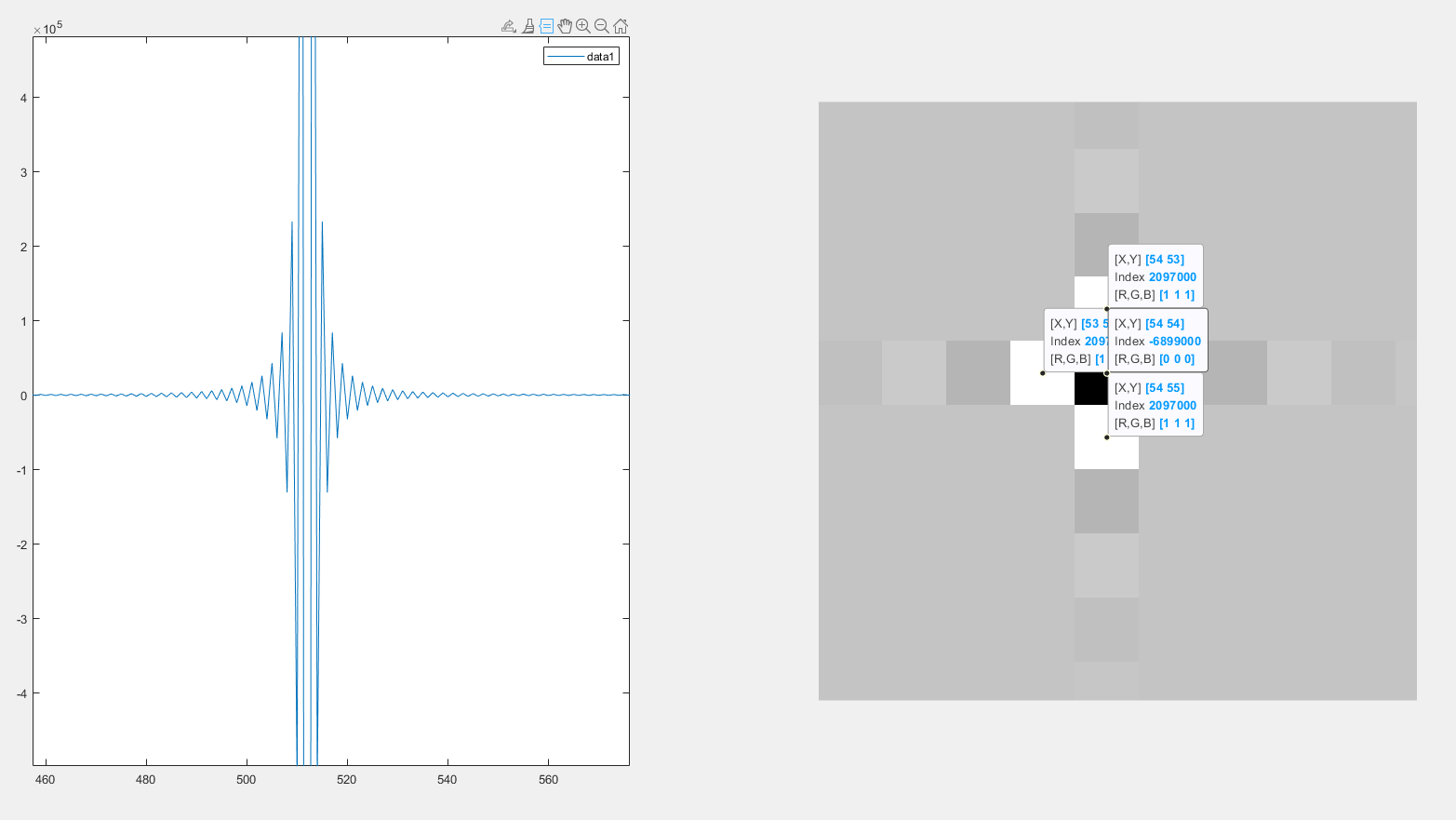
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44clear close all %图像预处理（归一化及填充） aIn = imread('Moon.jpg'); aDouble = double(aIn); a1Double = aDouble/max(max(aDouble)); [ra,ca] = size(a1Double); maxL = max(ra,ca); n = 1; while(maxL>2^n) n = n+1; end aFill = zeros(2^n,2^n); aFill(1:ra,1:ca) = a1Double; %提取处理后图像大小，进行滤波器的制作 [Ra,Ca] = size(aFill); [X,Y] = meshgrid(0:Ra-1,0:Ca-1); %制作滤波器 Duv = ((X+1)-(Ra/2)).^2+((Y+1)-(Ca/2)).^2; H = -4*pi^2.*Duv; Huv = H.*(-1).^(X+Y); %将滤波器从频域变换到空域观察 ifi = ifft2(Huv); ifi1 = real(ifi); ifiXY = ifi1.*(-1).^(X+Y); %w控制滤波器中心输出框大小并输出 w = 2; laplace = ifiXY(Ra/2+1-w:Ra/2+1+w,Ca/2+1-w:Ca/2+1+w); figure,mesh(laplace) colorbar %显示空域中滤波器形状（剖线及二维图） xianshi = ifiXY(460:560,460:560); x = 0:1023; y = ifiXY(513,:); figure, subplot(121),plot(x,y); subplot(122),imshow(xianshi,[]);
分析
);
[ra,ca] = size(a1Double);
maxL = max(ra,ca);
n = 1;
while(maxL>2^n)
n = n+1;
end
aFill = zeros(2n,2n);
aFill(1:ra,1:ca) = a1Double;
%提取处理后图像大小，进行滤波器的制作
[Ra,Ca] = size(aFill);
[X,Y] = meshgrid(0:Ra-1,0:Ca-1);
%制作滤波器
Duv = ((X+1)-(Ra/2)).2+((Y+1)-(Ca/2)).2;
H = -4*pi^2.Duv;
Huv = H.(-1).^(X+Y);
%将滤波器从频域变换到空域观察
ifi = ifft2(Huv);
ifi1 = real(ifi);
ifiXY = ifi1.*(-1).^(X+Y);
%w控制滤波器中心输出框大小并输出
w = 2;
laplace = ifiXY(Ra/2+1-w:Ra/2+1+w,Ca/2+1-w:Ca/2+1+w);
figure,mesh(laplace)
colorbar
%显示空域中滤波器形状（剖线及二维图）
xianshi = ifiXY(460:560,460:560);
x = 0:1023;
y = ifiXY(513,:);
figure,
subplot(121),plot(x,y);
subplot(122),imshow(xianshi,[]);
1
2
3
4
5
6#### 分析 拉普拉斯频域算子在空域中显示后，正中心位置为（负数）-6899000，其直接相邻的四个格子均为（正数）2097000，基于此，其周围点绝对值不断减小，中心点的绝对值最大（符合空域中拉普拉斯算子变化规律）
最后
以上就是美好睫毛最近收集整理的关于matlab 对三种高通滤波器（理想高通 巴特沃斯高通 高斯高通）及拉普拉斯增强算子 自写算法实现及比较 在时域中分析的全部内容，更多相关matlab内容请搜索靠谱客的其他文章。
![[数字图像处理]频域滤波(2)--高通滤波器，带阻滤波器与陷波滤波器](/uploads/reation/bcimg5.png)
发表评论 取消回复