MFCC特征提取过程

接下来详细写下语音提取MFCC特征的过程。提取MFCC的流程（以提取39维MFCC特征为例）如图所示。

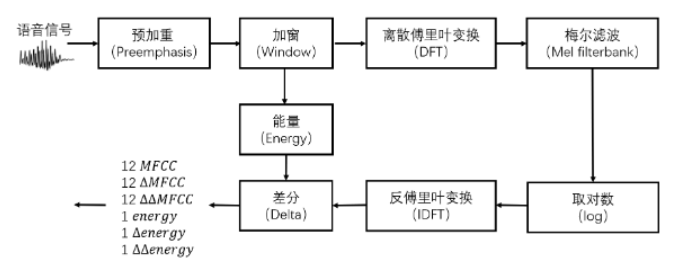
• 预加重：预加重的作用是提升高频。对于语音中发声的部分，比如元音，它的频谱中高频的能量在传播中有比较明显的衰减，因此采用预加重的方法对高频部分进行补偿。对于n时刻语音的采样值????[????]，经过预加重处理后得到的输出：
  $$y[n]=x[n]-a\ast x[n-1]$$
  预加重系数????的取值一般在0.9到1之间。预加重相当于将信号通过一个高通滤波器，能够提升高频的能量，帮助提升识别的效果。
• 加窗：语音信号在时间上是不断变化的，是不平稳的信号。但是在比较短的时间段内，可以近似认为它是平稳的，可以通过短时的表现和它的分布特征判断出该短时语音属于某个音素(phone)或子音素(sub-phone)。通过加窗操作将语音分割成一个个小段，窗函数只在一些区域非零，而在其他区域都为零。常见的窗函数有矩形窗、汉明窗、汉宁窗等。假设窗的长度包括L个采样点。矩形窗的公式为：
  $$w_r[n]=\{\begin{array}{ll}1& 0\le n\le L-1\\ 0& \text{ otherwise }\end{array}$$
  汉明窗的公式为：
  $$w[n]=\{\begin{array}{ll}0.54-0.46\cos \left(\frac{2\pi n}{L}\right)& 0\le n\le L-1\\ 0& \text{ otherwise }\end{array}$$
  假设n时刻，信号的值为????[????]，窗函数的值为????[????]，加窗之后得到：
  $$y[n]=x[n]\ast w[n]$$
  窗函数非零区域所覆盖的时长称为帧长(frame size)，两个连续的窗之间平移的时长称为帧移(frame shift)。在语音识别中常用的帧长帧移分别是25ms、10ms。帧长和帧移的概念可以形象地表示如图。
  
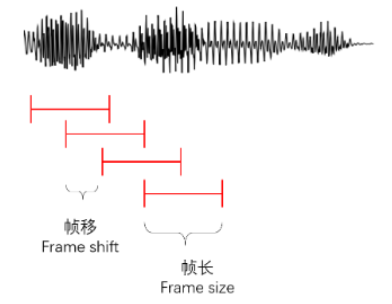
  窗函数一般不选矩形窗而选择汉明窗，因为矩形窗在时域的迅速截断造成了频域的频谱泄露，与原信号频谱相乘时会造成原信号失真，因此常常选用截断比较平缓的汉明窗。
• 离散傅里叶变换：加窗分帧的下一步是离散傅里叶变换(DFT, Discrete FourierTransform)。傅里叶变换的作用是将信号从时域映射到频域。假设加窗后的采样点个数是N，那么对这N个点做DFT有：
  $$X[k]=\sum _{n=0}^{N-1}x[n]e^{-j2\frac{\pi }{N}kn}$$
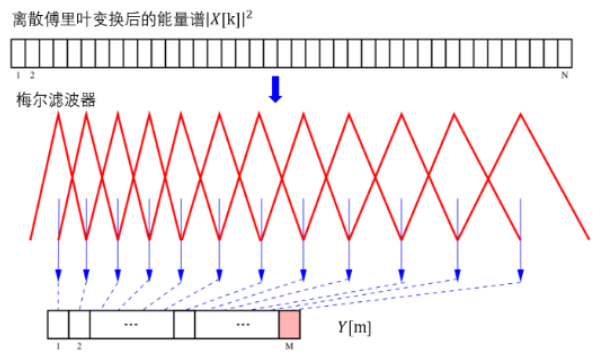
  由于傅里叶变换的因子具有对称性，利用傅里叶变换的因子的对称性可以快速计算离散时间傅里叶变换。快速计算DFT的算法被称为快速傅里叶变换（FFT, FastFourier Transform）。只有在采样点个数为2的指数时，才能应用快速傅里叶变换对DFT加速。一般当采样点不是2的指数时，补零成2的指数个点，再应用快速傅里叶变换计算。
• 梅尔滤波：FFT后得到了各个频率分量的幅度，将幅度平方就得到了各个频率分量的能量。人耳对不同频率的敏感程度不同，对低频比较敏感，对高频（高于1000赫兹）相对不敏感。为了模拟人耳的这种特性，将频率映射到梅尔频率，梅尔频率与频率之间的表示关系为：
  $$mel(f)=1127\ast ln(1+\frac{f}{700})$$
  在频率小于1000赫兹时，近似于线性映射，当频率大于1000赫兹时，近似于对数映射。将频率映射到梅尔频率后，接入梅尔滤波器，每个滤波器输出该频带的能量。根据各个梅尔频带中的能量，得到一定维数的特征。特征的维数取决于梅尔滤波器组的滤波器的个数M。
  
• 取对数：对上一步的梅尔特征???? [????]取对数。????????????(???? [????])可以作为声学特征使用，即在神经网络的训练中应用的很广泛的Fbank特征。
• IDFT：这一步也被称为倒谱分析。倒谱的定义是频谱的对数的频谱。即将取了对数的频谱看成是一个时域信号，再做一次傅里叶变换。由于我们声音的内容往往是由声音从发声位置出来经过的路径（类似于经过一系列的滤波器）决定，而与发声位置本身振动的频率（基频）无关。倒谱的作用就是把滤波器和声源分离开，帮助识别声音的内容。倒谱的计算过程如下公式所示，这里面仅表示了倒谱的计算过程，不包括经过梅尔滤波的过程。从倒谱的公式2.1我们可以看出，倒谱就是把经过一次傅里叶变换的频谱，当作时域信号，并在这个频谱上再做一次傅里叶变换。
• $$c[n]=\sum _{n=0}^{N-1}\log \left(\left|\sum _{n=0}^{N-1}x[n]e^{-j\frac{2\pi }{N}kn}\right|\right)e^{j\frac{2\pi }{N}kn}$$label{eq:cel}
• 差分和能量：对于每帧选取经过IDFT的前12维倒谱系数，接着将能量作为第13维特征。加窗后的时域信号通过计算可以得到能量特征，假设窗的长度从????1开始，到????2终止，那么该帧的能量为：
  $$\text{Energy}=\sum _{t=t_1}^{t_2}{x}^2[t]$$
  特征能够表征一定的声学特性，那么特征在时间上的变化也能表征声学特性。在原始的13维特征上加入特征在时间上的变化，即计算delta和double delta。delta特征表示了帧与帧之间倒谱系数和能量的变化，double delta表示了帧与帧之间delta特征的变化。原始的倒谱系数和能量的MFCC特征表示为????[????]，delta特征和double delta特征可以表示为：
  $$delta[n]=\frac{c[n+1]-c[n-1]}{2}$$
  $$doubledelta[n]=\frac{delta[n+1]-delta[n-1]}{2}$$
  最后得到的39维MFCC特征的组成如图所示。
  

最后

以上就是怡然鸡为你收集整理的MFCC特征提取过程的全部内容，希望文章能够帮你解决MFCC特征提取过程所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。