离散傅里叶与卷积
离散傅里叶变换公式:
X
(
k
)
=
∑
n
=
0
N
−
1
x
n
e
−
j
2
π
k
n
N
X(k)=sum_{n=0}^{N-1}x_ne^{-jfrac{2pi kn}{N}}
X(k)=n=0∑N−1xne−jN2πkn
下文中将
e
−
j
2
π
k
n
N
e^{-jfrac{2pi kn}{N}}
e−jN2πkn 记为
W
N
k
n
W_N^{kn}
WNkn 也就是DFT变换公式下文记为
X
(
k
)
=
∑
n
=
0
N
−
1
x
n
W
N
k
n
X(k)=sum_{n=0}^{N-1}x_nW^{kn}_{N}
X(k)=n=0∑N−1xnWNkn
那么离散傅里叶逆变换IDFT表示为:
X
n
=
∑
k
=
0
N
−
1
X
(
k
)
W
N
−
k
n
Xn=sum_{k=0}^{N-1}X(k)W^{-kn}_{N}
Xn=k=0∑N−1X(k)WN−kn
离散数字的卷积公式:
x
n
=
∑
m
=
0
M
−
1
u
(
n
−
m
)
v
(
m
)
,
v
为
M
个
数
据
序
列
(
卷
积
核
)
,
u
为
N
个
数
据
序
列
当
n
−
m
小
于
零
时
,
u
补
零
(
等
于
零
)
x_n=sum_{m=0}^{M-1} u(n-m)v(m) ,v为M个数据序列(卷积核),u为N个数据序列 \ 当n-m小于零时,u补零(等于零)
xn=m=0∑M−1u(n−m)v(m) ,v为M个数据序列(卷积核),u为N个数据序列当n−m小于零时,u补零(等于零)
离散数字的卷积与傅里叶变换的关系:
卷积后的DFT为:
X
(
k
)
=
∑
n
=
0
N
−
1
x
n
W
N
k
n
=
∑
n
=
0
N
−
1
W
N
k
n
(
∑
m
=
0
M
−
1
u
(
n
−
m
)
v
(
m
)
)
=
∑
n
=
0
N
−
1
(
∑
m
=
0
M
−
1
u
(
n
−
m
)
v
(
m
)
W
N
k
n
)
begin{aligned} X(k) &= sum_{n=0}^{N-1}x_nW^{kn}_{N} hspace{8cm} \ &= sum_{n=0}^{N-1}W^{kn}_{N}left( sum_{m=0}^{M-1} u(n-m)v(m) right) \ &= sum_{n=0}^{N-1}left( sum_{m=0}^{M-1} u(n-m)v(m)W^{kn}_{N} right) \ end{aligned}
X(k)=n=0∑N−1xnWNkn=n=0∑N−1WNkn(m=0∑M−1u(n−m)v(m))=n=0∑N−1(m=0∑M−1u(n−m)v(m)WNkn)
上面最后化简公式从m维度先求和 跟从n维度先求和 结果是一样的 也就是说
∑
n
=
0
N
−
1
(
∑
m
=
0
M
−
1
u
(
n
−
m
)
v
(
m
)
W
N
k
n
)
=
∑
m
=
0
M
−
1
(
∑
n
=
0
N
−
1
u
(
n
−
m
)
v
(
m
)
W
N
k
n
)
begin{aligned} sum_{n=0}^{N-1}left( sum_{m=0}^{M-1} u(n-m)v(m)W^{kn}_{N} right) hspace{4cm} \ =sum_{m=0}^{M-1}left( sum_{n=0}^{N-1} u(n-m)v(m)W^{kn}_{N} right) hspace{4cm} end{aligned}
n=0∑N−1(m=0∑M−1u(n−m)v(m)WNkn)=m=0∑M−1(n=0∑N−1u(n−m)v(m)WNkn)
继续化简
所以有卷积后的DFT为:
X
(
k
)
=
∑
m
=
0
M
−
1
(
∑
n
=
0
N
−
1
u
(
n
−
m
)
v
(
m
)
W
N
k
n
)
=
∑
m
=
0
M
−
1
(
∑
n
=
0
N
−
1
u
(
n
−
m
)
v
(
m
)
W
N
k
n
)
=
∑
m
=
0
M
−
1
(
∑
n
=
0
N
−
1
u
(
n
−
m
)
v
(
m
)
W
N
k
(
n
−
m
)
W
N
k
m
)
=
∑
m
=
0
M
−
1
v
(
m
)
W
N
k
m
(
∑
n
=
0
N
−
1
u
(
n
−
m
)
W
N
k
(
n
−
m
)
)
begin{aligned} X(k) &= sum_{m=0}^{M-1}left( sum_{n=0}^{N-1} u(n-m)v(m)W^{kn}_{N} right) hspace{4cm} \ &= sum_{m=0}^{M-1}left( sum_{n=0}^{N-1} u(n-m)v(m)W^{kn}_{N} right) \ &= sum_{m=0}^{M-1}left( sum_{n=0}^{N-1} u(n-m)v(m)W^{k(n-m)}_{N}W^{km}_{N} right) \ &= sum_{m=0}^{M-1}v(m)W^{km}_{N}left( sum_{n=0}^{N-1} u(n-m)W^{k(n-m)}_{N} right) end{aligned}
X(k)=m=0∑M−1(n=0∑N−1u(n−m)v(m)WNkn)=m=0∑M−1(n=0∑N−1u(n−m)v(m)WNkn)=m=0∑M−1(n=0∑N−1u(n−m)v(m)WNk(n−m)WNkm)=m=0∑M−1v(m)WNkm(n=0∑N−1u(n−m)WNk(n−m))
化简结果跟
X
(
k
)
=
∑
n
=
0
N
−
1
x
n
W
N
k
n
X(k)=sum_{n=0}^{N-1}x_nW^{kn}_{N}
X(k)=∑n=0N−1xnWNkn 是有相似的形式的,
如果化简的后半部分是
∑
n
−
m
=
0
N
−
1
u
(
n
−
m
)
W
N
k
(
n
−
m
)
sum_{n-m=0}^{N-1} u(n-m)W^{k(n-m)}_{N}
∑n−m=0N−1u(n−m)WNk(n−m),就可以认为离散数据卷积后
的DFT等于卷积前两函数的DFT相乘了,但是实际上不是啊
那么,
∑
n
=
0
N
−
1
u
(
n
−
m
)
W
N
k
(
n
−
m
)
sum_{n=0}^{N-1} u(n-m)W^{k(n-m)}_{N}
∑n=0N−1u(n−m)WNk(n−m) 和
∑
n
−
m
=
0
N
−
1
u
(
n
−
m
)
W
N
k
(
n
−
m
)
sum_{n-m=0}^{N-1} u(n-m)W^{k(n-m)}_{N}
∑n−m=0N−1u(n−m)WNk(n−m) 有没有什么关系呢?
当m=0时,它们是相等的,
当m>0 ,n-m<0时 u(n-m)恒等于0 ,且令 n>N-1 u(n-m)也等于0
有n-m<0 和 n>N-1 时
W
N
k
(
n
−
m
)
×
0
=
0
W_{N}^{k(n-m)}times 0=0
WNk(n−m)×0=0
则下面的等式是成立的
∑
n
=
0
N
−
1
u
(
n
−
m
)
W
N
k
(
n
−
m
)
=
∑
n
=
m
m
+
N
−
1
u
(
n
−
m
)
W
N
k
(
n
−
m
)
=
U
′
(
k
)
begin{aligned} sum_{n=0}^{N-1} u(n-m)W^{k(n-m)}_{N} &= sum_{n=m}^{m+N-1} u(n-m)W^{k(n-m)}_{N} \ &=U'(k) end{aligned}
n=0∑N−1u(n−m)WNk(n−m)=n=m∑m+N−1u(n−m)WNk(n−m)=U′(k)
U
′
(
k
)
U'(k)
U′(k)是从原来u数据序列抽取第0,1,2…N-1-m; N-m个数,再补m个零组成一个新的N个数据u’的DFT结果,
显然U’(k)与原来u数据序列DFT结果U(k)是不相等的,但当N远远大于m时,U’(k)与U(k)是差不多相等的;因为从一组N个数据中抽取大部分数,补零后重新组成新的N个数据,两者的频普是差不多相等的
,也可以说DFT是差不多相等的
所以对上面的公式进一步化简
X
(
k
)
=
∑
m
=
0
M
−
1
v
(
m
)
W
N
k
m
(
∑
n
=
0
N
−
1
u
(
n
−
m
)
W
N
k
(
n
−
m
)
)
=
∑
m
=
0
M
−
1
v
(
m
)
W
N
k
m
(
∑
n
=
m
m
+
N
−
1
u
(
n
−
m
)
W
N
k
(
n
−
m
)
)
≈
∑
m
=
0
M
−
1
v
(
m
)
W
N
k
m
U
(
k
)
≈
U
(
k
)
∑
m
=
0
M
−
1
v
(
m
)
W
N
k
m
≈
U
(
k
)
V
(
k
)
begin{aligned} X(k) &= sum_{m=0}^{M-1}v(m)W^{km}_{N}left( sum_{n=0}^{N-1} u(n-m)W^{k(n-m)}_{N} right) \ &= sum_{m=0}^{M-1}v(m)W^{km}_{N}left( sum_{n=m}^{m+N-1} u(n-m)W^{k(n-m)}_{N} right) \ & approx sum_{m=0}^{M-1}v(m)W^{km}_{N}U(k) \ & approx U(k)sum_{m=0}^{M-1}v(m)W^{km}_{N} \ & approx U(k)V(k) end{aligned}
X(k)=m=0∑M−1v(m)WNkm(n=0∑N−1u(n−m)WNk(n−m))=m=0∑M−1v(m)WNkm(n=m∑m+N−1u(n−m)WNk(n−m))≈m=0∑M−1v(m)WNkmU(k)≈U(k)m=0∑M−1v(m)WNkm≈U(k)V(k)
这里还有一个问题,就是v没有与u相当的频率数量,要让上面的约等式成立,
也必须补零扩展v
v补零不会对上面说到的N远远大于m条件冲突,因为当m>M-1时,v(m)为零,相当于
∑
m
=
0
M
−
1
v
(
m
)
W
N
k
m
U
(
k
)
sum_{m=0}^{M-1}v(m)W^{km}_{N}U(k)
∑m=0M−1v(m)WNkmU(k)多加了若干个零。(但是v补零会使V(k)引入一些无关的频率,从而使结果误差变大)
X
(
k
)
≈
∑
m
=
0
M
−
1
v
(
m
)
W
N
k
m
U
(
k
)
≈
∑
m
=
0
N
−
1
v
(
m
)
W
N
k
m
U
(
k
)
≈
U
(
k
)
∑
m
=
0
N
−
1
v
(
m
)
W
N
k
m
≈
U
(
k
)
V
(
k
)
begin{aligned} X(k) & approx sum_{m=0}^{M-1}v(m)W^{km}_{N}U(k) \ & approx sum_{m=0}^{N-1}v(m)W^{km}_{N}U(k) \ & approx U(k)sum_{m=0}^{N-1}v(m)W^{km}_{N} \ & approx U(k)V(k) end{aligned}
X(k)≈m=0∑M−1v(m)WNkmU(k)≈m=0∑N−1v(m)WNkmU(k)≈U(k)m=0∑N−1v(m)WNkm≈U(k)V(k)
结论:对离散数据卷积,相当于其频域与卷积核的域相乘,也就是起到滤波的效果
离散数字的乘积与傅里叶变换后卷积的关系:
对两组数据 u,v DFT后的U(k) V(k)进行卷积,再进行傅里叶逆变换:
x
n
=
∑
k
=
0
N
−
1
W
N
−
k
n
(
∑
m
=
0
M
−
1
U
(
k
−
m
)
V
(
m
)
)
=
∑
m
=
0
M
−
1
V
(
m
)
W
N
−
n
m
(
∑
k
=
0
N
−
1
U
(
k
−
m
)
W
N
−
n
(
k
−
m
)
)
=
∑
m
=
0
M
−
1
V
(
m
)
W
N
−
n
m
(
∑
k
=
m
m
+
N
−
1
U
(
k
−
m
)
W
N
−
n
(
k
−
m
)
)
≈
∑
m
=
0
N
−
1
v
(
m
)
W
N
−
n
m
u
n
≈
u
n
∑
m
=
0
N
−
1
v
(
m
)
W
N
−
n
m
≈
u
n
v
n
.
.
.
D
F
T
(
u
n
v
n
)
=
∑
n
=
0
N
−
1
u
n
v
n
W
N
k
n
≈
∑
m
=
0
N
−
1
U
(
k
−
m
)
V
(
m
)
begin{aligned} x_n &= sum_{k=0}^{N-1}W^{-kn}_{N}left( sum_{m=0}^{M-1} U(k-m)V(m) right) \ &= sum_{m=0}^{M-1}V(m)W^{-nm}_{N}left( sum_{k=0}^{N-1} U(k-m)W^{-n(k-m)}_{N} right) \ &= sum_{m=0}^{M-1}V(m)W^{-nm}_{N}left( sum_{k=m}^{m+N-1} U(k-m)W^{-n(k-m)}_{N} right) \ & approx sum_{m=0}^{N-1}v(m)W^{-nm}_{N}u_n \ & approx u_n sum_{m=0}^{N-1}v(m)W^{-nm}_{N} \ & approx u_nv_n \ ...\ DFT(u_nv_n) &= sum_{n=0}^{N-1}u_nv_nW^{kn}_{N} approx sum_{m=0}^{N-1} U(k-m)V(m) end{aligned}
xn...DFT(unvn)=k=0∑N−1WN−kn(m=0∑M−1U(k−m)V(m))=m=0∑M−1V(m)WN−nm(k=0∑N−1U(k−m)WN−n(k−m))=m=0∑M−1V(m)WN−nm(k=m∑m+N−1U(k−m)WN−n(k−m))≈m=0∑N−1v(m)WN−nmun≈unm=0∑N−1v(m)WN−nm≈unvn=n=0∑N−1unvnWNkn≈m=0∑N−1U(k−m)V(m)
与上一节推导类似 ,这里
∑
k
=
m
m
+
N
−
1
U
(
k
−
m
)
W
N
−
n
(
k
−
m
)
sum_{k=m}^{m+N-1} U(k-m)W^{-n(k-m)}_{N}
∑k=mm+N−1U(k−m)WN−n(k−m)也是抽取 k=0,1,2,…N-1-m 的频普(N-m个),补充m个零幅值频率点再做傅里叶逆变换,所以也就是约等于
u
n
u_n
un(一些高频频率丢失),当卷积点数远小于频率数量时,这个约等于是成立的(V(k)也要在后面填充N-M个零)。
结论:对两组离散数据相乘,相当于其两组数据频域作卷积,也就是起到频域数据滤波的效果
DFT与窗函数
由上一个公式可知道,离散数字的乘积与傅里变换后卷积的关系,
u
n
v
n
≈
C
o
n
v
o
l
v
e
(
U
(
k
)
,
V
(
k
)
)
u_nv_n approx Convolve(U(k),V(k))
unvn≈Convolve(U(k),V(k)),
窗函数v与原始数据u相乘后为x,x的频域数据相当于u的频域数据做了一个卷积后的结果
用python 做一下实验
import numpy as np
import math
%pylab inline
data = np.random.randn(64) #尺寸应该为2的次方
kernel = np.array([0.2,0.5,0.2])
convres = np.convolve(data,kernel,'same') #卷积后的结果
dataft = np.fft.fft(data) #原始数据傅里叶结果
kernelft = np.fft.fft(np.pad(kernel,(0,data.size-kernel.size),'constant')) #卷积核傅里叶结果 (填充0 使其与原始数据长度一致)
convresft = np.fft.fft(convres) #卷积后数据傅里叶结果
approx_times = kernelft*dataft #原始数据傅里叶变换与卷积核傅里叶变换相乘结果
div = convresft/(approx_times+1e-10)
div:np.ndarray
#可以看到 kernelft*dataft 与 convresft是比较接近的,(幅值很相近 可能相位相差大一点)
print('可以看到 kernelft*dataft 与 convresft是比较接近的,(幅值很相近 可能相位相差大一点)')
print('幅值比 = ',np.abs(div))
print('相位比 = ',np.angle(div))
可以看到 kernelft*dataft 与 convresft是比较接近的,(幅值很相近 可能相位相差大一点)
幅值比 = [ 1.08514358 1.10805967 0.95296099 1.03198588 0.87026809 0.99448745
1.00526948 0.95799491 1.05421725 1.29726256 0.80609292 0.88131322
0.91631737 1.03311114 0.82737111 0.86807867 1.42545673 0.56157421
0.91429024 1.11167318 0.91778763 1.11124952 1.14813349 0.95219242
1.05733615 0.97868321 1.23478938 1.42048091 1.14337804 2.09690390
2.00851084 12.23768621 1.64446639 12.23768621 2.00851084 2.09690390
1.14337804 1.42048091 1.23478938 0.97868321 1.05733615 0.95219242
1.14813349 1.11124952 0.91778763 1.11167318 0.91429024 0.56157421
1.42545673 0.86807867 0.82737111 1.03311114 0.91631737 0.88131322
0.80609292 1.29726256 1.05421725 0.95799491 1.00526948 0.99448745
0.87026809 1.03198588 0.95296099 1.10805967]
相位比 = [ 0.00000000 0.20103405 0.28134838 0.21410434 0.41299861 0.41863674
0.73898843 0.64316977 0.74492692 0.78055698 1.08688623 0.98047538
1.14141382 1.17736177 1.37149334 1.44358457 1.38108547 1.87904898
1.75100384 1.82650733 1.70435237 1.78623087 2.11383998 1.87868604
2.14499912 2.06628397 2.81174815 3.10020892 2.29021613 -2.58993841
3.12919688 -1.20352958 3.14159265 1.20352958 -3.12919688 2.58993841
-2.29021613 -3.10020892 -2.81174815 -2.06628397 -2.14499912 -1.87868604
-2.11383998 -1.78623087 -1.70435237 -1.82650733 -1.75100384 -1.87904898
-1.38108547 -1.44358457 -1.37149334 -1.17736177 -1.14141382 -0.98047538
-1.08688623 -0.78055698 -0.74492692 -0.64316977 -0.73898843 -0.41863674
-0.41299861 -0.21410434 -0.28134838 -0.20103405]
windows = np.ndarray(data.size)
for i in range(windows.size):
windows[i] = 0.5*(1-math.cos(2*math.pi*i/windows.size)) #汉宁窗
dataft = np.fft.fft(data)/data.size #原始数据傅里叶结果 除以尺寸是因为FFT结果是频域幅的N倍
windowsft = np.fft.fft(windows)/windows.size #窗数据傅里叶结果
#windowsft = np.concatenate([windowsft[0:2],windowsft[-2:-1]])# windowsft[0:2] #由于汉宁窗只有前两个频率是有效的
windata = windows * data #经过窗函数后的数据
windataft = np.fft.fft(windata)/windata.size #开窗后 傅里叶变换数据
#conv1res = np.convolve(dataft,windowsft,'same')
#conv1res = np.convolve(dataft,windowsft,'full')[windowsft.size-1:windowsft.size-1+64] #原数据傅里叶变换与窗函数傅里叶变换卷积
conv1res = np.convolve(dataft,windowsft,'full')[0:dataft.size]
div1 = windataft/conv1res
np.set_printoptions(suppress=True)
np.set_printoptions(precision=5)
print('可以看到 windataft 与 conv1res是比较接近的,(幅值很大部分频率位置相近 可能相位相差大一点)')
print('幅值比 = ',np.abs(div1))
print('相位比 = ',np.angle(div1))
可以看到 windataft 与 conv1res是比较接近的,(幅值很大部分频率位置相近 可能相位相差大一点)
幅值比 = [0.58146 1.51554 1.28522 0.97078 1.56031 1.37292 0.97845 1.65274 1.1212
1.66299 0.64529 0.81242 1.39261 1.29182 0.31025 1.21369 1.08077 0.97666
0.57983 1.86432 1.35158 0.82371 4.23688 1.03864 0.78796 0.99415 2.48601
0.7744 1.50276 1.1419 1.02537 0.96125 0.43243 1.09725 1.29529 0.87585
1.30709 1.07283 1.27008 0.36948 1.30446 1.0443 0.71414 1.50539 1.12606
0.97264 1.1533 1.08976 2.0767 0.87196 0.65309 1.43666 0.71085 0.73239
1.17037 1.56127 1.22908 1.19577 1.43997 1.2673 1.01911 1.31521 1.40685
1. ]
相位比 = [ 0. -1.61908 -0.08994 -0.38359 -0.1287 -0.04803 -0.17619 -0.10482
-0.04996 0.45878 -0.67394 0.36607 -0.01151 -0.14093 -1.83447 -0.02431
0.20923 0.17784 0.15037 -0.23009 -0.23083 -0.03418 -2.95075 0.26942
-0.09524 0.59162 -0.55638 0.39722 -0.93279 0.08441 0.56759 -0.13494
1.68964 0.15164 0.75175 -0.26193 0.60153 -0.07737 -0.03958 0.63195
1.05636 -0.13213 0.48739 -0.25624 -0.16226 0.20864 1.42779 0.40813
0.18961 -0.03562 -0.66101 -0.47631 0.97983 -0.46818 0.10568 0.13711
0.09992 -0.47046 -0.14611 0.00341 -0.275 -0.31533 0.0306 0. ]
wewe = np.fft.ifft(conv1res*data.size)
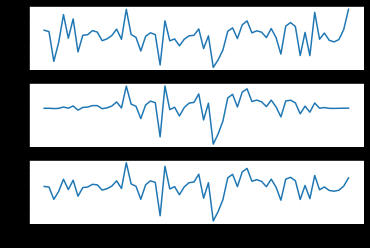
plt.subplot(311)
plt.plot(data) #原始数据波形
plt.subplot(312)
plt.plot(windata) #乘以窗数据后的波形
plt.subplot(313)
plt.plot(np.real(wewe)) #傅里叶结果卷积后 再傳里叶逆变换的波形
最后
以上就是香蕉冰淇淋最近收集整理的关于离散傅里叶 卷积 窗函数 我的理解离散傅里叶与卷积用python 做一下实验的全部内容,更多相关离散傅里叶内容请搜索靠谱客的其他文章。








发表评论 取消回复