cs231n'18： Assignment 3 | LSTM Captioning

Assignment3 | LSTM Captioning

上一节介绍了 Vanilla RNN，同 NN 一样，RNN 存在的最大的问题就是梯度消失。这是因为，RNN 中需要学习的参数在一个 time capsule 结束之后才会更新一次，而在同一个 time capsule 中，所有的时刻都会有 loss 产生，因此也都会有对于参数的梯度产生，最后参数更新时的梯度是所有这些梯度之和。梯度的计算式为：
$$\frac{\partial L}{\partial W}=\sum _{t=1}^T\frac{\partial L^{(t)}}{\partial W}=\sum _{t=1}^T\sum _{k=0}^t\frac{\partial L^{(t)}}{\partial o^{(t)}}\frac{\partial o^{(t)}}{\partial h^{(t)}}\left(\prod _{j=k+1}^t\frac{\partial h^{(j)}}{\partial h^{(j-1)}}\right)\frac{\partial h^{(k)}}{\partial W}$$
通常使用 sigmoid 或者是 tanh 作为激活函数，所以上式中的连乘项可以写成：
$$\prod _{j=k+1}^t\frac{\partial h^{(j)}}{\partial h^{(j-1)}}=\prod _{j=k+1}^t{\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}}^{{}^{\prime }}\cdot W^{t-j}$$
或者
$$\prod _{j=k+1}^t\frac{\partial h^{(j)}}{\partial h^{(j-1)}}=\prod _{j=k+1}^t{\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{m}\mathrm{o}\mathrm{i}\mathrm{d}}^{{}^{\prime }}\cdot W^{t-j}$$
因为$\tanh (x)\in (-1,1)$, 所以 ${\tanh }^{\prime }(x)=1-{\tanh }^2(x)\in (0,1]$;

因为$\sigma (x)\in (0,1)$, 所以 ${\sigma }^{\prime }(x)=\sigma (x)\cdot (1-\sigma (x))\in (0,0.25]$。

所以上述连乘一个小于1的数时，最终会造成梯度的消失。特别是 sigmoid 函数作为激活函数时。

那么，可不可以用 ReLU 函数作激活函数呢？其实是可以的，而且也有很多人在用 ReLU 作 RNN 的激活函数，但是 ReLU 也有自身的缺点。
ReLU 函数的导数要么是 0，要么是 1,。如果是0的话，因为是连乘，所以该时刻以及之前的梯度就一直为 0 了，那么神经元就死掉了。如果 ReLU 的导数在取 1 的范围内的话，连乘中包含一项 W, 在 RNN 的一个 time capsule 中，W 是不变的，只要 W 中有大于 1 的特征值，那么这个连乘就会导致一个数值很大的矩阵；这不像在 CNN 中，随梯度向后传递的 W 是独立的，各个 W 的特征值不会同时大于1或者小于1，所以很大程度上会抵消梯度爆炸的结果。
上述两点实际上都有办法解决。真正选择使用 LSTM 而不用 ReLU 的原因并不是因为梯度消失的问题，而是 LSTM 可以引入长期的记忆，即可以学习长距离的依存关系。

LSTM原理

由于梯度消失，Vanilla RNN 仅有短期记忆，而 LSTM 通过 memory cell 控制引入了长期记忆。

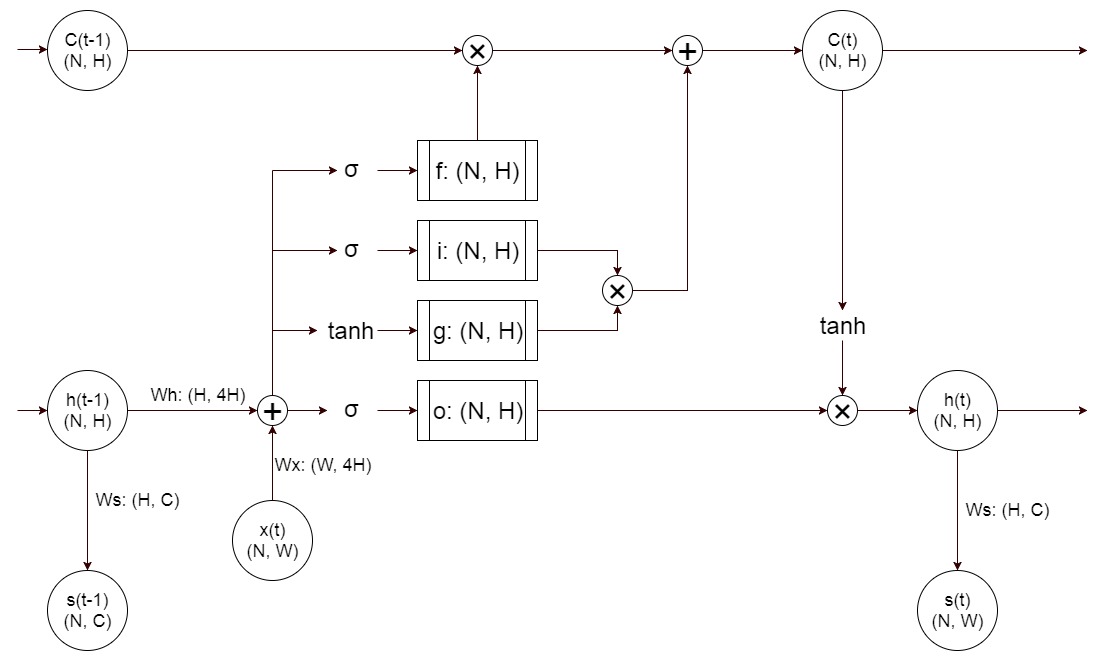
如图所示，与传统的 RNN 相比，LSTM 除了包含原有的 hidden state 以外，还增加了随时间更新的 memory cell。某一时刻的 cell 与 hidden state 有着相同的形状，两者相互依赖于彼此进行状态的更新。具体来看，需要学习的参数 $W_x$ 和 $W_h$ 由 RNN 中的形如 (W, H) 和 (H, H) 变成了 (W, 4H) 和 (H, 4H)，即 (W, f+i+g+o) 和 (H, f+i+g+o)，而 $h(t-1)\cdot W_h+x(t)\cdot W_x$ 的结果也成为形如 (N, f+i+g+o)，其中 f/i/g 用来更新 cell 的状态，得到的新的 cell 状态 C(t) 与 o 一起来更新 h(t)。

forget gate

forget gate 是经过一个 sigmoid 函数得到的，所以它的范围在 (0, 1) 之间，并与 C(t-1) 相乘。它的作用是从前一个 cell 中取多少内容放到新的 cell 中去。这里叫 forget gate，我觉着还不如叫 remember gate 合适。

gate gate

gate gate 是把新的变换结果经过一个 tanh 函数得到的，它实际上是产生了一组新的记忆。

input gate

input gate 是经过一个 sigmoid 函数得到的，所以它的范围在 (0, 1) 之间，并与 gate gate 产生的新的记忆相乘。它的作用是决定新的记忆中有多少内容会被写到新的 memory cell 中去。

新的 memory cell 中的内容由先前cell，forget gate，gate gate 和 input gate 共同决定，即
$$C(t)=C(t-1)\cdot f+i\cdot g$$

output gate

output gate 经过 sigmoid 函数，与经过 tanh 函数的新的记忆 cell 相乘，得到的记过即为新的 hidden state。即：
$$h(t)=o\cdot \tanh (C(t))$$

Affine layer

产生 score 以及 loss 的 affine layer 与 RNN 相同，这里不再赘述。

LSTM 代码实现

LSTM step forward

没什么好说的。

LSTM step backward

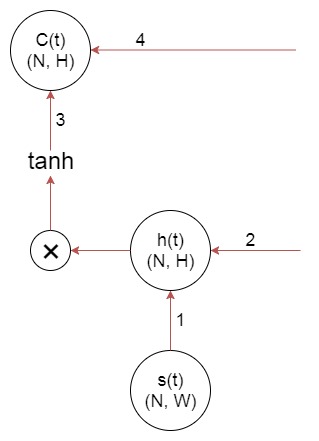
在写 backprop 时，需要注意的是梯度分别沿着两条路径流经 hidden state h(t) 和 cell state C(t)。

对于 h(t) 来说，路径 1 是从 loss 传递下来的梯度，这里并没有给出来；路径 2 是从下一 hidden state 传递下来的梯度，也就是这里的输入参数 dcurrent_h。

对于 C(t) 来说，路径 3 是从此时刻的 h(t) 传递过来的梯度，是需要通过计算得到的；路径 4 是从下一 cell 传递过来的梯度，也就是这里的输入参数 dcurrent_c。所以

Dcurrent_c = dcurrent_h * output_gate * de_tanh(current_c)
Dcurrent_c +=  dcurrent_c

LSTM forward

这里要注意的是，作业里很清楚地说了，初始的 hidden state 作为参数 h0 传递给函数；而初始的 cell state 为0。而且 cell state 作为 LSTM 的内部变量是不返回的。

LSTM backward

函数的输出参数 dout 实际上就是上图中路径 1 在各个时刻的值，所以不要忘记

dcurrent_h += dout[:, i, :]

路径 2,3,4 的值都可以在 lstm_step_backward 中计算出来。

另外，在最终 T 状态，由下一 hidden state 和 cell state 传递过来的梯度都是0。

Inline Question

Recall that in an LSTM the input gate i , forget gate f, and output gate o are all outputs of a sigmoid function. Why don’t we use the ReLU activation function instead of sigmoid to compute these values? Explain.

forget gate 的作用是从上一个 cell state 中拿多少信息放到新的 cell state 中，input gate 的作用是从新生产的状态中拿多少放到新的 cell state 中，output gate 的作用是从上一个 hidden state 拿多少信息来产生新的 hidden state。上述三个门的作用是确定拿 多少，所以门控的输出应该在 (0, 1) 之间，因此要用 sigmoid 函数。如果用 ReLU 的话，就成了将原始的信号放大多少倍了。

output gate 使用的是 tanh 函数，可以用 ReLU 取代。不用 ReLU 的原因大概有：首先由于 W 的连乘，容易梯度爆炸；其次，ReLU 的主要作用就是防止梯度消失，而 LSTM 的主要作用也是防止梯度的消失，所以 ReLU 就没有必要再用了。

GRU: Gated Recurrent Unit

GRU 作为 LSTM 的一种变体，用的也比较多，这里也写一下。与 LSTM 相比，GRU 有两个门：update gate z(t) 和 reset gate r(t)。这两个门的输入都是 h(t-1) 和 x(t)，所以 $W_x$ 是形如 (W, 2H) 的，而 $W_h$ 是形如 (H, 2H)的。两者都是通过 sigmoid 函数得到的：
$$z_t,r_t=\sigma (W_h\cdot h(t-1)+W_x\cdot x(t)+b)$$

随后，用 r(t) 和 h(t-1)，x(t) 产生一个新的中间 hidden state ${\tilde{h}}_t$：
$${\tilde{h}}_t=\tanh (W_{\tilde{h}}\cdot (r_t\ast h(t-1))+W_{\tilde{x}}\cdot x(t))$$
这里可以看出，reset gate 的作用是从上一个 hidden state 中取多少出来用来产生新的中间状态。

最后，下一时刻的 hidden state 由 update gate，h(t-1) 和中间态 ${\tilde{h}}_t$ 共同决定：
$$h(t)=(1-z_t)\ast h(t-1)+z_t\ast {\tilde{h}}_t$$
这里可以看出，update gate $z_t$ 的作用是从上一个 hidden state 和 中间态各取多少信息来构成新的 hidden state。

GRU 的代码实现也写在作业里面了。

最后

以上就是激动苗条为你收集整理的cs231n'18： Assignment 3 | LSTM Captioning的全部内容，希望文章能够帮你解决cs231n'18： Assignment 3 | LSTM Captioning所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。