Abstract
本文介绍了用于VI-SLAM和视觉惯性标定的通用连续时间框架。我们展示了如何使用与传感器的torque-minimal motion密切匹配的样条参数化。与传统的离散时间解决方案相比,连续时间公式对于解决高帧率传感器和多个不同步设备的问题特别有用。我们通过准确建立多个不同步设备的相对姿态和内参,证明了该方法在多传感器视觉惯性SLAM和校准中的适用性。我们还通过对视觉、视惯融合SLAM系统中的全局和滚动快门相机进行评估和统一处理,展示了该方法的优势。
1. Introduction
在本文中,我们描述了一种使用廉价传感器(如卷帘快门相机和MEMS IMU)稳健地执行SLAM的方法。我们针对相机的轨迹使用了连续时间模型,这使我们能够融合来自许多未同步且(可能)具有高速率的传感器的信息,同时限制状态大小。我们对摄像机的卷帘快门进行了建模(Figure1),并且在惯性测量中会生成误差。该模型不仅限于视觉惯性SLAM,还可以简化集成其他传感器(例如SICK激光传感器)。
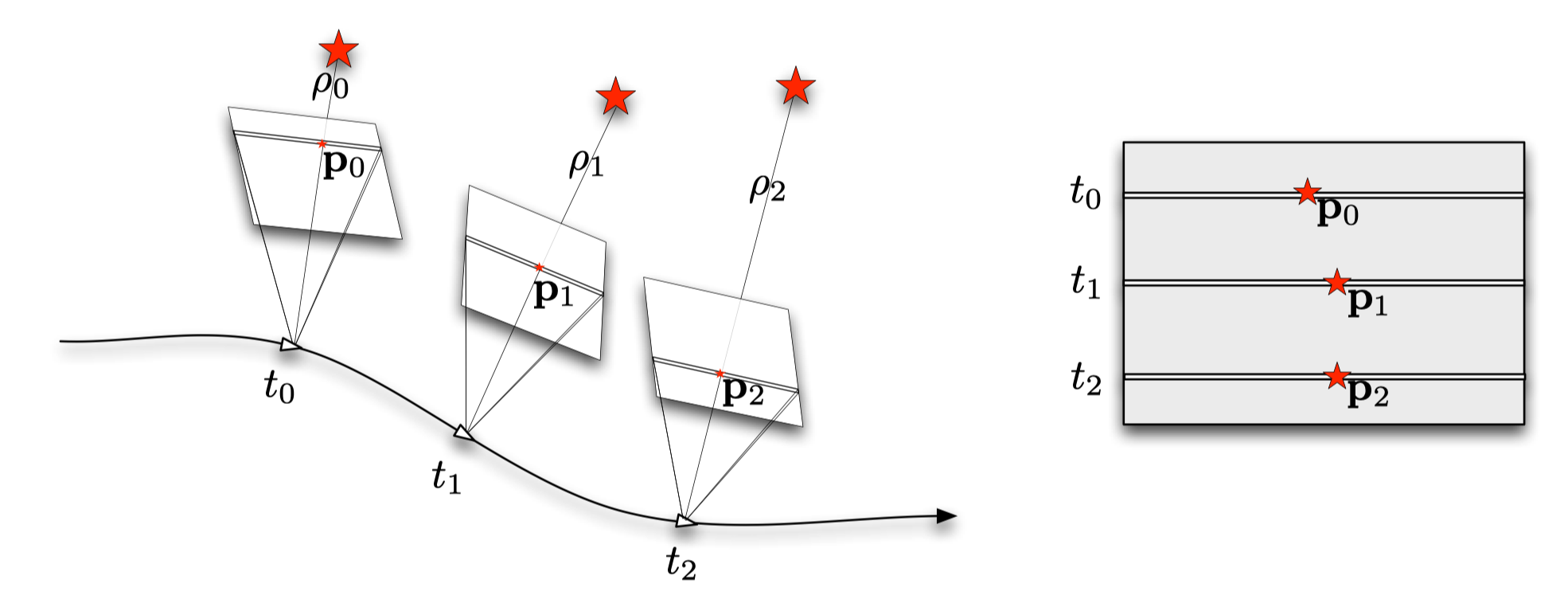
Figure1:通过连续时间SLAM可以很容易的对卷帘相机进行建模。其中在像素位置 p i p_i pi观察到的地标由其反深度 ρ i rho_i ρi表示,测量时间由 t i t_i ti表示。每条扫描线实际上是一个push-broom camera(左);这样的scanline-camera测量值会随时间捕获,这定义了实际传感器返回的图像(右)。
我们方法的另一个重要应用是不同步的多传感器内、外参最小二乘校准。通过定义连续时间模型中所有传感器的姿态,可以联合估算所有传感器参数,包括一些对时间求导的参数,例如陀螺仪和加速度计。通过给定的传感器初值,我们可以得到非常准确的传感器参数。
以前已经提出了许多实时视觉测距和SLAM系统,包括多目系统[6]、[20]、[29],以及单目系统[9]、[18]、[24]、[28]。这些工作都是针对全局快门的相机,也就是说图像中所有的像素点都是在同一时间进行曝光的。针对卷帘快门设备的处理还不成熟,而且主要集中在消除其影响、减少图像失真以构建等价全局快门相机图像方面([][][][][3],[12])。其结果可以用于标准的vSLAM系统中,但是要以将两个优化的过程分离为代价,这有可能导致无法纠正的偏差并增加其处理成本。
Klein等人将PTAM移植到iPhone时,是第一个解决视觉SLAM的滚动快门问题的人。 他们使用连续图像上的特征轨迹来估计每个关键帧的瞬时旋转速度,并以此来预测对测量的一阶校正。Hedborg等人提出了一个非常相似的模型,但是其明确的表示将其嵌入到了卷帘相机的调整当中。他们通过相机的位姿表示模拟了在视频序列中的效果同时将 l l l行当作其相邻 k e y p o s e s key poses key poses的线性插值。
单目视觉SLAM带来了另一个问题,即尺度漂移。当利用单目相机观测路标时,其重建是基于某一未知尺度的,这个尺度通常由初始化过程给定。当相机移动的时候,单目系统会产生尺度漂移和位姿漂移,因为它们无法被直接观测到,最终只能通过一系列的测量将其固定在一个某一个值。Strasdat等人建议当进行闭环、图形松弛(Subsequent Graph Relaxations)等操作时,将这个尺度作为一个显式参数[28]。
解决尺度漂移的另一种方法是使用能够测量绝对尺度的设备来进行扩展。Nuetzi等人,在EKF和样条拟合方法中进行了尺度校正的比较,尽管样条方法中不能进行优化么,但是其可以调整尺度以匹配IMU信息[25]。Kelly等人证明了标定过程中的尺度可观性[14]。在[13]中对此问题进行不同的可观察性分析。他们提出了一个鲁棒的EKF,可以同时校准系统和合并测量值。文献[22]提出了一种类似的基于滤波器的视觉惯性标定方法,该方法基于李导数提供了可观察性分析。此方法需要标定物(标定板?),但可以达到很高的准确性。
上述的所有方法利用的都是离散时间表示。[4]中介绍了一种用于SLAM系统的基于2D样条的连续轨迹表示,其中样条用于表示跟踪对象的轨迹,从而大大减少了状态空间。与我们的方法更接近的是[10],其中使用了连续时间表示法。与我们的方法一样,他们的方法基于车辆轨迹的样条曲线表示。旋转和平移分量由独立的样条曲线参数化。作者测试了他们的相机-IMU校准方法,但需要已知的地标坐标。我们的方法采用了更好的旋转-平移的样条曲线参数化,并且我们还提出了仅使用从校准图案中提取的特征轨迹进行联合视觉惯性自校准的框架。
2. Continuous-time representation
Furgale等人证明了通过使用连续时间表示,可以显著的减少参数数量,并且视觉/惯性目标可以归一为在最小二乘问题。尽管这是一个很好的概念证明,但是由于不能选择使用Cayley-Gibbs-Rodrigues公式对姿势进行参数化然后在该空间中进行插值,因此该表示并不能使其使用样条线进行精确表示。这种表示有几个缺点:
- 在180°具有奇点
- 此空间中的插值不会反映旋转组中的最小距离
- 它不能很好地近似扭矩最小轨迹( torque-minimum trajectories)
相反,我们选择 S E 3 mathbb{SE3} SE3上的Lie代数 s e 3 mathfrak{se3} se3,以便在刚体平移和旋转的流形空间中进行平滑轨迹运动,但是我们只在局部进行,而不是在整体框架中进行。该参数化没有任何奇异之处,并为最小的转矩轨迹提供了很好的解析近似。进一步说明将在2.2节中说明。
2.1 Camera pose transformations
我们通过4 x 4矩阵表示相机之间的位姿转换关系。 例如
T
b
,
a
mathbf{T}_{b,a}
Tb,a表示帧a到b的变换矩阵。因此
x
b
∝
T
b
,
a
x
a
mathbf{x}_bpropto mathbf{T}_{b,a}mathbf{x}_a
xb∝Tb,axa。我们可以将
T
b
,
a
mathbf{T}_{b,a}
Tb,a分解为如下形式
T
b
,
a
=
[
R
b
,
a
a
b
0
T
1
]
,
T
b
,
a
∈
S
E
3
,
R
b
,
a
∈
S
O
3
begin{aligned} mathbf{T}_{b,a}= begin{bmatrix} mathbf{R}_{b,a} & mathbf{a}_b \ mathbf{0}^T & 1 end{bmatrix}, mathbf{T}_{b,a}in mathbb{SE3}, mathbf{R}_{b,a} in mathbb{SO3} end{aligned}
Tb,a=[Rb,a0Tab1], Tb,a∈SE3, Rb,a∈SO3
其中 R b , a mathbf{R}_{b,a} Rb,a是是3×3正交旋转矩阵,表示帧a和b之间的纯旋转。 a b mathbf{a}_b ab表示在 b b b坐标系下 a a a的位置。如果 T b , a mathbf{T}_{b,a} Tb,a表示在时间 Δ t Delta t Δt内两坐标系 T w , a , T w , b mathbf{T}_{w,a},mathbf{T}_{w,b} Tw,a,Tw,b之间的变换(其中 w w w代表世界坐标系),运动过程中角速度和线速度恒定。线速度我们可以用矩阵形式表示为 Ω = 1 Δ t log T b , a , Ω ∈ R 4 × 4 Omega=frac{1}{Delta t}log_{}{mathbf{T}_{b,a}},Omega inmathbb{R}^{4times4} Ω=Δt1logTb,a,Ω∈R4×4,其中log是矩阵的对数。对于 S E 3 mathbb{SE3} SE3,对数映射和指数映射可以以封闭形式计算[27]。
2.2 C 2 C^2 C2 -continuous curves in S E 3 mathbb{SE3} SE3
我们方法的核心是连续的轨迹表示。我们选择了一种表达法,它提供:
- 本地控制,使系统既可以在线运行也可以批量运行
- C 2 C^2 C2连续性使我们能够预测IMU测量
- 最小torque trajectories的良好近似值
我们知道,三次样条差值能够很好的被应用在三维上。但是并不容易被用于处理3D旋转(例如 S O 3 mathbb{SO3} SO3上的插值)。例如, C 2 C^2 C2的连续性不一定被保留[15]。我们选择利用类似[8]中提出的利用李代数形式的cumulative basis functions进行参数化。在计算机动画方面,在[16]中首次提出了使用累积B样条基函数进行四元数插值的方法。这种表示不仅是连续的 C 2 C^2 C2,而且还提供了非常简单的二阶导数公式。
2.2.1 Representing B-Splines with cumulative basis functions
k
−
1
k-1
k−1维的B样条曲线的标准基函数表示为:
p
(
t
)
=
∑
i
=
0
n
p
i
B
i
,
k
(
t
)
mathbf{p}(t)=sum_{i=0}^nmathbf{p}_iB_{i,k}(t)
p(t)=i=0∑npiBi,k(t)
其中
p
i
∈
R
N
mathbf{p}_i in mathbb{R}^N
pi∈RN是在时间点
t
i
t_i
ti的控制点,
i
∈
[
0
,
.
.
.
,
n
]
iin[0,...,n]
i∈[0,...,n]。
B
i
,
k
(
t
)
B_{i,k}(t)
Bi,k(t)是基础方程,可以使用De Boor - Cox递归方程进行计算[5]、[7]。方程(1)可以重组为以下形式的累积形式:
p
(
t
)
=
p
0
B
~
0
,
k
(
t
)
+
∑
i
=
1
n
(
p
i
−
p
i
−
1
B
~
i
,
k
(
t
)
)
mathbf{p}(t)=mathbf{p}_0tilde{B}_{0,k}(t)+sum_{i=1}^n(mathbf{p}_i-mathbf{p}_{i-1}tilde{B}_{i,k}(t))
p(t)=p0B~0,k(t)+i=1∑n(pi−pi−1B~i,k(t))
其中
B
~
i
,
k
(
t
)
=
∑
j
=
i
n
B
j
,
k
(
t
)
tilde{B}_{i,k}(t)=sum_{j=i}^nB_{j,k}(t)
B~i,k(t)=∑j=inBj,k(t)是累积基函数(cumulative basis functions)。利用上一节中描述的对数和指数映射,我们可以通过指数映射
Ω
i
=
log
(
T
w
,
i
−
1
−
1
T
w
,
i
)
∈
s
e
3
Omega_i=log{(mathbf{T}^{-1}_{w,i-1}mathbf{T}_{w,i})}inmathfrak{se3}
Ωi=log(Tw,i−1−1Tw,i)∈se3代替控制点之间的的点差来重写公式(2)来描述
S
E
3
mathbb{SE3}
SE3上的轨迹:
T
w
,
s
(
t
)
=
exp
(
B
~
0
,
k
(
t
)
log
(
T
w
,
0
)
)
∏
i
=
1
n
(
exp
(
B
~
i
,
k
(
t
)
Ω
)
i
)
mathbf{T}_{w,s}(t)=exp{(tilde{B}_{0,k}(t)log{(mathbf{T}_{w,0})})prod_{i=1}^n(exp(tilde{B}_{i,k}(t)Omega)_i)}
Tw,s(t)=exp(B~0,k(t)log(Tw,0))i=1∏n(exp(B~i,k(t)Ω)i)
其中
T
w
,
s
(
t
)
∈
S
E
3
mathbf{T}_{w,s}(t)inmathbb{SE3}
Tw,s(t)∈SE3是时间
t
t
t处沿样条线的位姿,
T
w
,
i
∈
S
E
3
mathbf{T}_{w,i}inmathbb{SE3}
Tw,i∈SE3是控制位姿(control poses)。我们使用下标
w
w
w来强调时间点
t
t
t的位姿、控制位姿都是基于世界坐标系下的。
2.2.2 Cumulative cubic B-Splines
在本文中,我们关注于累积三次B样条曲线(
k
=
4
k=4
k=4)的特殊情况。我们假设控制点以均匀的时间间隔
Δ
t
Delta t
Δt分布。在三次B样条曲线中,在时间
t
t
t处四个控制点影响样条曲线的值。我们将这些控制点定义为
[
t
i
−
1
,
t
i
,
i
i
+
1
,
t
i
+
2
]
,
t
∈
[
t
i
,
t
i
+
1
]
[t_{i-1},t_i,i_{i+1},t_{i+2}], tin [t_i,t_{i+1}]
[ti−1,ti,ii+1,ti+2], t∈[ti,ti+1]这样一个集合。我们可以通过使用统一的时间表示
s
(
t
)
=
(
t
−
t
0
)
/
Δ
t
s(t)=(t-t_0)/Delta t
s(t)=(t−t0)/Δt来进一步简化表示法。这将控制点时间
t
i
t_i
ti转换为统一时间
s
i
∈
[
0
,
1
,
.
.
.
,
n
]
s_iin[0,1,...,n]
si∈[0,1,...,n]。对于给定的时间
s
i
≤
s
(
t
)
≤
s
i
+
1
s_ileq s(t)leq s_{i+1}
si≤s(t)≤si+1,我们定义
u
(
t
)
=
s
(
t
)
−
s
i
u(t)=s(t)-s_i
u(t)=s(t)−si。使用这种时间公式,并基于De Boor-Cox公式的矩阵表示[26],我们可以写出累积基数
B
~
(
u
)
tilde{mathbf{B}}(u)
B~(u)及其时间导数
B
~
˙
(
u
)
,
B
~
¨
(
u
)
dot{tilde{mathbf{B}}}(u), ddot{tilde{mathbf{B}}}(u)
B~˙(u), B~¨(u)为:
B
~
(
u
)
=
C
[
1
u
u
2
u
3
]
,
B
~
˙
(
u
)
=
1
Δ
t
C
[
0
1
2
u
3
u
2
]
,
B
~
¨
(
u
)
=
1
Δ
t
2
C
[
0
0
2
6
u
]
,
C
=
1
6
[
6
0
0
0
5
3
−
3
1
1
3
3
−
2
0
0
0
1
]
begin{aligned} tilde{mathbf{B}}(u)=mathbf{C} begin{bmatrix} 1\u\u^2\u^3 end{bmatrix},quad dot{tilde{mathbf{B}}}(u)=frac{1}{Delta t}mathbf{C} begin{bmatrix} 0\1\2u\3u^2 end{bmatrix},quad ddot{tilde{mathbf{B}}}(u)=frac{1}{Delta t^2}mathbf{C} begin{bmatrix} 0\0\2\6u end{bmatrix} ,quad mathbf{C}=frac{1}{6} begin{bmatrix} 6 &0&0&0\ 5&3&-3&1\ 1&3&3&-2\ 0&0&0&1 end{bmatrix} end{aligned}
B~(u)=C⎣⎢⎢⎡1uu2u3⎦⎥⎥⎤,B~˙(u)=Δt1C⎣⎢⎢⎡012u3u2⎦⎥⎥⎤,B~¨(u)=Δt21C⎣⎢⎢⎡0026u⎦⎥⎥⎤,C=61⎣⎢⎢⎡651003300−33001−21⎦⎥⎥⎤
现在可以将样条轨迹中的位姿定义为:
T
w
,
s
(
u
)
=
T
w
,
i
−
1
∏
j
=
1
3
exp
(
B
~
(
u
)
j
Ω
i
+
j
)
mathbf{T}_{w,s}(u)=mathbf{T}_{w,i-1}prod_{j=1}^3exp(tilde{mathbf{B}}(u)_jmathbf{Omega_{i+j}})
Tw,s(u)=Tw,i−1j=1∏3exp(B~(u)jΩi+j)
第
i
i
i个索引取自定义了
u
(
t
)
u(t)
u(t)的区间的索引,
B
~
(
u
)
j
tilde{mathbf{B}}(u)_j
B~(u)j中的下标索引表示
B
~
(
u
)
tilde{mathbf{B}}(u)
B~(u)的第
j
j
j个元素(基于0的),
Ω
Omega
Ω定义不变。注意,
B
~
(
u
)
0
=
1
,
∀
u
tilde{mathbf{B}}(u)_0=1,forall{u}
B~(u)0=1,∀u。我们可以将位姿关于时间的一阶、二阶导数写为如下形式:
T
˙
w
,
s
(
u
)
=
T
w
,
i
−
1
(
A
˙
0
A
1
A
2
+
A
0
A
˙
1
A
2
+
A
0
A
1
A
˙
2
)
dot{mathbf{T}}_{w,s}(u)=mathbf{T}_{w,i-1} (dot{mathbf{A}}_0mathbf{A}_1mathbf{A}_2 +mathbf{A}_0dot{mathbf{A}}_1mathbf{A}_2 +mathbf{A}_0mathbf{A}_1dot{mathbf{A}}_2)
T˙w,s(u)=Tw,i−1(A˙0A1A2+A0A˙1A2+A0A1A˙2)
T ¨ w , s ( u ) = T w , i − 1 ( A ¨ 0 A 1 A 2 + A 0 A ¨ 1 A 2 + A 0 A 1 A ¨ 2 2 ( A ˙ 0 A 1 ˙ A 2 + A ˙ 0 A 1 A 2 ˙ + A 0 A ˙ 1 A 2 ˙ ) ) ddot{mathbf{T}}_{w,s}(u)=mathbf{T}_{w,i-1} dbinom{ddot{mathbf{A}}_0mathbf{A}_1mathbf{A}_2 +mathbf{A}_0ddot{mathbf{A}}_1mathbf{A}_2 +mathbf{A}_0mathbf{A}_1ddot{mathbf{A}}_2} {2 (dot{mathbf{A}}_0dot{mathbf{A}_1}mathbf{A}_2 +dot{mathbf{A}}_0mathbf{A}_1dot{mathbf{A}_2} +mathbf{A}_0dot{mathbf{A}}_1dot{mathbf{A}_2})} T¨w,s(u)=Tw,i−1(2(A˙0A1˙A2+A˙0A1A2˙+A0A˙1A2˙)A¨0A1A2+A0A¨1A2+A0A1A¨2)
A j = exp ( Ω i + j B ~ ( u ) j ) A ˙ j = A j Ω i + j B ~ ˙ ( u ) j A ¨ j = A ˙ j Ω i + j B ~ ˙ ( u ) j + A j Ω i + j B ~ ¨ ( u ) j begin{aligned} mathbf{A}_j&=exp{(mathbf{Omega_{i+j}}tilde{mathbf{B}}(u)_j)}\ dot{mathbf{A}}_j&=mathbf{A}_jmathbf{Omega_{i+j}}dot{tilde{mathbf{B}}}(u)_j\ ddot{mathbf{A}}_j&=dot{mathbf{A}}_jmathbf{Omega_{i+j}}dot{tilde{mathbf{B}}}(u)_j+mathbf{A}_jmathbf{Omega_{i+j}}ddot{tilde{mathbf{B}}}(u)_j end{aligned} AjA˙jA¨j=exp(Ωi+jB~(u)j)=AjΩi+jB~˙(u)j=A˙jΩi+jB~˙(u)j+AjΩi+jB~¨(u)j
3. Generative model of visual-inertial data
3.1 Parameterization
我们使用沿着样条线的第一次观测的逆深度
ρ
∈
R
+
rhoinmathbb{R}^+
ρ∈R+来参数化我们的路标点。已经表明,逆深度能够表示无限远处的点,从而大大简化了单眼特征的初始化[23]。我们可以通过
W
mathcal{W}
W将在帧
a
a
a中观测到的坐标为
p
a
∈
R
2
mathbf{p}_ainmathbb{R^2}
pa∈R2的点转换到
b
b
b帧下的对应坐标
p
b
∈
R
2
mathbf{p}_binmathbb{R^2}
pb∈R2:
p
b
=
W
(
p
a
;
T
b
,
a
,
ρ
)
=
π
(
[
K
b
∣
0
]
T
b
,
a
[
K
a
−
1
[
p
a
1
]
;
ρ
]
)
mathbf{p}_b=mathcal{W}(mathbf{p}_a;mathbf{T}_{b,a},rho)=pileft([mathbf{K}_b|0]mathbf{T}_{b,a}[mathbf{K}_a^{-1} begin{bmatrix} mathbf{p}_a\ 1 end{bmatrix};rho]right)
pb=W(pa;Tb,a,ρ)=π([Kb∣0]Tb,a[Ka−1[pa1];ρ])
其中
π
(
P
=
1
P
2
[
P
0
,
P
1
]
T
)
pi(mathbf{P}=frac{1}{mathbf{P}_2}[mathbf{P}_0,mathbf{P}_1]^T)
π(P=P21[P0,P1]T)是齐次投影函数,
K
a
,
K
b
∈
R
3
×
3
mathbf{K}_a,mathbf{K}_binmathbb{R^{3times3}}
Ka,Kb∈R3×3分别代表帧
a
,
b
a,b
a,b的内参。
累积B样条参数化使我们能够计算时间导数的表达形式,如第2.2.2节所示。这使我们可以轻松地合成加速度计和陀螺仪的测量结果,进而可以用来在观测到的测量结果上形成误差。
G
y
r
o
(
u
)
=
R
w
,
s
T
(
u
)
⋅
R
˙
w
,
s
(
u
)
+
b
i
a
s
Gyro(u)=mathbf{R}^T_{w,s}(u)·dot{mathbf{R}}_{w,s}(u)+bias
Gyro(u)=Rw,sT(u)⋅R˙w,s(u)+bias
我们使用沿着样条线的第一个观测姿势的反深度ρ∈R +在系统中对地标进行参数化
A
c
c
e
l
(
u
)
=
R
w
,
s
T
(
u
)
⋅
(
s
¨
w
(
u
)
+
g
w
)
+
b
i
a
s
Accel(u)=mathbf{R}^T_{w,s}(u)·(ddot{s}_w(u)+mathscr{g}_w)+bias
Accel(u)=Rw,sT(u)⋅(s¨w(u)+gw)+bias
其中
R
˙
w
,
s
dot{mathbf{R}}_{w,s}
R˙w,s和
s
¨
w
ddot{s}_w
s¨w是分别为
T
˙
w
,
s
dot{mathbf{T}}_{w,s}
T˙w,s和
T
¨
w
,
s
ddot{mathbf{T}}_{w,s}
T¨w,s的子矩阵(如第2.1节所定义),而
g
w
mathscr{g}_w
gw是在世界坐标系中由于重力引起的加速度。
3.2 Minimization
通过给定的视觉和惯性数据生成模型,我们可以通过最小化目标函数(最小化测量值和观测值之差),来批量或在窗口范围内求解样条曲线和摄像机参数。通过使用连续时间公式,我们可以对重投影误差和惯性误差进行校准,并通过设备规格或校准中计算出的信息矩阵
∑
sum
∑对其进行加权。当我们收到新的测量值时,我们通过迭代找出
min
θ
E
(
θ
)
min_theta E(theta)
minθE(θ):
E
(
θ
)
=
∑
p
^
m
(
p
^
m
−
W
(
p
r
;
T
c
,
s
T
w
,
s
(
u
m
)
−
1
T
w
,
s
(
u
r
)
T
s
,
c
,
ρ
)
)
∑
p
2
+
∑
ω
^
m
(
ω
^
m
−
G
y
r
o
(
u
m
)
)
∑
ω
2
+
∑
a
^
m
(
a
^
m
−
A
c
c
e
l
(
u
m
)
)
∑
a
2
E(theta)=sum_{hat{mathbf{p}}_m}left(hat{mathbf{p}}_m-mathcal{W}(mathbf{p}_r;mathbf{T}_{c,s}mathbf{T}_{w,s}(u_m)^{-1}mathbf{T}_{w,s}(u_r)mathbf{T}_{s,c},rho)right)^2_{sum_p}\ +sum_{hat{omega}_m}left(hat{omega}_m-Gyro(u_m)right)^2_{sum_omega} +sum_{hat{a}_m}left(hat{a}_m-Accel(u_m)right)^2_{sum_a}
E(θ)=p^m∑(p^m−W(pr;Tc,sTw,s(um)−1Tw,s(ur)Ts,c,ρ))∑p2+ω^m∑(ω^m−Gyro(um))∑ω2+a^m∑(a^m−Accel(um))∑a2
对所有视觉和惯性测量值
p
^
m
,
ω
^
m
,
a
^
m
hat{mathbf{p}}_m,hat{mathbf{omega}}_m,hat{mathbf{a}}_m
p^m,ω^m,a^m(或在滑动窗口内的测量值)求和。测量
m
m
m发生在时刻
u
m
u_m
um。对于逆深度路标的测量值,
u
r
u_r
ur表示首次观察到路标的参考时间。
θ
theta
θ表示要优化的参数矢量(可能因应用而异),包括样条曲线控制姿态,相机内参,路标点的反深度值
ρ
rho
ρ,相机到IMU的转换
T
c
,
s
mathbf{T}_{c,s}
Tc,s和IMU偏差。我们通过迭代非线性最小二乘来实现这一点,这需要对
E
(
θ
)
E(theta)
E(θ)进行线性化处理,找到该近似函数的最小值,更新
θ
theta
θ并重复。我们在
s
e
3
mathfrak{se3}
se3中通过其对应的李代数进一步对姿势变换更新进行参数化,详情参见[27]。我们使用Ceres来求解这个最小二乘问题。
4. Projection into a rolling shutter camera
尽管滚动快门式照相机的投影几何形状与全局快门式照相机的投影几何形状相同,但是图像的每一行都曝光了不同的时间段,每行的延迟时间都比最后一帧的延迟时间长。照相机运动时,这可能会导致图像失真和歪斜(果冻效应)。使用相机的运动的连续时间模型,我们可以自由地将图像的每一行视为其自身的曝光。但是,这样做需要将每个路标分别投影到每条线中。尽管每个像素只有一个曝光时间,我们也可以通过它们周围的图像信息来测量路标点(尽管这些信息可能跨越多条线)。
我们倾向于将y轴视为时间的连续参数化,其中子像素值代表不同的时间间隔。This approximation balances patch measurements that occur over multiple lines。
p
b
(
t
)
=
[
x
b
(
t
)
y
b
(
t
)
]
=
W
(
p
a
;
T
b
,
a
(
t
)
,
ρ
)
mathbf{p}_b(t)= begin{bmatrix} x_b(t)\ y_b(t) end{bmatrix} =mathcal{W}(mathbf{p}_a;mathbf{T}_{b,a}(t),rho)
pb(t)=[xb(t)yb(t)]=W(pa;Tb,a(t),ρ)
首先,由于我们没办法事先知道路标点将在何时、投影到相机中的哪一个位置。Meingast等人对于卷帘相机在不同运动下的匀速运动模型进行了分析,并表明可以在特定情况下来解决这个问题[21]。尽管我们没有假定恒定的速度轨迹,但是我们遵循的方法与它们在一般运动中的投影非常相似。某一时刻的2D观测可以表示为
y
b
(
t
)
=
h
(
t
−
s
)
/
(
e
−
s
)
y_{b(t)}=h(t-s)/(e-s)
yb(t)=h(t−s)/(e−s),其中
s
s
s为帧开始的时间,
e
e
e是帧结束的时间,
h
h
h是图像像素单位的高度。我们可以看出,这个式子中的时间和公式(11)是不匹配的。我们首先在两帧时间间隔内我们认为的最佳y轴位置投影一次地标,也许是从最后一帧初始化的。然后,我们对该路标点的投影进行一阶泰勒展开,并解决为止时间差异:
p
b
(
t
+
Δ
t
)
=
W
(
p
a
;
T
b
,
a
(
t
)
,
ρ
)
+
Δ
t
d
W
(
p
a
;
T
b
,
a
(
t
)
,
ρ
)
d
t
mathbf{p}_b(t+Delta t)=mathcal{W}(mathbf{p}_a;mathbf{T}_{b,a}(t),rho)+Delta tfrac{dmathcal{W}(mathbf{p}_a;mathbf{T}_{b,a}(t),rho)}{dt}
pb(t+Δt)=W(pa;Tb,a(t),ρ)+ΔtdtdW(pa;Tb,a(t),ρ)
y b ( t + Δ t ) = h ( t + Δ t − s ) e − s , Δ t = − h . t 0 + s . ( y b ( t ) − h ) − e . y b ( t ) ( s − e ) d W y ( p a ; T b , a ( t ) , ρ ) d t + h y_{b(t+Delta t)}=frac{h(t+Delta t-s)}{e-s}, Delta t=-frac{h.t_0+s.(y_b(t)-h)-e.y_b(t)}{(s-e)frac{dmathcal{W}_y(mathbf{p}_a;mathbf{T}_{b,a}(t),rho)}{dt}+h} yb(t+Δt)=e−sh(t+Δt−s), Δt=−(s−e)dtdWy(pa;Tb,a(t),ρ)+hh.t0+s.(yb(t)−h)−e.yb(t)
每次迭代,我们设置 t ← t + Δ t tleftarrow t+Delta t t←t+Δt,并重复此步骤。仅经过2到3次迭代,我们就可以高精度地收敛到一致的投影/观察时间,即使对于严重的滚动快门也是如此。
5. Experiments
我们已经在模拟和真实数据中进行了实验,以评估我们灵活的连续时间方法。我们首先展示了利用模拟的单目卷帘快门数据集在滑动窗口视觉里程计的结果。我们将继续在真实数据上演示我们的系统,以实现联合视觉惯性SLAM和自标定。
5.1 Simulated rolling shutter visual odometry
为了解决卷帘式相机的单眼视觉测距法,我们生成了具有严重果冻效应的模拟序列(图2a)。该数据集模拟了一个人快速行走超过200帧的城市街区。对于恒定时间操作,我们考虑三次样条控制点的固定大小的滑动窗口,根据需要添加新的结,并在进行新的视觉界标测量时进行优化。
为了引导系统,我们首先使用[17]中描述的初始化方法。该方法假定的是全局快门相机观测到的路标点,但是作为初始化方法,该方法已足够,尤其是针对相机缓慢移动的情况。这为我们提供了两个选定的初始化帧之间的初始转换,然后可以用来对添加到样条线的特征进行三角剖分。特征点由它们的2D坐标,时间(从像线得出)和在初次看到时的逆深度表示,如第3.1节所述。
捕获新帧时,使用第4节中所述的方法根据样条曲线预测以前观察到的地标的图像投影。根据这些预测,通过使用FREAK描述符[2]对附近特征进行匹配来进行数据关联。对样条的最后N个控制点进行了优化,保留了前三个固定点。每个控制点还包括一个非常弱的运动模型,以有利于低加速度-即使在节距间隔内测量值太少,也可以使样条受到很好的约束。如果匹配的地标数量低于阈值(本例中为64),从当前图像的特征点无限远初始化新的地标,并将其添加到样条线。
图2展示了在模拟滚动快门时以及在根据全局快门相机错误地建模时间时,在模拟序列上操作的方法。当考虑到卷帘快门时时,我们设法恢复了模拟城市街区的结构而没有严重变形(图2b)。忽略卷帘快门的影响,观察到更明显的漂移,并且如预期的那样,当卷帘畸变较大时(即,在拐角处转弯时),估计轨迹中的伪像特别明显。建模卷帘快门时,闭环位置误差(通过行进距离标准化)为0.0057,而全局快门时为0.0472。
最后
以上就是背后金鱼最近收集整理的关于A continuous-time representation for v-i fusion with application to rolling shutter camerasAbstract1. Introduction2. Continuous-time representation3. Generative model of visual-inertial data4. Projection into a rolling shutter camera5. Experiments的全部内容,更多相关A内容请搜索靠谱客的其他文章。







![[kuangbin]数学训练四 数论 [Cloned]](https://www.shuijiaxian.com/files_image/reation/bcimg10.png)
发表评论 取消回复