【MATLAB数字信号处理】离散时间系统的时域分析（三）

2.6 线性时不变系统的级联

​ 在实际应用中，高阶因果线性时不变离散时间系统可以用低阶因果线性时不变离散时间系统级联得到。例如，四阶离散时间系统：

$$y[n]+1.6y[n-1]+2.28y[n-2]+1.325y[n-3]+0.68y[n-4]=0.06x[n]-0.19x[n-1]+0.27x[n-2]-0.26x[n-3]+0.12x[n-4]$$

可用两个二阶离散时间系统的级联实现。

第一级：

$$y_1[n]=0.9y_1[n-1]+0.8y_1[n-2]=0.2x[n]-0.2x[n-1]+0.4x[n-2]$$

第二级：

$$y_2[n]+0.7y_2[n-1]+0.85y_2[n-2]=0.2y_1[n]-0.5y_1[n-1]+0.3y_1[n-2]$$

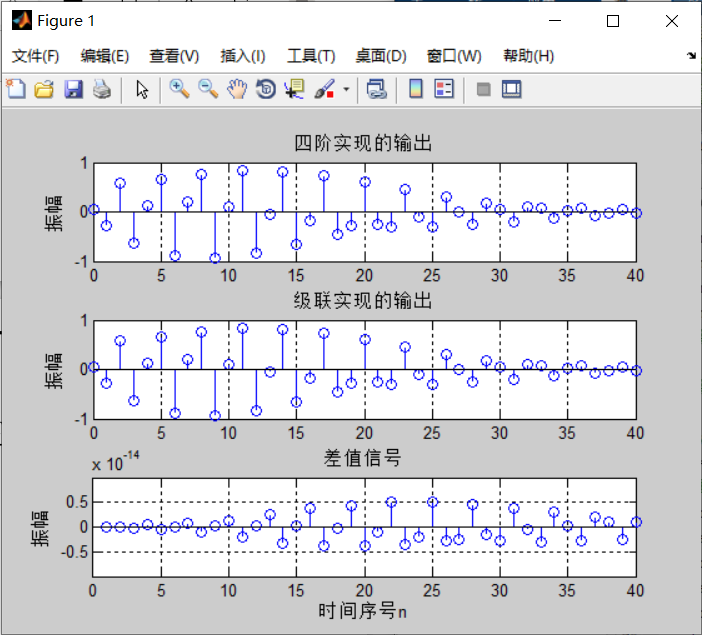
​ 通过MATLAB仿真上述四阶系统和二阶系统。首先产生序列$x[n]$，将其作为四阶系统的输入，生成输出$y[n]$。然后将同样的输入$x[n]$应用到第一级得到输出序列$y_1[n]$。接下来用$y_1[n]$作为第二级的输入得到它的输出$y_2[n]$。最后求出$y_1[n]$和$y_2[n]$之间的差，并画出所有的输出信号和差值信号。

% 线性时不变系统的级联实现
clf;
x = [1,zeros(1,40)];  % 生成输入
n = 0:40;
% 四阶系统的系数
den = [1 1.6 2.28 1.325 0.68];
num = [0.06 -0.19 0.27 -0.26 0.12];
% 计算四阶系统的输出
y = filter(num,den,x);
% 两个二阶系统的系数
num1 = [0.3 -0.2 0.4];
den1 = [1 0.9 0.8];
num2 = [0.2 -0.5 0.3];
den2 = [1 0.7 0.85];
% 级联第一级的输出y1[n]
y1 = filter(num1,den1,x);
% 级联第二级的输出y2[n]
y2 = filter(num2,den2,y1);
% y[n]和y2[n]之间的差
d = y - y2;
% 画出输出和差值信号
subplot(3,1,1);stem(n,y);
ylabel('振幅');title('四阶实现的输出');grid;
subplot(3,1,2);stem(n,y2);
ylabel('振幅');title('级联实现的输出');grid;
subplot(3,1,3);stem(n,d);
xlabel('时间序号n');ylabel('振幅');title('差值信号');grid;

2.7 卷积

​ 卷积运算在MATLAB中可以通过命令conv实现。

​ 例如，可以把系统的冲激响应与给定的有限长输入序列进行卷积，得到有限冲激响应系统的输出序列。

% 卷积运算
clf;
h = [3 2 1 -2 1 0 -4 0 3];  % 冲激
x = [1 -2 3 -4 3 2 1];  % 输入序列
y = conv(h,x);
n = 0:14;
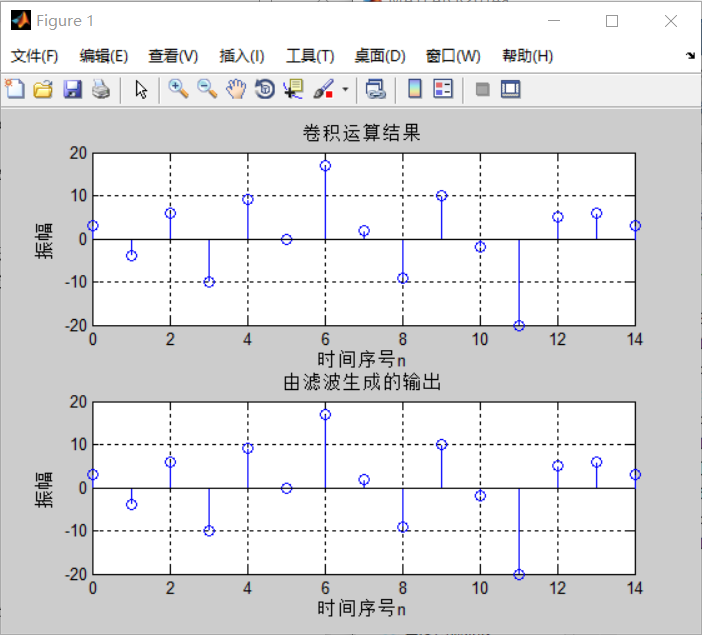
subplot(2,1,1);stem(n,y);
xlabel('时间序号n');ylabel('振幅');title('卷积运算结果');grid;
x1 = [x zeros(1,8)];
y1 = filter(h,1,x1);
subplot(2,1,2);stem(n,y1);
xlabel('时间序号n');ylabel('振幅');title('由滤波生成的输出');grid

2.8 信号的相关

2.8.1 定义

​ 互相关序列$r_{xy}[l]$表示一对能量信号$x[n]$和$y[n]$之间相似性的度量，其定义为（假设式中的无限求和是收敛的）：

$$r_{xy}[l]=\sum _{n=-\infty }^{\infty }x[n]y[n-l],l=0,\pm 1,\pm 2,\dots \dots$$

参数$l$称为时滞，表示这一对信号间的时移。若为正，则说明时间序列$y[n]$相对于参考序列$x[n]$右移了$l$个样本；若为负，则说明时间序列$y[n]$相对于参考序列$x[n]$左移了$l$个样本。

​ 上式中下标$xy$的顺序表明$x[n]$是参考序列，它在时间上保持固定，而序列$y[n]$相对于$x[n]$做平移。若希望$y[n]$做参考序列而序列$x[n]$相对于$y[n]$平移，则相应的互相关序列为：

$$r_{yx}[l]=\sum _{n=-\infty }^{\infty }y[n]x[n-l]=\sum _{m=-\infty }^{\infty }y[m+l]x[m]=r_{xy}[-l]$$

由此可见，$r_{yx}[l]$是序列$r_{xy}[l]$经过时间反转得到的。

​ 令$y[n]$=$x[n]$即可得到序列$x[n]$的自相关序列为：

$$r_{xx}[l]=\sum _{n=-\infty }^{\infty }x[n]x[n-l]$$

2.8.2 信号的相关的应用

2.8.2.1 寻找被噪声淹没的有用信号的位置

​ 利用互相关运算寻找被噪声淹没的有用信号的位置。得到互相关运算的计算结果后，出现峰值的位置即为有用信号在合成信号中的位置，此时可通过MATLAB命令返回峰值和峰值出现的位置，即为被噪声淹没的有用信号的位置。

nx = 20;
x1 = 1:nx;
x = sin((pi/10)*x1);
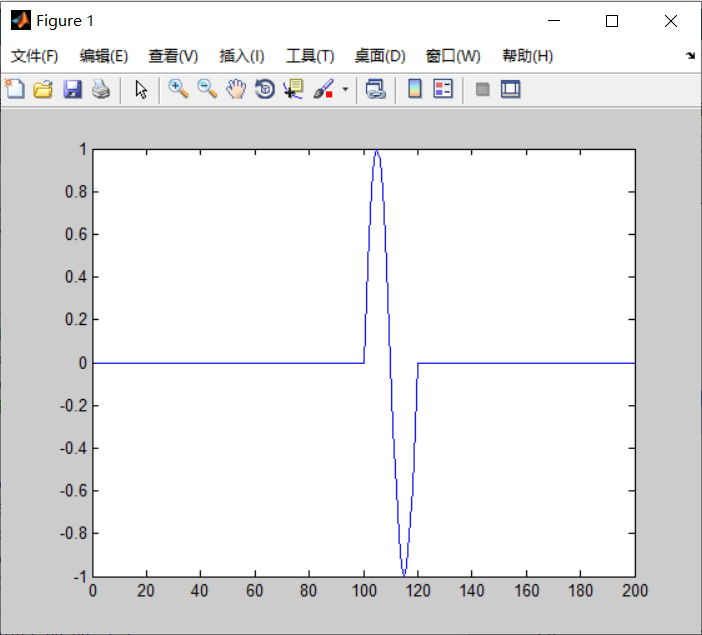
% 构造合成信号
yy = [zeros(1,100),x,zeros(1,80)];
figure(1);plot(yy)
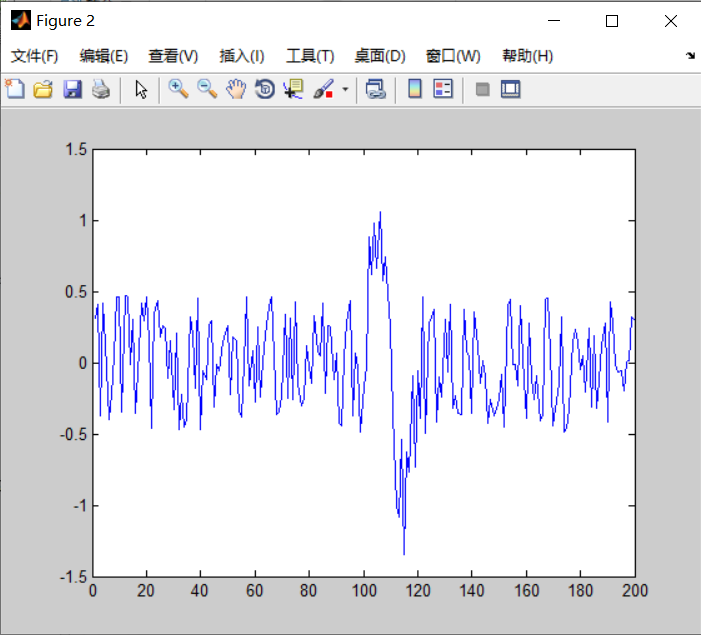
% 添加随机噪声
s = rand(1,200) - 0.5;
y = yy + s;
figure(2);plot(y,'b')
% 计算互相关序列
r = xcorr(x,y);
figure(3);plot(r)
n = length(r);
nn = (n - 1)/2;
figure(4);plot(-nn:nn,'r')
[maxR,id] = max(r)

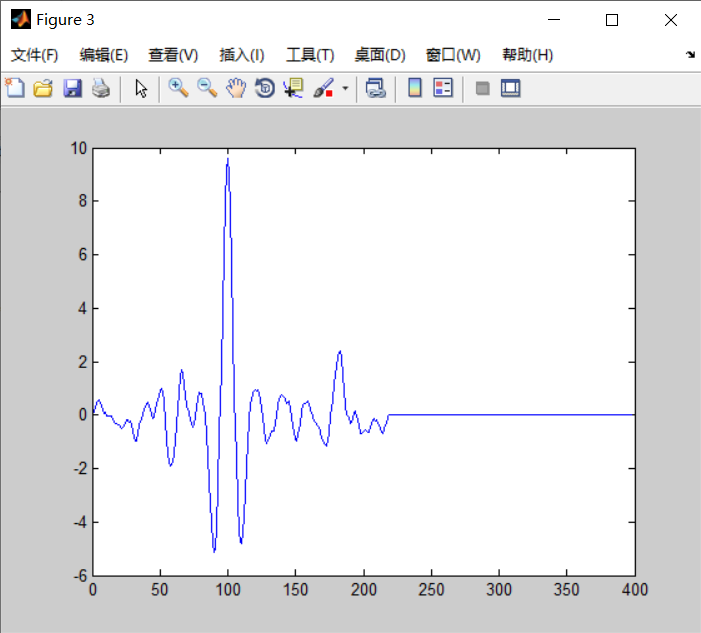
2.8.2.3 寻找被噪声淹没的周期信号的周期值

​ 利用自相关运算寻找被噪声淹没的周期信号的周期值。得到自相关运算的计算结果后，对比自相关序列与原始周期序列的周期是否相同。

N = 96;
n = 1:N;
x = cos(pi*0.25*n); 
d = rand(1,N) - 0.5; % 添加随机噪声
y = x + d; % 构建合成信号
r = xcorr(x,x); 
[peaks,locs] = findpeaks(r)  % 查找数据中的峰值及峰值所在位置
k = -28:28;
stem(k, r(68:124))
xlabel('时间序号n'); ylabel('振幅');

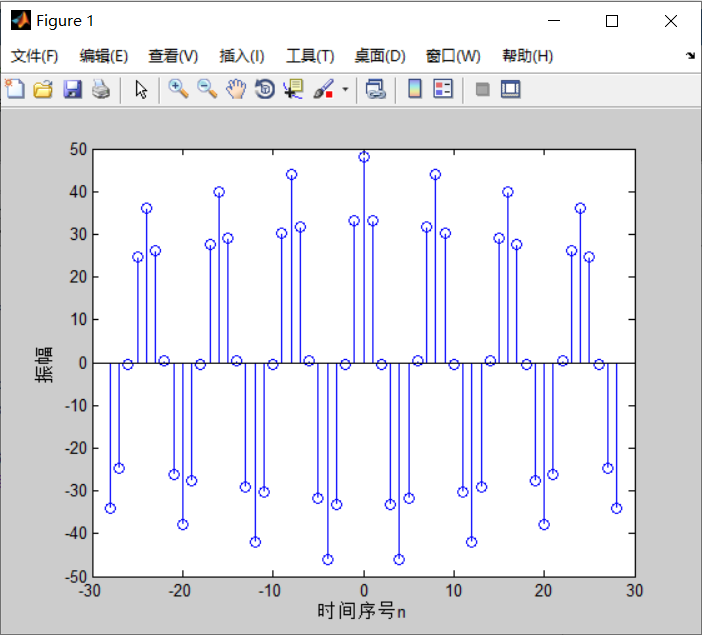
最后

以上就是俊秀枕头为你收集整理的【MATLAB数字信号处理】离散时间系统的时域分析（三）的全部内容，希望文章能够帮你解决【MATLAB数字信号处理】离散时间系统的时域分析（三）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。