线性时不变系统的定义
线性时不变系统(LTI)是离散时间系统中特别重要的一种系统,该系统包含线性以及时不变性,用卷积来表征。
前面有讲过序列$x[n]$可以表示成幅度加权的延迟单位样本序列的和的形式
$x[n] = displaystyle{ sum_{k=-infty}^{infty}x[k]delta[n-k] }$
因此离散时间系统可以表示成如下形式
$y[n] = Tleft{ displaystyle{ sum_{k=-infty}^{infty}x[k]delta[n-k] } right}$
如果系统是线性的,那么由于式子中的变量为$n$,根据叠加原理,$displaystyle{ sum_{k=-infty}^{infty}x[k] }$可以移出$T$
$y[n] = displaystyle{ sum_{k=-infty}^{infty}x[k]T{ delta[n-k] } }$
我们令$h_k[n] = T{delta[n-k]}$,$h_k[n]$就是该线性系统对输入为$delta[n-k]$所产生的输出,也就是系统对位于$n=k$处脉冲的响应,被称为脉冲响应(impulse response)。
如果系统是时不变的,这意味着如果$h[n]$是系统对$delta[n]$的响应,那么$h[n-k]$就是系统对$delta[n-k]$的响应,此时可以得到
$y[n] = displaystyle{ sum_{k=-infty}^{infty}x[k]h[n-k] }$
上面的式子表明,对于一个线性时不变系统,如果我们知道其的全部输入$x[n]$以及该系统的脉冲响应$h[n]$,则能得到其全部输出$y[n]$。该式子一般被称为卷积和(convolution sum),并用下述操作符号表示
$y[n] = x[n]*h[n]$
※单位脉冲响应$h[n]$的定义就是当单位脉冲$delta[n]$经过LTI系统时所产生的输出。
LTI系统的两种解释/计算方式
如上一小节所述,线性时不变系统对应的算式为
$y[n] = displaystyle{ sum_{k=-infty}^{infty}x[k]h[n-k] }$
单独分析每一个输入脉冲
LTI系统可以理解为:对于序列$x[n]$中的某一项脉冲$x[k_0]$,其在经过LTI系统后得到的脉冲响应为$x[k_0]h[n-k_0]$,把序列$x[n]$的所有脉冲的脉冲响应线性相加就得到最终输出$y[n]$。
假设有一个LTI系统,其输入序列$x[n]$、系统脉冲响应$h[n]$如下
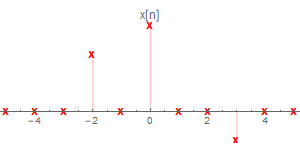
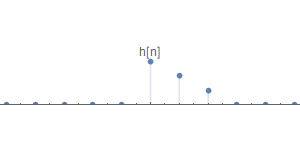
可以看到$x[n]$有三个脉冲$x_{-2}[n],x_{0}[n],x_{3}[n]$,我们把这三个脉冲单独取出来,分别计算它们经过LTI系统后的的脉冲响应。
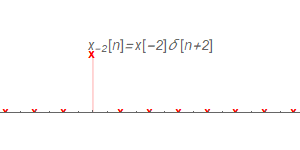
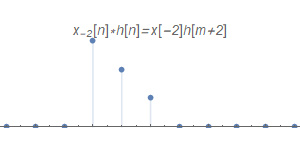
把$x_{-2}[n]$看作加权$x[-2]$与$delta[n+2]$的乘积,按照LTI系统的时不变性质,$delta[n+2]$的脉冲响应就是$h[n+2]$;又因为LTI系统的线性性质,可以得到$x_{-2}[n]$的脉冲响应为$x[-2]h[n+2]$。同理,剩下的脉冲响应如下
$x_{0}[n]$
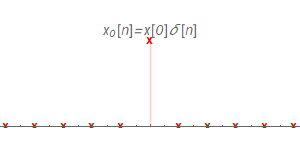
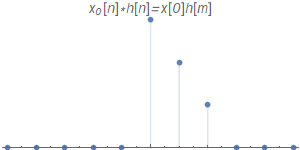
$x_{3}[n]$
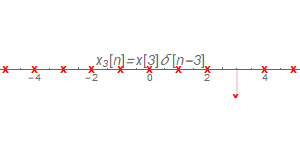
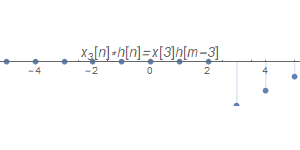
最后由于LTI系统具有线性性质,因此把所有的脉冲响应结果线性相加,即可得到$x[n]$经过系统后的输出$y[n]$
![x[n] x[n]](https://www.shuijiaxian.com/files_image/20230520/202305200051317631807.png)
![y[n] y[n]](https://www.shuijiaxian.com/files_image/20230520/202305200051314929117.png)
单独分析每一个输出脉冲
$y[n]$是系统的输出序列,对于某一时间点$n_0$的输出脉冲$y[n_0]$,我们可以通过卷积分析该输出脉冲如何通过计算得到,按照这种计算方法对所有时间点的输出脉冲进行计算,就能得到整个输出序列$y[n]$。
我们首先取某时间点$n_0$,其输出脉冲为
$y[n_0] = displaystyle{ sum_{k=-infty}^{infty}x[k]h[n_0-k] }$
此时,式子当中的$n_0$为常量,$k$为变量,我们接下来观察$h[n_0-k]$是通过$h[k]$做何种变化得到的。
- 令$h_1[k]=h[-k]$,即$h[k]$对$k=0$轴进行对称反转即可得到$h_1[k]$
- 令$h_2[k]=h_1[k-n_0]$,即$h_1[k]$向右移动$n_0$个单位即可得到$h_2[k]$
$h_2[k] = h_1[k-n_0]=h[-(k-n_0)]=h[n_0-k]$
在知道输入$x[k]$的情况下,现在我们又得到了$h[n_0-k]$,如此一来就能通过上述式子的乘积求和计算得到$y[n_0]$。通过改变$n_0$,就能得到输出序列$y[n]$。
假设有一LTI系统的脉冲响应$h[n]$及其输入$x[n]$如下
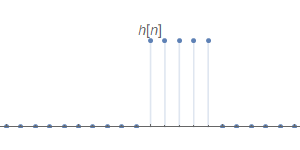
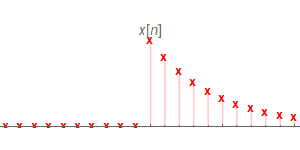
当$n_0<0$的时候,$h[n_0-k]$与$x[k]$并没有相交,因此$y[n_0]=0$
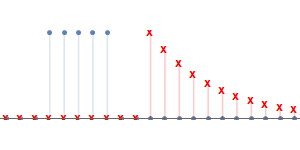
从$n_0=0$开始,$h[n_0-k]$与$x[k]$部分相交,直到$n_0=4$开始完全相交,因此在这段时间内计算得到的$y[n_0]$呈上升趋势
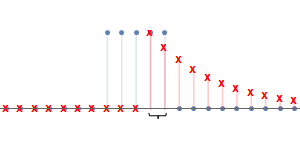
在$n_0=4$时有最大值$y[4]$,然后$y[n_0]$呈下降趋势
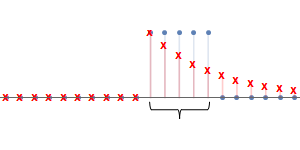
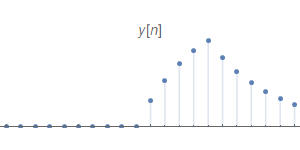
最终得到的$y[n]$如下
线性时不变系统的性质
交换律、分配律、结合律
LTI系统由离散时间卷积来定义,而卷积满足交换律、分配律、结合律。
交换律推导:
$begin{align*}
y[n] &=x[n]*h[n] \
&=sum_{m=-infty}^{infty}x[n-m]h[m] \
&=sum_{p=-infty}^{infty}x[p]h[n-p] quad letting p=n-m \
&=sum_{p=-infty}^{infty}h[n-p]x[p] \
&=h[n]*x[n]
end{align*}$
分配律推导:
$begin{align*}
y[n] &=x[n]*h[n] \
&=x[n]*(h_1[n]+h_2[n]) \
&=sum_{m=-infty}^{infty}x[n-m](h_1[m]+h_2[m]) \
&=sum_{m=-infty}^{infty}x[n-m]h_1[m]+sum_{m=-infty}^{infty}x[n-m]h_2[m] \
&=x[n]*h_1[n]+x[n]*h_2[n]
end{align*}$
结合律推导:
$begin{align*}
y[n] &=(x[n]*h_1[n])*h_2[n] \
&=z[n]*h_2[n] \
&=sum_{m=-infty}^{infty}z[n-m]h_2[m] \
&=sum_{p=-infty}^{infty}z[p]h_2[n-p] quad letting p=n-m\
&=sum_{p=-infty}^{infty}left ( sum_{i=-infty}^{infty}x[p-i]h_1[i] right )h_2[n-p] \
&=sum_{p=-infty}^{infty}left ( sum_{q=-infty}^{infty}x[q]h_1[p-q] right )h_2[n-p] quad letting q=p-i\
&=sum_{q=-infty}^{infty}x[q]left ( sum_{p=-infty}^{infty}h_1[p-q]h_2[n-p] right ) \
&=sum_{q=-infty}^{infty}x[q]left ( sum_{m=-infty}^{infty}h_1[n-q-m]h_2[m] right ) \
&=sum_{k=-infty}^{infty}x[n-k]left ( sum_{m=-infty}^{infty}h_1[k-m]h_2[m] right ) quad letting k=n-q \
&=x[n]*(h_1[n]*h_2[n])
end{align*}$
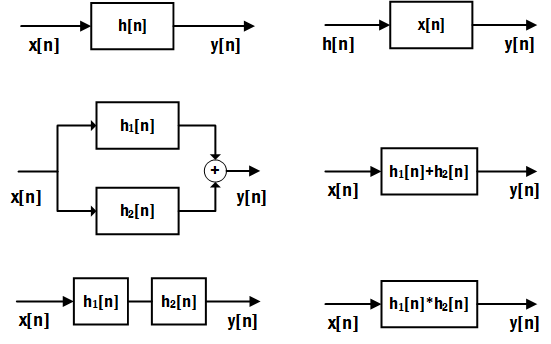
因此LTI系统有如下性质:
- 一个LTI系统在输入为$x[n]$和单位脉冲响应为$h[n]$,与输入为$h[n]$和单位脉冲响应为$x[n]$将得到相同的输出。
- 一个LTI系统如果由并联的两个部分组成,其单位脉冲响应分别为$h_1[n],h_2[n]$,那么整个系统的单位脉冲响应等价于$h[n]=h_1[n]+h_2[n]$。
- 一个LTI系统如果由级联的两个部分组成,其单位脉冲响应分别为$h_1[n],h_2[n]$,那么整个系统的单位脉冲响应等价于$h[n]=h_1[n]*h_2[n]$。
稳定性
认为一个稳定系统就是对每个有界的输入均产生一个有界的输出。当单位脉冲响应是绝对可加时,LTI系统才是稳定的,即
$B_h=displaystyle{ sum_{k=-infty}^{infty}|h[k]|<infty }$
证明:
$displaystyle{ |y[n]|=left | sum_{k=-infty}^{infty}h[k]x[n-k] right |leqslantsum_{k=-infty}^{infty}|h[k]||x[n-k]| }$
如果$x[n]$是有界的,则存在一个足够大的数$B_x$,使得
$|x[n]|leqslant B_x$
用$B_x$替换$|x[n-k]|$可以得到一个更大的数值,即
$|y[n]|leqslant B_xB_h$
因此,当单位脉冲响应是绝对可加时,LTI系统是稳定的。
因果性
因果系统就是其输出$y[n_0]$仅仅与$nleqslant n_0$时的输入样本$x[n]$有关的系统,如果一个LTI系统是因果系统,则该系统应满足
$h[n]=0, quad n<0$
证明:
设某时刻$n_1$的输出为$y[n_1]$,有
$begin{align*}
y[n_1] &= sum_{k=-infty}^{infty}x[k]h[n_1-k] \
&=sum_{k=-infty}^{n_1}x[k]h[n_1-k]+sum_{k=n_1+1}^{infty}x[k]h[n_1-k]
end{align*}$
因为是因果系统,即$y[n_1]$与输入序列$x[k]$的$k>n_1$部分无关,即
$displaystyle{ sum_{k=n_1+1}^{infty}x[k]h[n_1-k] =0}$
令$m=n_1-k,k=n_1-m$,代入上式,得到
$displaystyle{ sum_{m=-infty}^{-1}x[n_1-m]h[m]=0 }$
其中$x[m]$为可变的输入序列,要使上式成立,则需要
$h[m]=0,quad m<0$
级联系统的某些应用
LTI系统用卷积来表征,并且从前一小节我们得知级联系统由离散时间卷积来表征。两个序列之间的卷积运算会带来很多涉及系统问题的简化。
一个很常用的应用就是将一个移位样本序列与任何$x[n]$进行卷积,其结果只是将$x[n]$做相同的移位:
$x[n] * delta[n-n_d] = delta[n-n_d] * x[n] = x[n-n_d]$
这种移位的应用在LTI系统互联与分析中也常常用到,如一个前向差分与一个理想延迟(延迟一个样本)级联就能得到一个后向差分:
$begin{align*}
h[n] &=(delta[n+1]-delta[n])*delta[n-1] \
&=delta[n-1]*(delta[n+1]-delta[n]) \
&=delta[n]-delta[n-1]
end{align*}$
另外,级联系统引入了逆系统(inverse system)的概念,
$h[n] * h_i[n] = h_i[n] * h[n] = delta[n]$
如果两个系统级联后得到的是$delta[n]$,则这两个系统互为逆系统。
转载于:https://www.cnblogs.com/TaigaCon/p/8058634.html
最后
以上就是开放期待最近收集整理的关于[离散时间信号处理学习笔记] 2. 线性时不变系统线性时不变系统的定义LTI系统的两种解释/计算方式线性时不变系统的性质级联系统的某些应用的全部内容,更多相关[离散时间信号处理学习笔记]内容请搜索靠谱客的其他文章。




![[离散时间信号处理学习笔记] 2. 线性时不变系统线性时不变系统的定义LTI系统的两种解释/计算方式线性时不变系统的性质级联系统的某些应用](https://www.shuijiaxian.com/files_image/reation/bcimg13.png)



发表评论 取消回复