1.LSI系统的转移函数

对于一个线性时不变离散时间系统（如下图所示），我们在之前就已经接触到了4种不同的描述方法。

1.1 频率响应

$$H(e^{j\omega })=\sum _{n=0}^{\infty }h(n)e^{-j\omega n}$$

1.2 转移函数

$$H(z)=\sum _{n=0}^{\infty }h(n)z^{-n}$$

1.3 差分方程

$$y(n)=-\sum _{k=1}^{N}a(k)y(n-k)+\sum _{r=0}^{M}b(r)x(n-r)$$

1.4 卷积关系

$$y(n)=x(n)\ast h(n)=\sum _{k=-\infty }^{\infty }x(k)h(n-k)$$
上边的4种方法从不同的角度描述了一个LSI系统的物理特性，他们之间有着密切的联系，其联系的纽带就是系统的单位冲激响应$h(n)$

1.5 系统的转移函数$H(Z)$

对上边的第三式两边取Z变换，得
$$\begin{gathered} Y(z)=-Y(z)\sum _{k=1}^{N}a(k)z^{-k}+X(z)\sum _{r=0}^{M}b(r)z^{-r} \\ Y(z)[1+\sum _{k=1}^{N}a(k)z^{-k}]=X(z)[b(0)+\sum _{r=1}^{M}b(r)z^{-r}] \end{gathered}$$
对上边的式子进行整理可得
$$H(z)=\frac{Y(z)}{X(z)}=\frac{{\sum }_{r=0}^{M}b(r)z^{-r}}{1+{\sum }_{k=1}^{N}a(k)z^{-k}}$$
上式$H(z)$就被称为系统的转移函数。它即可以定义为系统单位抽样响应$h(n)$的z变换，也可以 定义为系统的输出、输入Z变换之比。

2.matlab编程训练，求系统的阶跃响应

我们之前学过的，如果已经知道系统的$h(n)$,由于$y(n)=x(n)\ast h(n)$,则我们可以轻松的使用conv函数将其求得，但是如果我们不知道$h(n)$,已知$Y(z)$、$X(z)$,需要求$y(n)$，则我们可以根据公式，
$$\begin{gathered} y(n)=-\sum _{k=1}^{N}a(k)y(n-k)+\sum _{r=0}^{M}b(r)x(n-r) \\ =b(1)x(n)+b(2)x(n-1)+...+b(n_b+1)x(n-n_b) \\ -a(2)y(n-1)-...-a(n_a+1)y(n-n_a) \end{gathered}$$
求取我们的$y(n)$,使用matlab内的一个函数$y=filter(b,a,x)$其中$x、y、a和b$都是向量。

2.1 编程实训

已知一个系统的转移函数如下所示：
$$H(z)=\frac{0.001836+0.007344z^{-1}+0.011016z^{-2}+0.007374z^{-3}+0.001836z^{-4}}{1-3.0544z^{-1}+3.8291z^{-2}-2.2925z^{-3}+0.55075z^{-4}}$$
求该系统的阶跃响应。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
%%转移函数
clc;
clear;
x=ones(100,1);
%定义阶跃输入
t=1:100;
b=[0.001836,0.007344,0.011016,0.007374,0.001836];
%定义向量b
a=[1,-3.0544,3.8291,-2.2925,0.55075];
%定义向量a
y=filter(b,a,x);
%得到y(n)
hold on
h1=plot(t,x,'b');
h2=plot(t,y,'r');
hold off
%画图结束
legend([h1,h2],'阶跃输入','阶跃响应');
%添加标注

其运行结果为：

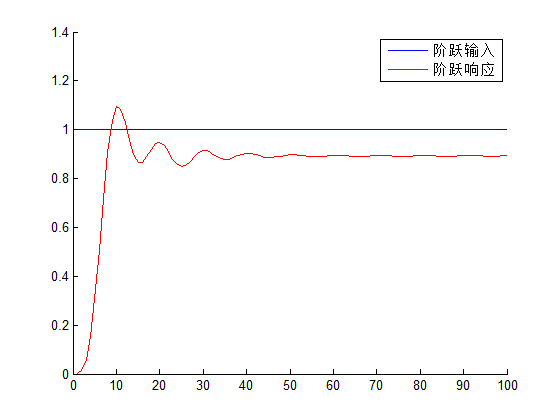
2.2 求取系统的单位抽样响应h(n)

在我们得到上边的情况下，如果我们想要得到该系统的单位抽样响应，编辑mtalab代码如下：

1
2
3
4
5
6
[h,t]=impz(b,a,40);
%令h(n)的长度为N=40
stem(t,h,'.');
%绘制离散的h(n)
grid on;

其显示结果如下所示：

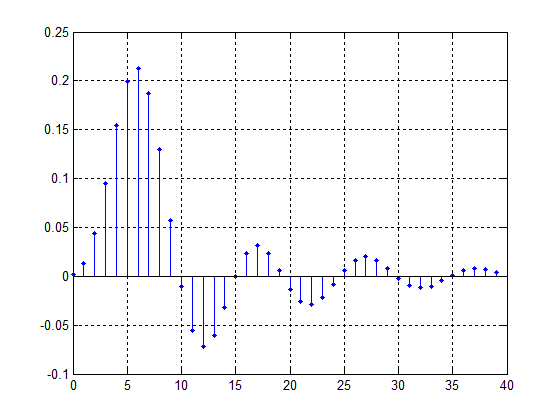
2.3 求上述系统的频率响应

1
2
3
4
5
6
7
8
9
10
11
12
13
14
%%得到系统的频率响应
[H,w]=freqz(b,a,256,'whole',1);
%whole 指定计算的频率范围是0-Fs,此处我们设置Fs=1
Hr=abs(H);
%得到绝对值，也就是幅度值
plot(w,Hr,'r','linewidth',2);
%绘制图形，并且设置颜色和线宽
grid on;
%显示方格
xlabel('omega /2pi');
ylabel('|H(e^{jomega})|');
title('幅频响应')
%坐标轴设置

输出图像如下所示：

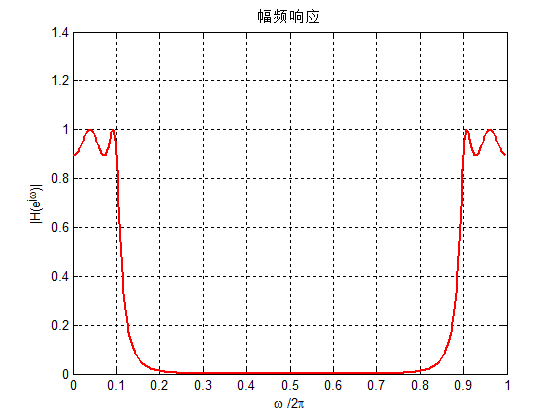
3.参考文章

数字信号处理理论、算法与实现（第三版）

最后

以上就是老迟到钻石最近收集整理的关于数字信号处理matlab训练第【3】弹--求取离散系统的输出1.LSI系统的转移函数2.matlab编程训练，求系统的阶跃响应3.参考文章的全部内容，更多相关数字信号处理matlab训练第【3】弹--求取离散系统内容请搜索靠谱客的其他文章。