matlab编写关于离散时间信号的基础运算

96 阅读 0 评论 64 点赞

我是靠谱客的博主暴躁指甲油，最近开发中收集的这篇文章主要介绍matlab编写关于离散时间信号的基础运算，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

1.离散时间系统

离散时间系统是将输人序列x(n)(通常称做激励)变换成输出序列y(n)(通常称做响应)的一种运算,变换过程用T[ ]描述。因此,一个离散时间系统可以表示为y(n) = T[x(n)]

离散时间系统还可分成线性和非线性两种。同时具有叠加性和齐次性(均匀性)的系统,通常称为线性离散系统。当若干个输入信号同时作用于系统时，总的输出信号等于各个输人信号单独作用时所产生的输出信号之和,这个性质称为叠加性。

线性系统(linear system):满足叠加原理的系统。

线性系统用数学语言描述如下:
若序列y1(n)和y2(n)分别是输入序列x1(n)和x2(n)的输出响应,即
y1(n)= T[x1(n)]，y2(n) = T[x2(n)]，如果系统T[ ]是线性系统,那么下列关系式一定成立:
T[x1(n) +x2(n)]= T[x(n)]+ T[x2(n)]= y1(n)+ y2(n)

注意这里不是重复，而是反应系统的叠加性，即单独输入对应单独的响应
T[ax1(n)]= aT[x1(n)]= ay1(n)

式中,a是任意常数。满足上面第一个式子的称系统具有叠加性( SuperpositionProperty),满足后面式子称系统具有比例性或齐次性(Homogeneity)。将两式结合起来表示为
T[ax1(n) + bx2(n)]= aT[x1(n)] + bT[x2(n)]= ay1(n) + by2(n)

式中,a和b均为任意常数。如果系统的输出响应随输人的移位而移位,即若y(n) = T[x(n)]，y(n-k) = T[x(n-k)]，那么称这样的系统为时不变系统(Time-InvariantSystem)。式中,k为任意整数。

描述一个线性时不变离散时间系统,有如下两种常用方法:
(1)用单位冲激响应来表征系统;
(2)用差分方程(Difference Equation)来描述系统输人和输出之间的关系。

2.离散时间系统响应

在MATLAB中,函数filter 可以用来对差分方程在指定时间范围内的输人序列所产生的响应进行求解,该丽数的调用方法如下:
y= filter(b,a,x)，
其中,x为输人的离散序列,y为输出的离散序列,y的长度与x的长度一样,b与a分别为差分方程右端与左端的系数向量。

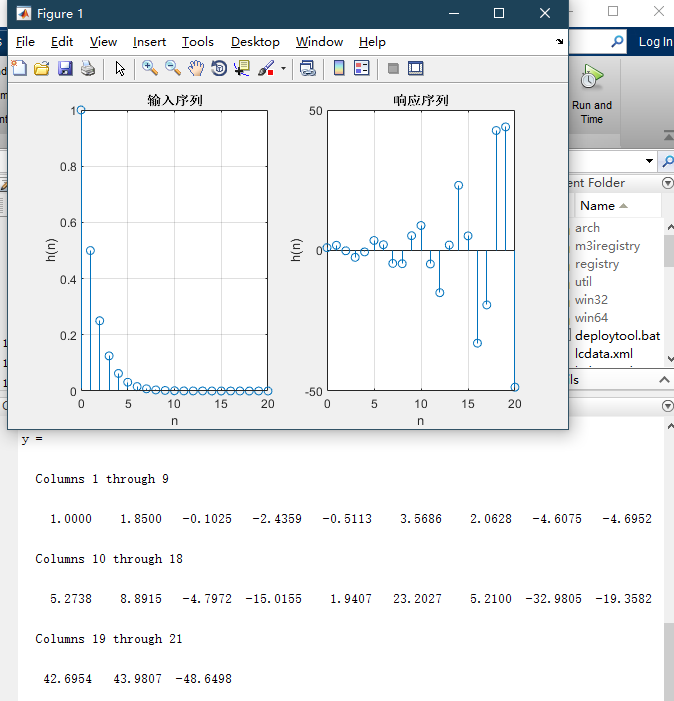
例1 已知 y(k) - 0.35y(k- 1)+1.5y(k- 2)= f(k)+ f(k-1),f(k)=(1/2)^k u(k),求零状态响应。

a=[1 -0.35 1.5];
b=[1 1];
t = 0:20;
x=(1/2).^t;
y = filter(b,a,x)
subplot(1,2,1)
stem(t,x)
title('输入序列')
grid on
xlabel('n'); ylabel( 'h(n)');
subplot(1,2,2)
stem(t,y)
xlabel('n'); ylabel( 'h(n)');
title('响应序列')
grid on

在这里插入图片描述

3.离散时间系统的冲激响应和阶跃响应

在MATLAB中,函数impz用于求解离散时间系统单位冲激响应,其调用形式为
h= impz(b,a, k)
式中,a、b分别是差分方程左、右端的系数向量,k表示输出序列的取值范围(可省),h就是系统单位冲激响应(如果没有输出参数,直接调用impz(b, a, k),则MATLAB将会在当前绘图窗口中自动画出系统单位冲激响应的图形)。

注意这里阶跃响应就是δ(n)=u(n)-u(n-1):所以阶跃响应也可以表示出来

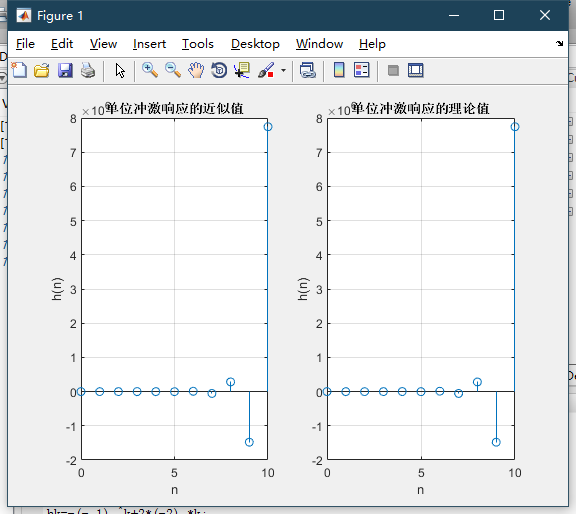
例2 用impz函数求下列离散时间系统的单位冲激响应。

k = 0:10;
a=[1 6 4];
b=[1 3];
h= impz(b, a,k);
subplot(1,2, 1);stem(k, h);
xlabel('n'); ylabel( 'h(n)');
title('单位冲激响应的近似值');
grid on;
hk=-(- 1).^k+2*(-2).*k;
subplot(1,2,2);stem(k, h);
xlabel('n'); ylabel( 'h(n)');
title('单位冲激响应的理论值');
grid on;

在这里插入图片描述

4.离散时间信号的卷积和运算

卷积是用来计算系统零状态响应的有力工具,由于系统的零状态响应是激励与系统
的单位取样响应的卷积,因此卷积运算在离散时间信号处理领域被广泛应用。离散时间
信号的卷积定义为
y(n) = x(n)*h(n)= Σx(m)h(n- m)，m取值从负无穷到正无穷

在MATLAB中,conv函数用于计算两个离散序列卷积和的函数,其调用形式为c= conv(a, b)
式中,a、b分别为待卷积的两序列的向量表示,c是卷积结果。向量c的长度为向量a、b
的长度之和减1,即length©= length(a) + length(b)-1。

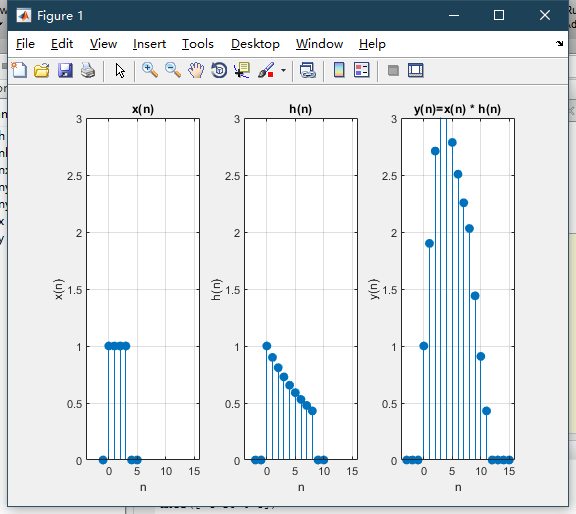
例3 已知某系统的单位样值响应为h(n)=0.9^n [u(n)- u(n- 9)],试用MATLAB求当激励信号为x(n)=u(n)- u(n- 4)时，系统的零状态响应。(求卷积)

function y= uDT(n)

y = n>=0;

clear
nx= -1:5;
nh= -2:10;
x= uDT(nx) - uDT(nx-4);
h=0.9.^nh.* (uDT(nh)-uDT(nh- 9));
y= conv(x, h);
ny1= nx(1) + nh(1);
ny= ny1 + (0:(length(nx) + length(nh) - 2));
subplot(131)
stem(nx,x, 'fill'),grid on
xlabel('n'), ylabel( 'x(n)');
title( 'x(n)')
axis([ -4 16 0 3])
subplot(132)
stem(nh, h', 'fill'),grid on
xlabel( 'n');ylabel( 'h(n)');
title( 'h(n)')
axis([-4 16 0 3])
subplot(133)
stem(ny,y, 'fill'),grid on
xlabel('n');ylabel('y(n)');
title('y(n)=x(n) * h(n)')
axis([-4 16 0 3])