离散数学（下）第九章 代数系统

1.n元运算概念的定义

要点：运算封闭（运算结果还在集合当中）
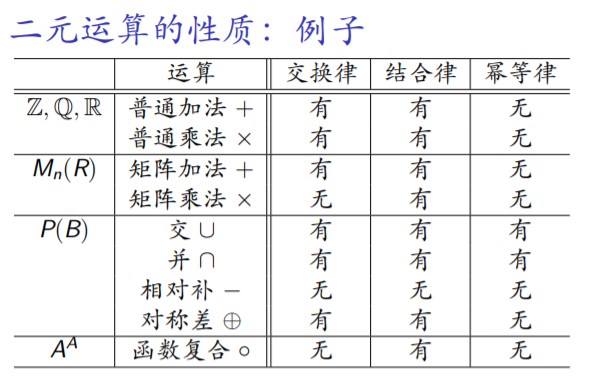
2.二元运算的性质：例子


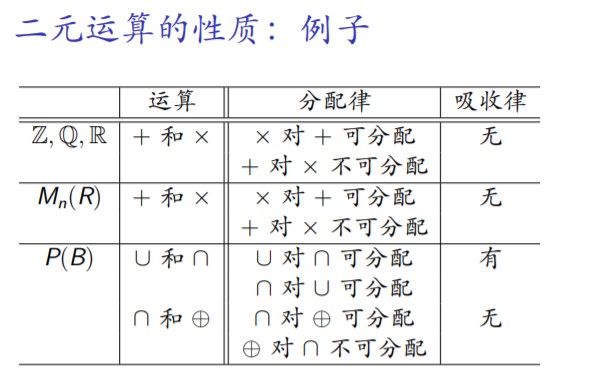
3.二元运算的吸收律和消去律
吸收律：

消去律：

要点：消去的不能是运算的零元（因为无论左右两边的数相不相同，乘上零元都能使左右两边相等）
4.代数系统的概念、组成要素以及表示


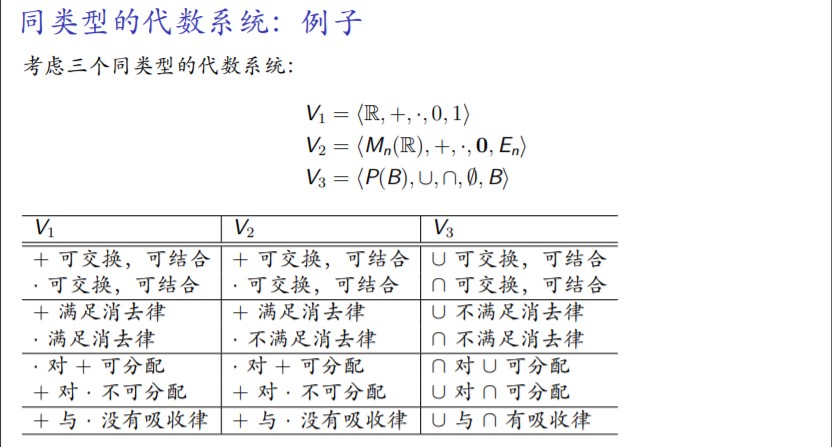
5.同类型的系统代数的概念以及例子


6.子代数的概念

要点：对所有运算封闭，其次看是否含相同的代数常数
7.子代数相关概念以及例子
对于代数系统 V = ⟨S, f1, f2, . . . , fk⟩
（1）子代数总是存在
（2）最大子代数：V本身
（3）最小子代数：如果 V 中所有的代数常数构成的集合 B 对所有的运算是封闭的，则 B 构成了
V 的最小子代数
（4）最大子代数与最小子代数统称为平凡子代数
（5）若 B 是 S 的真子集，则 B 构成的子代数称为 V 的真子代数

8.积代数的定义

要点：这里的a1,a2以及b1,b2仍然按原来的运算（比如取模加法、取模减法等等）
9.积代数的性质
除不保留构成它的代数的消去律外，其他如交换律、代数常数（结合得到新的代数常数）等都得到保留
理由：如果其中有取模加法，在保证消去的为非零元的基础上，如果另一个都是加上模的不同倍数也能使结果相等
10.代数系统的同态和同构的定义（单个或多个运算）


要点：同态性质可以理解为括号内的x与y的二元运算再函数结果可以等价于x的函数结果与y的函数结果再二元运算

最后

以上就是感性乐曲为你收集整理的离散数学（下）第九章 代数系统的全部内容，希望文章能够帮你解决离散数学（下）第九章 代数系统所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。