matlab输入pid算法,深刻浅出PID控制算法（二）————PID算法离散化和增量式PID算法原理及Matlab实现...

引言

上篇介绍了连续系统的PID算法，可是计算机控制是一种采样控制，他只能根据采样时刻的误差来计算控制量，所以计算机控制系统中，必须对公式进行离散化，具体就是用求和代替积分，用向后差分来代替微分，使模拟PID离散化为数字形式的差分方程。web

准备工做

在采样周期足够小时，能够做以下近似：

式中算法

T————为采样周期

k————为采样序号，k=0,1,2….

用这种近似方法，能够获得两种形式数字PID控制算法编程

位置式PID算法

由前面推倒很容易获得离散化后的表达式

由此式能够看出数字调节的输出u(k)跟过去的全部误差信号有关，计算机须要对e(i)进行累加，运算量太大，通常不用，重点说明增量式PID算法。svg

增量式PID算法

因为增量式PID的算法不够方便，不只对误差进行累加，占用过多的存储单元，并且不方便写程序，因此须要进行一些改进，对位置式取增量，方法以下：

函数

Matlab仿真

分析过程

一、对G(s)进行离散化即进行Z变换获得Z传递函数G(Z)；

二、分子分母除以z的最高次数即除以z的最高次获得；

三、由z的位移定理Z[e(t-kt)]=z^k*E(z)逆变换获得差分方程；

四、PID编程实现

具体实现细节在代码注释中已经给出性能

%设一被控对象G(s)=50/(0.125s^2+7s),

%用增量式PID控制算法编写仿真程序

%(输入分别为单位阶跃、正弦信号，采样时间为1ms，控制器输出限幅：[-3,3],

% 仿真曲线包括系统输出及偏差曲线)。

ts=0.001; %采样时间

sys=tf(50,[0.125,7, 0]); %tf是传递函数 即被控对象函数G();

dsys=c2d(sys,ts,'z'); %把控制函数离散化取Z变换n阶定常离散系统差分方程

%在零初始条件下取Z变换：

%dsys即Y(z)/U(z)

[num,den]=tfdata(dsys,'v');% 离散化后提取分子、分母

u_1=0.0;

u_2=0.0;

y_1=0.0;

y_2=0.0;

x=[0,0,0]';

error_1=0;

error_2=0;

%核心代码

for k=1:1:1000

time(k)=k*ts; %采样次数

S=1;

if S==1 %阶跃输入

kp=6.5;ki=0.1;kd=1; %初始化PID

rin(k)=1; %Step Signal

elseif S==2 %正弦输入

kp=10;ki=0.1;kd=15;

rin(k)=0.5*sin(2*pi*k*ts); %Sine Signal 即实际输入

end

du(k)=kp*x(1)+kd*x(2)+ki*x(3); %PID Controller 控制系数

u(k)=u_1+du(k); %真正的PID输出应该为du+前一时刻的输出

if u(k)>=3

u(k)=3;

end

if u(k)<=-3

u(k)=-3;

end

%Linear model 难点就是把传递函数转化为差分方程，以实现PID控制。

yout(k)=-den(2)*y_1-den(3)*y_2+num(2)*u_1+num(3)*u_2; %实际输出 num为dsys分子多项式系数，den为dsys分母多项式系数，从n阶定常离散系统差分方程变化来的。

error(k)=rin(k)-yout(k); % 偏差 输入-输出

u_2=u_1; %保存上上次输入 为下次计算

u_1=u(k); %保存上一次控制系数 为下次计算

y_2=y_1; %保存上上次次输出 为下次计算

y_1=yout(k); %保存上一次输出 为下次计算

x(1)=error(k)-error_1; %KP的系数

x(2)=error(k)-2*error_1+error_2; %KD的系数

x(3)=error(k); %KI的系数

error_2=error_1; %上次的变上上次偏差

error_1=error(k); %此次的变上次的偏差

end

figure(1);

plot(time,rin,'b',time,yout,'r'); %输入 和实际控制输出

xlabel('time(s)'),ylabel('rin,yout');

figure(2);

plot(time,error,'r') %时间偏差输出曲线

xlabel('time(s)');ylabel('error');

仿真效果(PID调参后)

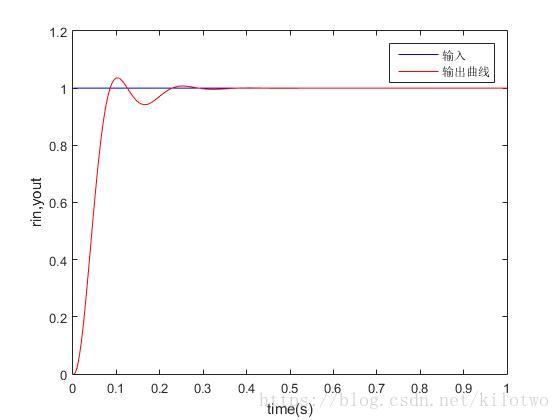
调参过程

(1)

肯定比例系数Kp

肯定比例系数Kp时，首先去掉PID的积分项和微分项，能够令Ti=0、Td=0，使之成为

纯比例调节。输入设定为系统容许输出最大值的60％～70％，比例系数Kp由0开始逐渐增大，直至系统出现振荡；再反过来，今后时的比例系数Kp逐渐减少，直至系统振荡消失。记录此时的比例系数Kp，设定PID的比例系数Kp为当前值的60％～70％。

(2)

肯定积分时间常数Ti

比例系数Kp肯定以后，设定一个较大的积分时间常数Ti，而后逐渐减少Ti，直至系统出现振荡，而后再反过来，逐渐增大Ti，直至系统振荡消失。记录此时的Ti，设定PID的积分时间常数Ti为当前值的150％～180％。

(3)

肯定微分时间常数Td

微分时间常数Td通常不用设定，为0便可，此时PID调节转换为PI调节。若是须要设定，则与肯定Kp的方法相同，取不振荡时其值的30％。

(4)

系统空载、带载联调

对PID参数进行微调，直到知足性能要求。ui

Simulink仿真部分

这里使用Simulink仿真也很是的方便，只须要设定好PID控制器的参数和传递函数便可

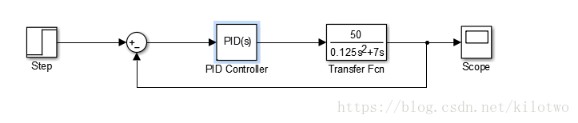
这里注意Filter coefficient这个参数起前向滤波做用，这里取得1

spa

微分环节的缺点，就是偏差e变化微弱的时候，若是D过大会产生过大的修正量，致使震动不但不减少反而扩大。

滤波器的做用就是滤除高频修正，使D更好用，说白了是一个改进型.net

运行后双击示波器查看结果

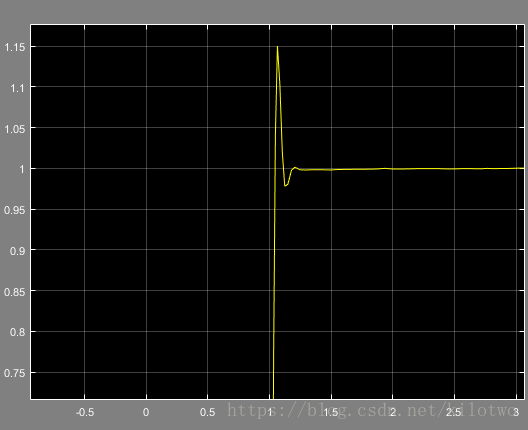调试

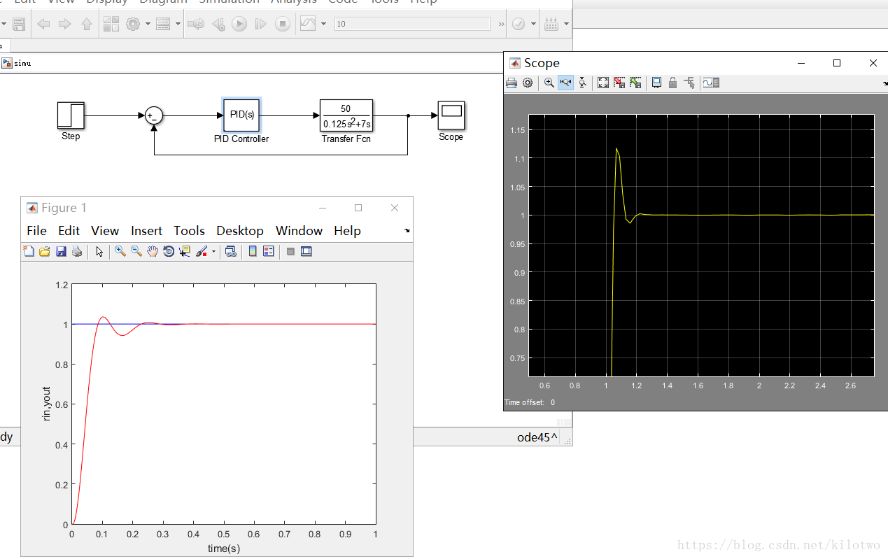
结论

(1)对于PID 参数采用 MATLAB 进行整定和仿真，使用起来不只快捷、方便，并且更为直观，同时也避免了传统方法反复修改参数调试。

(2)系统的响应速度会随Kp值的增大而加快，同时也有助于静差的减少，而Kp值过大则会使系统有较大超调，稳定性变坏；此外，系统的动做会由于太小的Kp值减慢。

(3)超调的减少、振荡变小以及系统稳定性的增长都取决于积分时间Ti的增大，可是系统静差消除时间会由于Ti的增大而变长。

(4)增大微分时间Td对于系统的稳定性、系统响应速度的加快以及系统超调量的减少都会有所帮助。可是若是Td过大，则会使得调节时间较长，超调量也会增大；若是Td太小，一样地也会发生以上情况。

(5)总之PID 参数的整定必须考虑在不一样时刻三个参数的做用以及彼此之间的做用关系。