离散数学12：代数系统

抽象代数的特点：

• 采用集合论的符号
• 重视运算及运算规律
• 使用抽象化和公理化的方法

以抽象的观点学习本章。

运算

二元运算

有序对代表着两个运算数（含顺序），其所映射到的单个元素就是运算结果。

一个运算是集合$S$上的二元运算应满足：

• 运算是封闭的：基于集合$S$上的运算，运算结果不能超出$S$的范围。
• $S$中任意两个元素均可以进行这种运算，且运算结果是唯一的。（函数定义的要求）

集合上所定义的二元运算的重要特性就是封闭性，这是与通常所说的运算的重要区别。

一元运算

运算表

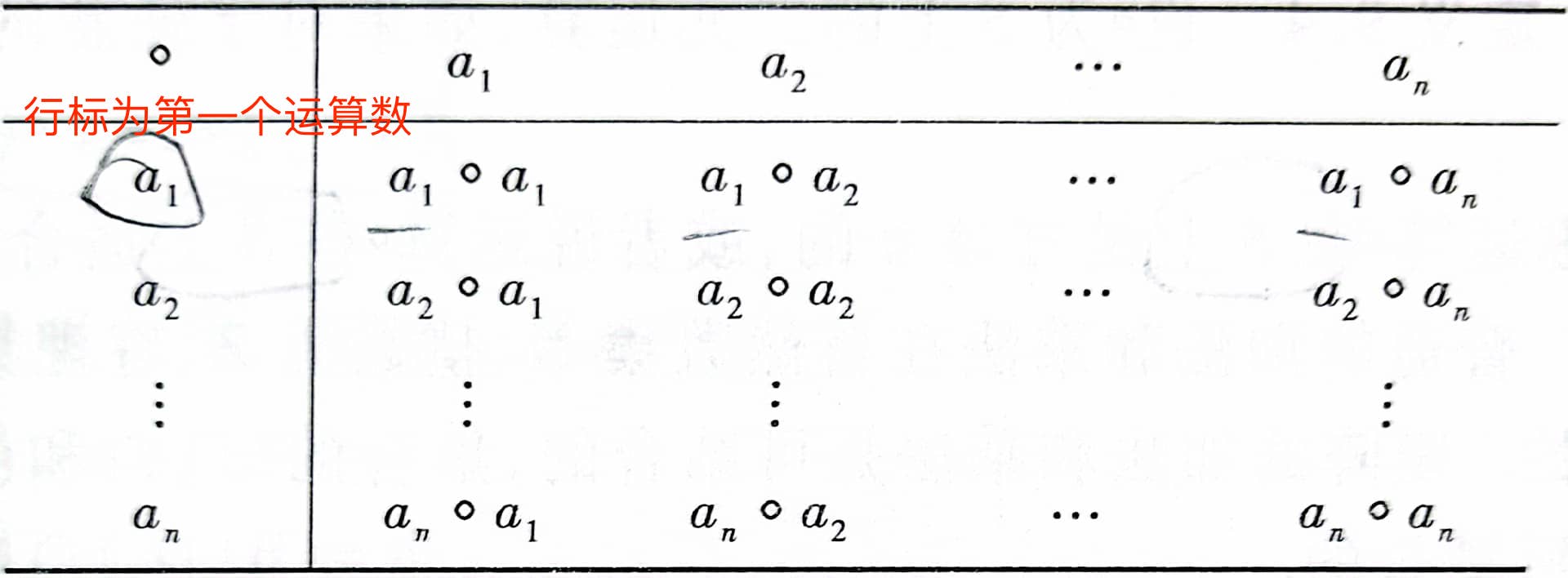
含有$n$个元素的集合上，可以定义$n^{n^2}$个运算，其中可交换的运算有$n^{\frac{n^2+n}{2}}$个，幂等的运算有$n^{n^2-n}$个，交换且幂等的运算有$n^{\frac{n^2-n}{2}}$个

运算律

设$\circ 、\ast$是集合$S$上的二元运算，

• 若$\forall x,y\in S$都有$x\circ y=y\circ x$，则称$\circ$运算在$S$上满足交换律
• 若$\forall x,y,z\in S$都有$(x\circ y)\circ z=x\circ (y\circ z)$，则称$\circ$运算在$S$上满足结合律
• 若$\forall x,y,z\in S$都有$x\ast (y\circ z)=(x\ast y)\circ (x\ast z)$ 且 $(y\circ z)\ast x=(y\ast x)\circ (z\ast x)$，则称 $\ast 对\circ$ 运算在$S$上满足分配律
• 在$\ast 对\circ$、$\circ 对\ast$均满足分配律的基础上，
  若$\forall x,y\in S$都有$x\ast (x\circ y)=x且x\circ (x\ast y)=x$，则称$\ast 和\circ$运算在$S$上满足吸收律.
  （满足吸收律的两个二元运算地位是一样的。）
• 若$\forall x,y,z\in S,x\ne \theta$，都有$x\circ y=x\circ z\Rightarrow y=z且y\circ x=z\circ x\Rightarrow y=z$，则称$\circ$运算在$S$上满足消去律

• 在进行消去时，要先判断所消去的元素是否为零元，零元不可以随意消去，（可能需要分类讨论）。
• 结合律的主要功能：定义幂运算$a^n$
• 交换律的主要功能：使$(ab{)}^n=a^n{b}^n$成立

• $R$上的减法不满足交换律、结合律
• R ∗ = R − { 0 } R^*=R-{0} R∗=R−{0}上的除法运算不满足交换律、结合律
• 矩阵乘法可结合，但不可交换
• 幂集$P(S)$上的并, 交, 对称差运算是可交换, 可结合的
• $S^S$上的函数复合运算可结合, 一般不可交换

---

• 幂集$P(S)$上的对称差运算满足消去律

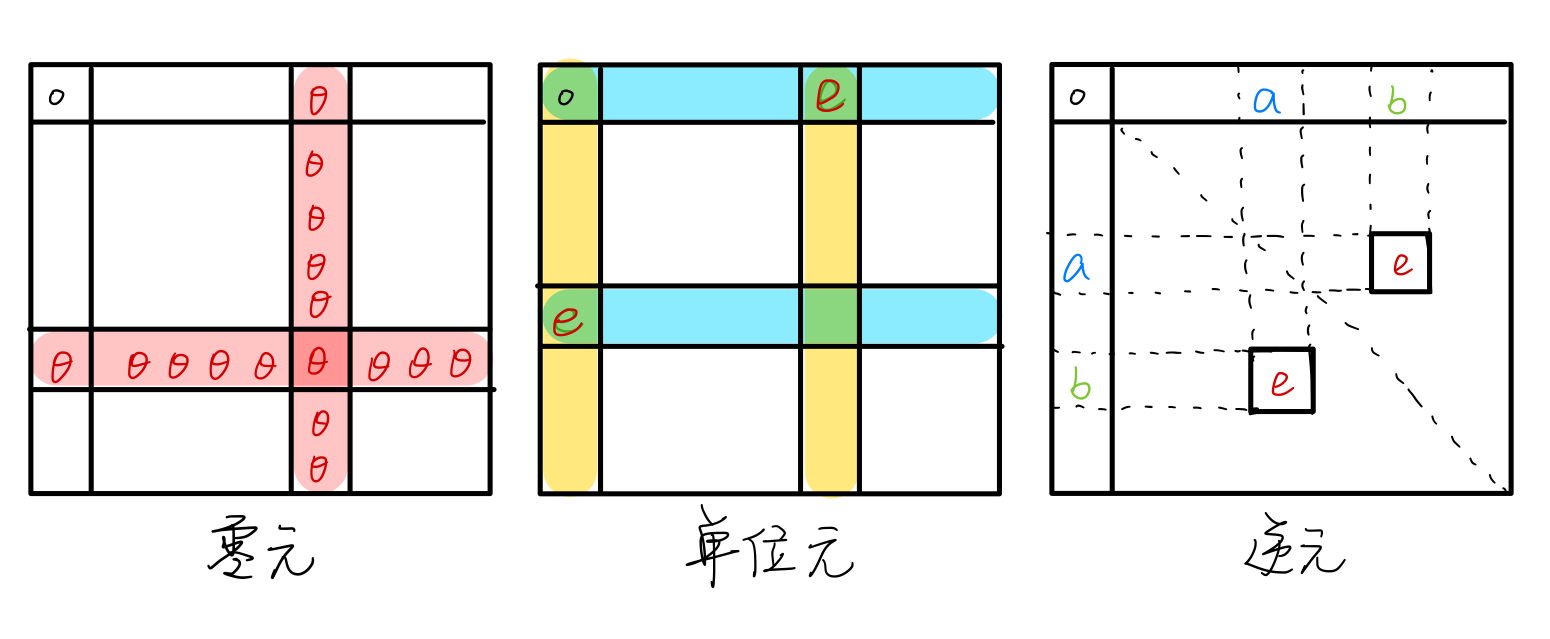
特殊元素

• 幂等元
  
  
  0是加法的幂等元，1是乘法的幂等元。

• 单位元
  
  $S$中关于◦运算的左单位元和右单位元若存在, 则它们相等且是惟一的，因此此时可直接用“单位元”来描述。

• 零元
  
  $S$中关于◦运算的左零元和右零元若存在, 则它们相等且是惟一的，因此此时可直接用“零元”来描述。

单位元是最“怂”的，零元是最“猛”的。
零元和单位元是代数系统中两个比较特殊的全局元素, 具有重要的地位.
在任一代数系统中, 可能存在零元和单位元, 但也可能不存在零元, 或不存在单位元，或都不存在.

实数集上，

• 关于加法的单位元是0, 没有零元;
• 关于乘法的单位元是1, 零元是0;
• 减法运算的右单位元是0, 无左单位元, 故无单位元.

幂集$P(S)$上，

• 关于∪运算的单位元是∅, 零元是$S$;
• 关于∩运算的单位元是$S$, 零元是∅.;
• ⊕运算的单位元是∅, 没有零元

若集合$S$中的元素个数多于1，则$S的零元\ne 单位元$。
若集合$S$中的元素个数 = 1，则其唯一的元素既是单位元，又是零元。

• 逆元
  
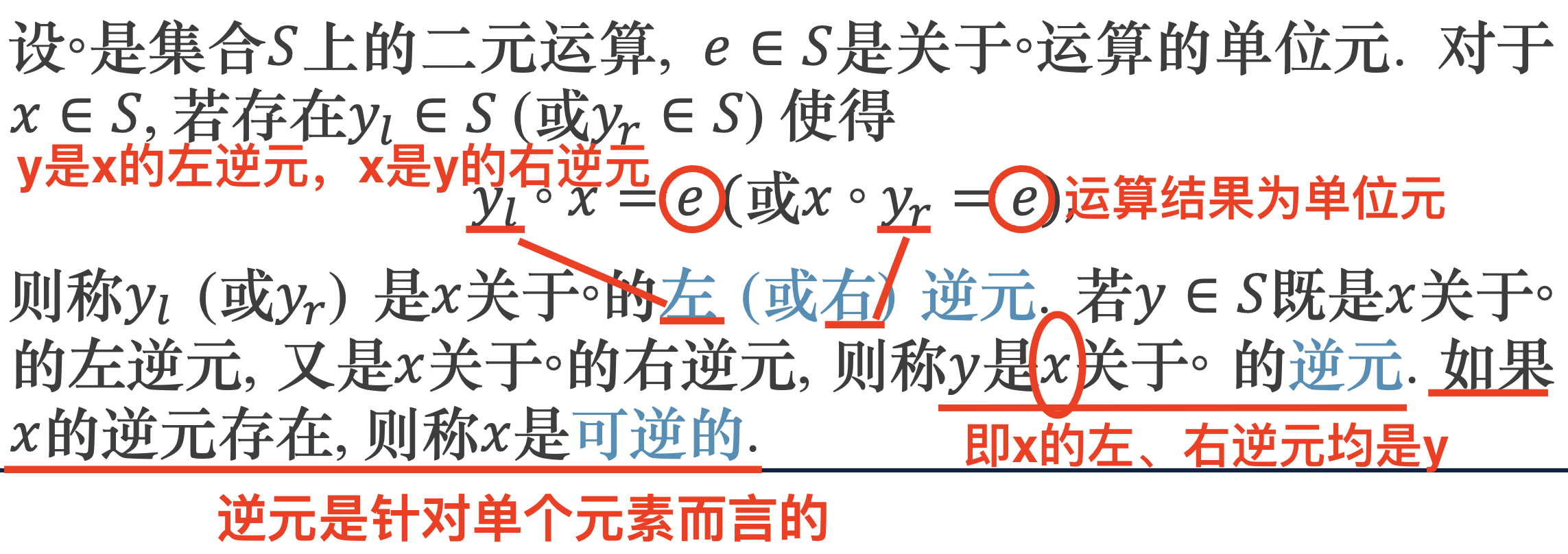
  求逆元，先得求出单位元。

对于任何二元运算, 单位元总是可逆的, 其逆元就是单位元自身。
若集合$S$的元素个数大于1，则零元是不可逆的；若$S$的元素个数为1，则逆元就是该元素本身（因为该元素就是单位元了）。

对于有单位元的代数系统而言, 任一元素可能不存在逆元, 也可能存在逆元, 甚至存在多个逆元 (不满足结合律)。
若$S$中某元素存在逆元，该运算满足结合律 $⟹$ 该逆元是唯一的。(注意：结合律成立是逆元惟一 的充分但不必要的条件)

$y_l=y_l\circ e=y_l\circ (x\circ y_r)=(y_l\circ x)\circ y_r=e\circ y_r=y_r$

代数系统

集合+集合上的运算（+特殊元素）$⟹$ 代数系统.
运算是代数系统的决定性因素。

可见，子代数（系统）与原代数系统的差别主要在于集合的不同。

积代数的性质：

虽然积代数$V_1\times V_2$,与因子代数$V_1$和$V_2$在许多性质上是共同的,有一种“继承”的感觉， 但并非因子代数的所有性质都在积代数中成立. 例如：因子代数满足消去律而在积代数中就不一定成立。

同态与同构

该定理说明：与代数系统$V_1$相联系的一些重要公理，在$V_1$的任何同态像中能够被保持下来。但$V_2$具有的性质未必在$V_1$中成立。
当$\phi$不是满同态时, 上述结论仅在$V_1$的同态像中成立，而不一定在$V_2$中成立。

深入理解同态与同构

最后

以上就是正直饼干为你收集整理的离散数学12：代数系统的全部内容，希望文章能够帮你解决离散数学12：代数系统所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。