离散数学-9 代数系统

410 阅读 0 评论 271 点赞

我是靠谱客的博主美丽万宝路，这篇文章主要介绍离散数学-9 代数系统，现在分享给大家，希望可以做个参考。

定义7.11 设_º为S上的二元运算, 如果对于任意的x,y,z∈S,满足以下条件：
（1）若x _ºy=x _ºz 且x≠θ，则y=z;
（2）若y _ºx=z _ºx 且x≠θ，则y=z;
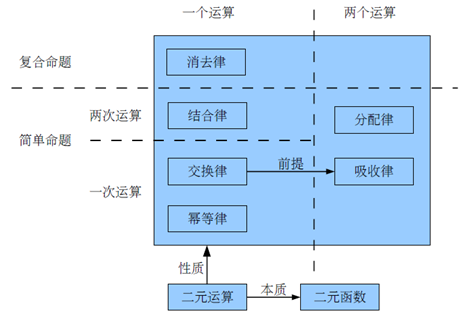
则称运算 _º满足消去律，（1）称作左消去律，（2）称作右消去律。
如果S中某些x满足x _ºx=x, 则称x为运算_º的幂等元

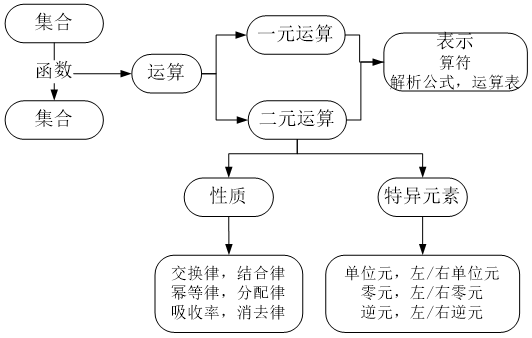
定义9.1 设S为集合，函数f：SSS 称为S上的二元运算，简

称为二元运算．

S中任何两个元素都可以进行运算，且运算的结果惟一．
S中任何两个元素的运算结果都属于S，即S对该运算封闭．
定义9.2 设S为集合，函数 f:S→S 称为S上的一元运算，简
称一元运算.
1．算符
可以用◦, ∗, · , , ,等符号表示二元或一元运算，称为算符.
2．表示二元或一元运算的方法: 解析公式和运算表
公式表示
运算表：表示有穷集上的一元和二元运算

定义9.3 设◦为S上的二元运算,
(1) 若对任意x,y∈S 有 x◦y=y◦x, 则称运算在S上满足交换律.
(2) 若对任意x,y,z∈S有 (x◦y)◦z=x◦(y◦z), 则称运算在S上满足结合律.
(3) 若对任意x∈S 有 x◦x=x, 则称运算在S上满足幂等律.
定义9.4 设◦和∗为S上两个不同的二元运算,
(1) 若对任意x,y,z∈S有 (x∗y)◦z=(x◦z)∗(y◦z)，
z◦(x∗y)=(z◦x)∗(z◦y), 则称◦运算对∗运算满足分配律.
(2) 若°和∗都可交换,且对任意x,y∈S有 x◦(x∗y)=x，x∗(x◦y)=x,
则称◦和∗运算满足吸收律.
定义9.5 设◦为S上的二元运算,
(1) 如果存在e_l(或e_r)S，使得对任意 x∈S 都有
e_l◦x = x (或 x◦e_r= x)，
则称e_l(或e_r)是S中关于◦运算的左(或右)单位元.
若e∈S关于◦运算既是左单位元又是右单位元，则称e为S上关于◦运算的单位元. 单位元也叫做幺元.
(2) 如果存在_l(或_r)∈S，使得对任意 x∈S 都有
_l◦x = _l (或 x◦ _r=  r)，
则称_l(或_r)是S 中关于◦运算的左(或右)零元.
若∈S 关于◦运算既是左零元又是右零元，则称为S上关于运算◦的零元.
(3) 设◦为S上的二元运算, 令e为S中关于运算°的单位元.
对于x∈S，如果存在y_l(或y_r)∈S使得
y_l◦x=e（或x◦y_r=e）
则称y_l(或 y_r)是x的左逆元（或右逆元）.
关于◦运算，若y∈S 既是 x 的左逆元又是 x 的右逆元，则称 y为x的逆元. 如果 x 的逆元存在，就称 x 是可逆的.
定理9.1 设◦为S上的二元运算，e_l和e_r分别为S中关于运算的左和右单位元，则e_l= e_r= e为S上关于◦运算的惟一的单位元.
注意：
当 |S|  2，单位元与零元是不同的；
当 |S| = 1时，这个元素既是单位元也是零元.
定理9.2 设◦为S上可结合的二元运算, e为该运算的单位元, 对于x∈S 如果存在左逆元 y_l和右逆元 y_r, 则有 y_l = y_r= y, 且 y是 x 的惟一的逆元.
说明：对于可结合的二元运算，可逆元素 x 只有惟一的逆元，记作 x^1
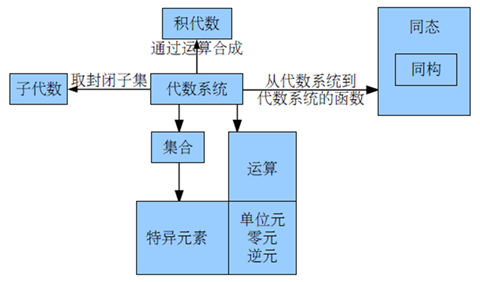
定义9.6 非空集合S和S上k个一元或二元运算f₁,f₂,…, f_k组成的系统称为代数系统, 简称代数，记做<S, f₁, f₂, …, f_k>.

构成代数系统的成分：
集合（也叫载体，规定了参与运算的元素）
运算（这里只讨论有限个二元和一元运算）
代数常数（通常是与运算相关的特异元素：如单位元等）研究代数系统时，如果把运算具有它的特异元素也作为系统的性质之一，那么这些特异元素可以作为系统的成分，叫做代数常数.
定义9.7
(1) 如果两个代数系统中运算的个数相同，对应运算的元数相同，且代数常数的个数也相同，则称它们是同类型的代数系统.
(2) 如果两个同类型的代数系统规定的运算性质也相同，则称为同种的代数系统.
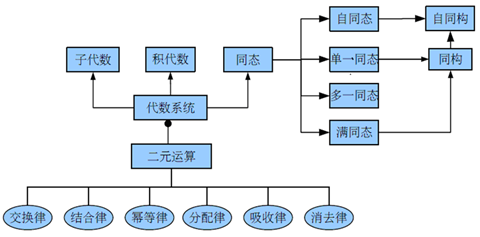
定义9.8设V=<S, f₁, f₂, …, f_k>是代数系统，B是S的非空子集，如果B对f₁, f₂, …, f_k都是封闭的，且B和S含有相同的代数常数，则称<B, f₁, f₂, …, f_k>是V的子代数系统，简称子代数. 有时将子代数系统简记为B.
子代数和原代数是同种的代数系统
对于任何代数系统V=<S, f₁, f₂, …, f_k>，其子代数一定存在.
(1) 最大的子代数：就是V本身
(2) 如果令V中所有代数常数构成的集合是B，且B对V中所有的运算都是封闭的，则B就构成了V的最小的子代数
(3) 最大和最小的子代数称为V 的平凡的子代数
(4) 若B是S的真子集，则B构成的子代数称为V的真子代数.
定义9.9 设V₁=<A,◦>和V₂=<B,>是同类型的代数系统，◦和为二元运算，在集合AB上如下定义二元运算▪， <a₁,b₁>,<a₂,b₂>AB，有<a₁,b₁>▪<a₂,b₂>=<a₁◦a₂, b₁b₂>
称V=<AB,▪ >为V₁与V₂的积代数，记作V₁V₂. 这时也称V₁和V₂为V的因子代数.
定理9.3 设V₁=<A,◦>和V₂=<B,>是同类型的代数系统，
V₁V₂=<AB,▪>是它们的积代数.
(1) 如果◦ 和 运算是可交换（可结合、幂等）的，那么▪运算也是可交换（可结合、幂等）的
(2) 如果 e₁和 e₂（₁和₂）分别为◦ 和 运算的单位元（零元），那么<e₁,e₂>（<₁,₂>）也是▪运算的单位元（零元）
(3) 如果 x 和 y 分别为◦和 运算的可逆元素，那么<x,y>也是▪运算的可逆元素，其逆元就是<x^¹,y^¹>
定义9.10 设V₁=<A,∘>和V₂=<B,>是同类型的代数系统，f:AB，且x, yA 有 f(x∘y) = f(x)f(y), 则称 f 是V₁到V₂的同态映射，简称同态.
同态分类：
(1) f 如果是单射，则称为单同态
(2) 如果是满射，则称为满同态，这时称V₂是V₁的同态像，记作V₁V₂
(3) 如果是双射，则称为同构，也称代数系统V₁同构于V₂，记作V₁V₂
(4) 如果V₁=V₂，则称作自同态