一阶滞后滤波

一阶滞后滤波

一阶滞后滤波的公式是：本次滤波结果 = 滤波系数(a) * 本次采集结果 + (1 - 滤波系数(a)) * 上次滤波结果

实际上可以看作是对本次的滤波结果进行了一个加权和，如果是滤波的系数越大，对本次采集的结果加权越重，上次的滤波结果加权也就没有那么重了

假设上次的滤波结果是10，这次的采集结果是20，产生了一个10的突变，如果使用一阶滞后滤波后，假设滤波系数是a = 0.7，本次的滤波值 = 0.7*20 + 0.3*10 = 17，使得突变没有那么严重，在滤去脉冲干扰的时候有很好的效果，一阶滞后滤波会使得到的数据波形比原波形更加的平缓

优缺点

优点：
对周期干扰有良好的抑制作用，适用于波动频率比较高的场合

缺点：
不适用于对实时性要求高的
相位滞后，灵敏度低
滞后程度取决于a值大小
不能消除滤波频率高于采样频率的1/2的干扰信号

matlab模拟

代码：

% 两个频率分别为15HZ 和 20HZ 的正弦信号
Fs = 90;    % 采样频率50Hz
f1 = 15;
f2 = 20;
f3 = 42;
t = 0:1:100;     % 0-9.98s 一共500个点
x = sin(2*pi*f1*t) + 0.5*sin(2*pi*f2*t) + 0.3*sin(2*pi*f3*t);   % 原始信号
N = length(x);          % N=500
figure(1);
title('时域信号');
xlabel('时间'); 
ylabel('幅值');
plot(t,x);
hold on
t1 = 1:1:101;
y1 = 0.7*x + 0.3*(sin(2*pi*f1*(t-1)) + 0.5*sin(2*pi*f2*(t-1)) + 0.3*sin(2*pi*f3*(t-1)));
plot(t1,y1);

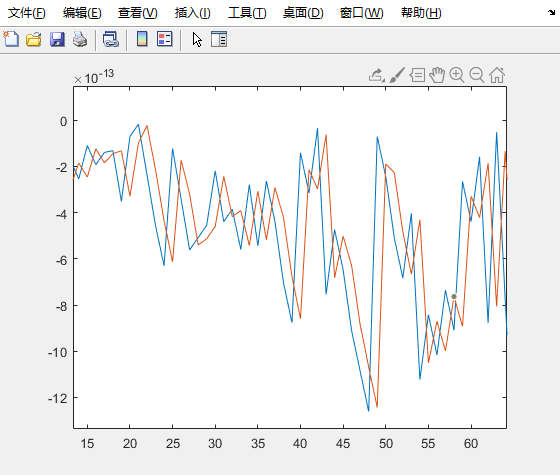
当a = 0.9的时候，一阶滞后滤波结果如下：

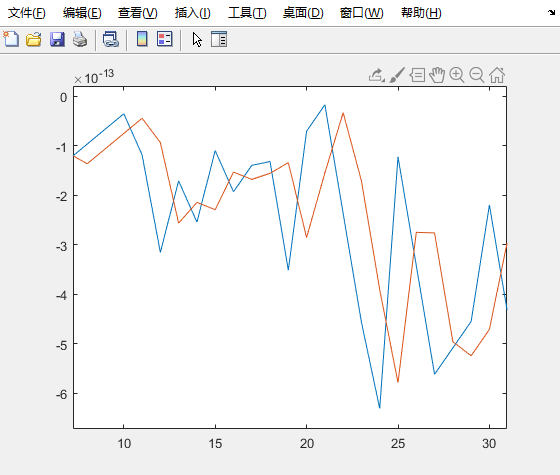
当a = 0.7的时候，一阶滞后滤波结果如下：

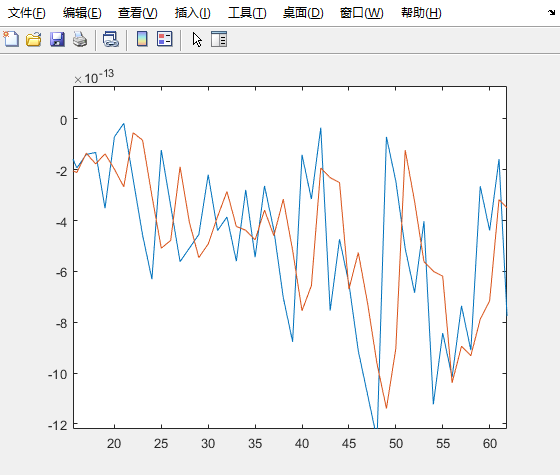
当a = 0.3的时候，一阶滞后滤波结果如下：

最后

以上就是勤劳夕阳为你收集整理的一阶滞后滤波的全部内容，希望文章能够帮你解决一阶滞后滤波所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。