概述
零. 收获
（1）理解偏差信号在控制系统分析中的核心作用；
（2）反馈控制带来的系统性能改善，如降低系统对模型参数不确定性的灵敏度、提高抑制干扰信号和测量噪声影响的能力；
（3）系统瞬态响应调控和稳态响应调控之间的区别；
（4）反馈控制对于控制系统性能的提升作用及必须的成本。
一. 概念强调
- 偏差信号
控制系统是由相互关联的开工至部件构成的，能够产生预期响应的系统。由于事先已知系统的预期输出响应，因此，在获得实际输出之后，就可以得到预期输出和实际输出之间的偏差。
2. 开环系统
开环系统不带有反馈，输入信号能直接激励产生输出响应。
3. 闭环系统
闭环系统将观测得到的输出信号与预期的输出信号进行比较，产生偏差信号，并通过控制器利用该信号来调节执行机构。
4. 系统灵敏度
系统灵敏度是指，当变化量为微小增量时，系统传递函数的变化率与受控对象传递函数（或参数）的变化率之比。
假设
则系统灵敏度定义为
当取微小增量的极限形式，可得
5. 瞬态响应
瞬态响应是控制系统最重要的特性之一，通常用时间函数来描述。
6. 稳态误差
稳态误差是指瞬态响应消失之后，系统的持续响应与预期响应的误差。
7. 分析中使用的符号
（1）前向通道传递函数
反馈通道传递函数
开环传递函数
闭环传递函数是表明闭环系统输出与输入的关系，对于负反馈系统，闭环传函=
（2）定义函数
（3）定义灵敏度函数S(s)
（4）定义补灵敏度函数C(s)
（5）灵敏度函数+补灵敏度函数 = 1
二. 基本知识
- 控制系统中的折中（幅值设计）
对于一个单回路的反馈控制系统而言，可以得到偏差信号，即跟踪误差信号为
代入各个函数
则当受控对象
一方面为了降低干扰信号
另一方面，为了降低衰减测量噪声
很明显，出于上述两个方面的考虑，在设计控制器
2. 引入反馈的作用
（1）能够降低系统对受控对象参数变化的灵敏度；
（2）提高系统抑制干扰信号的能力；
（3）提高系统衰减测量噪声的能力；
（4）减小系统的稳态误差；
（5）便于控制和调节系统的瞬态响应。
3. 反馈的代价
（1）增加了部件的数量，提高了系统的复杂度，并且在控制系统中，传感器往往是最昂贵的器件；
（2）引入反馈后的增益损失。对一个单环系统而言，开环增益为
即我们宁愿损失一定的开环增益来换取对系统响应的调控能力。
（3）可能会导致系统具有不稳定性。即使开环系统是稳定的，相应的闭环系统也可能会失稳。
三. 使用matlab来分析控制系统的特性
- 分析开环系统对阶跃干扰信号的响应
% Analysis of the open-loop speed control system.
%
Ra=1; Km=10; J=2; f=0.5; Kb=0.1;
num1=[1]; den1=[J f]; sys1=tf(num1,den1);
num2=[Km*Kb/Ra]; den2=[1]; sys2=tf(num2,den2);
sys_o=feedback(sys1,sys2);
%
% Change sign of transfer function since
% disturbance has negative sign in the block diagram
%
sys_o=-sys_o
%
% Compute time response to a unit step disturbance
%
[yo,T,xo]=step(sys_o);
plot(T,yo)
title('Open-loop Disturbance Step Response')
xlabel('Time (sec)'), ylabel('omega_o'), grid
%
% Steady-state error -> last value of output yo
%
yo(length(T))
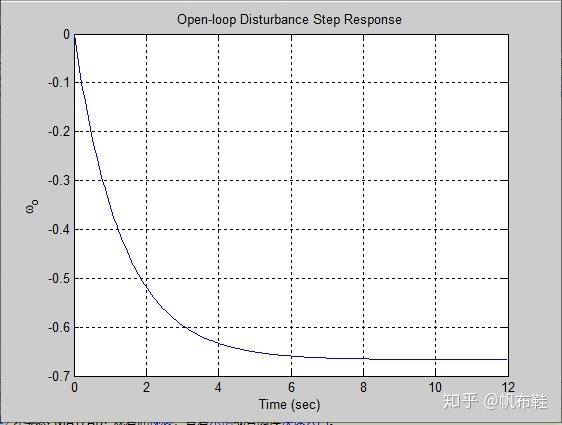
2. 闭环系统对阶跃告饶信号的响应
% Analysis of the closed-loop speed control system.
%
Ra=1; Km=10; J=2; f=0.5; Kb=0.1; Ka=54; Kt=1;
num1=[1]; den1=[J,f]; sys1=tf(num1,den1);
num2=[Ka*Kt]; den2=[1]; sys2=tf(num2,den2);
num3=[Kb]; den3=[1]; sys3=tf(num3,den3);
num4=[Km/Ra]; den4=[1]; sys4=tf(num4,den4);
sysa=parallel(sys2,sys3);
sysb=series(sysa,sys4);
sys_c=feedback(sys1,sysb);
%
% Change sign of transfer function since disturbance
% enters with negative sign in the block diagram
%
sys_c=-sys_c
%
% Compute time response to a unit step disturbance
%
[yc,T,xc]=step(sys_c);
plot(T,yc)
title('Closed-loop Disturbance Step Response')
xlabel('Time (sec)'), ylabel('omega_c (rad/sec)'), grid
%
% Steady-state error -> last value of output vector yc
%
yc(length(T))
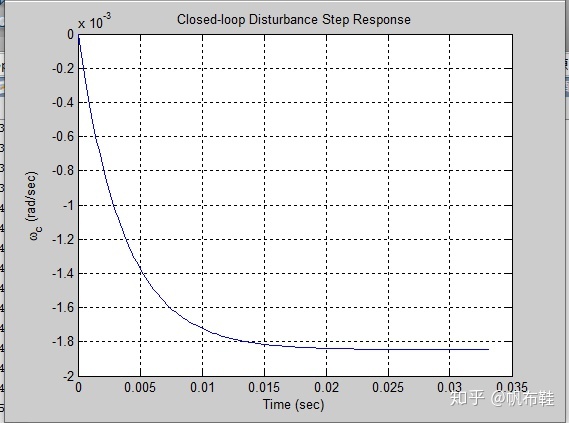
从图中显示，在开换系统中引入负反馈环节，显著地降低了干扰对输出的影响。这说明闭环反馈系统具备良好的干扰抑制能力。
3.不同取值的控制器增益k对系统的影响
分析系统方程为：
% English channel boring machine: step response
% for K=100 and K=20.
%
numg=[1]; deng=[1 1 0]; sysg=tf(numg,deng);
K1=100; K2=20;
num1=[11 K1]; num2=[11 K2]; den=[0 1];
sys1=tf(num1,den);
sys2=tf(num2,den);
%
% Compute closed-loop transfer functions
%
sysa=series(sys1,sysg); sysb=series(sys2,sysg);
sysc=feedback(sysa,[1]); sysd=feedback(sysb,[1]);
%
% Plot step response
%
t=[0:0.01:2.0];
[y1,t,x]=step(sysc,t); [y2,t,x]=step(sysd,t);
subplot(211), plot(t,y1), title('Step Response for K=100')
xlabel('Time (sec)'),ylabel('y(t)'), grid
subplot(212),plot(t,y2), title('Step Response for K=20')
xlabel('Time (sec)'),ylabel('y(t)'), grid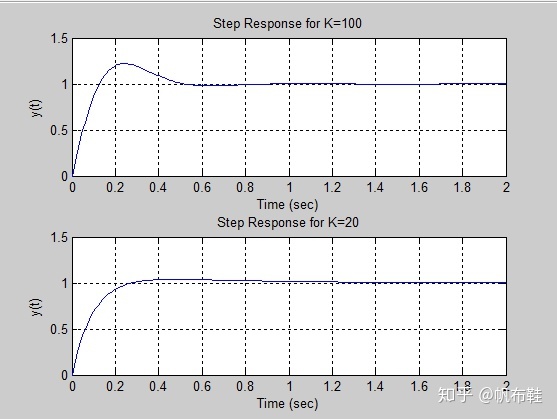
从曲线中看出，增益K越小，系统的超调量也就越小，说明反馈控制增益K的确能够调节系统的瞬态响应特性。如果单单从瞬态响应角度拉看，K=20会更加适合。还需要考虑系统对单位阶跃干扰信号的响应。
% Response to a Disturbance D(s)=1/s for K=20 and K=100
%
numg=[1]; deng=[1 1 0];
sysg=tf(numg,deng);
K1=100; K2=20;
num1=[11 K1]; num2=[11 K2]; den=[0 1];
sys1=tf(num1,den); sys2=tf(num2,den);
%
% Compute closed-loop transfer functions
%
sysa=feedback(sysg,sys1); sysa=minreal(sysa);
sysb=feedback(sysg,sys2); sysb=minreal(sysb);
%
% Plot step response
%
t=[0:0.01:2.5];
[y1,t,x]=step(sysa,t); [y2,t,x]=step(sysb,t);
subplot(211), plot(t,y1), title('Disturbance Response for K=100')
xlabel('Time (sec)'),ylabel('y(t)'), grid
subplot(212),plot(t,y2), title('Disturbance Response for K=20')
xlabel('Time (sec)'),ylabel('y(t)'), grid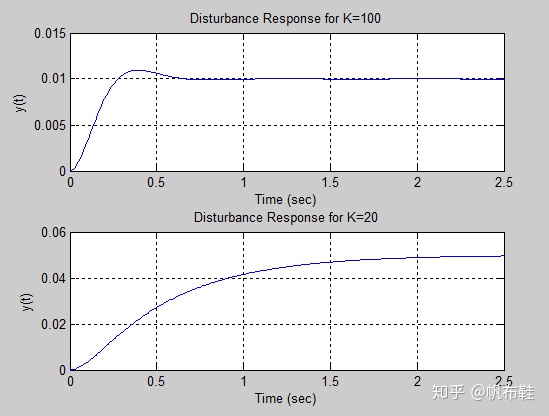
K值越大，则系统的单位阶跃干扰的稳态响应y(t)越小，则仅仅考虑系统抑制干扰的能力，应该选择K=100.
在本例中，增大增益K意味着能够更好的抑制干扰，而减小增益则能够改善系统的瞬态性能（如降低系统的超调量）。最后必须由设计者根据具体情况来确定最后的增益K
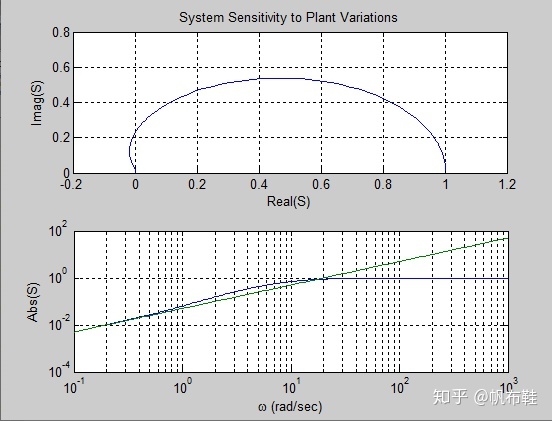
4. 系统的灵敏度
% English channel boring machine: system sensitivity
% for K=20.
%
K=20; num=[1 1 0]; den=[1 12 K];
w=logspace(-1,3,200); s=w*j;
%
% Compute System Sensitivity
%
n= s.^2 + s; d= s.^2 +12*s+K; S=n./d;
%
% Compute Approximate Sensitivity S = s / K
%
n2= s; d2=K; S2=n2./d2;
%
% Generate the plots
%
subplot(211), plot(real(S),imag(S))
title('System Sensitivity to Plant Variations')
xlabel('Real(S)'), ylabel('Imag(S)'), grid
subplot(212), loglog(w,abs(S),w,abs(S2))
xlabel('omega (rad/sec)'), ylabel('Abs(S)'), grid
5. 循序渐进设计实例
本次讨论磁盘驱动器对干扰和系统参数变化的响应特性，当调节放大器增益
（1）当调节放大器增益
当Ka=10时的系统瞬态响应
% Compute the input step response for Ka=10.
% Results shown in Figure 4.34 (b).
% Select Ka=80 to obtain the corresponding step response.
%
Ka=10;
nf=[5000]; df=[1 1000]; sysf=tf(nf,df);
ng=[1]; dg=[1 20 0]; sysg=tf(ng,dg);
sysa=series(Ka*sysf,sysg);
sys=feedback(sysa,[1]);
t=[0:0.01:2];
step(sys,t);
ylabel('y(t)'), xlabel('Time (sec)'), grid
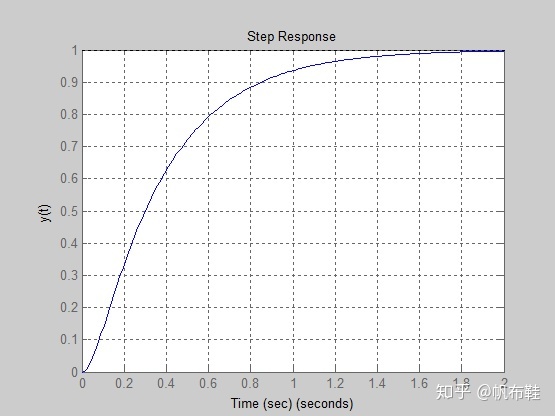
当调整Ka=80时，可以得到瞬态响应
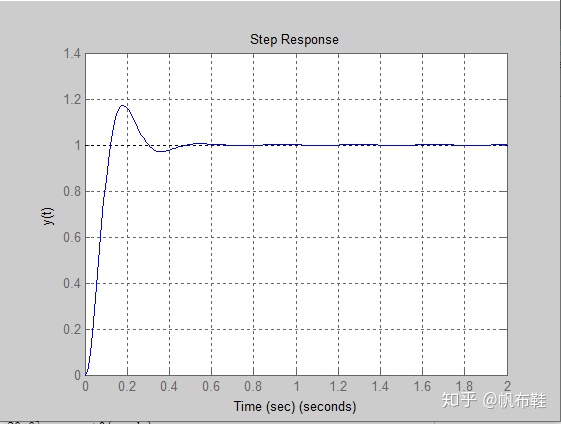
则相比较放大器增益Ka=10时，Ka=80时，系统对输入指令的响应速度明显加快，但响应过程中会出现振荡。
（2）再来分析范围阶跃干扰信号
% Compute the disturbance response for Ka=80.
% Results shown in Figure 4.35 (b)
%
Ka=80;
nf=[5000]; df=[1 1000]; sysf=tf(nf,df);
ng=[1]; dg=[1 20 0]; sysg=tf(ng,dg);
sys=feedback(sysg,Ka*sysf);
sys=-sys;
t=[0:0.01:2];
step(sys,t);
ylabel('y(t)'), xlabel('Time (sec)'), grid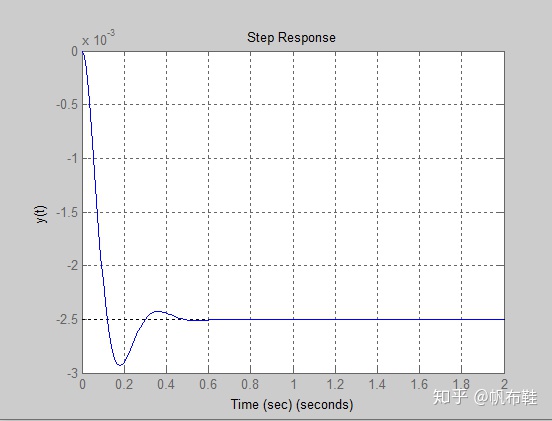
如果想进一步降低干扰对系统的影响，就必须将Ka增大到80以上，但是，这将导致系统的单位阶跃响应中出现不可接受的振荡。
那么如何选择增益Ka的最优值，确保系统响应既快速又不会出现振荡呢？
最后
以上就是虚幻帆布鞋为你收集整理的matlab step函数_反馈控制系统的特性与matlab的计算指令的全部内容，希望文章能够帮你解决matlab step函数_反馈控制系统的特性与matlab的计算指令所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复