matlab求系统根轨迹代码_要想正确画出根轨迹，先搞清楚这8大法则再说！

话说宝刀君这几年给学弟学妹们辅导自控时，学弟学妹们面对根轨迹，经常是一脸懵逼。

常常是拿到题后，零极点都标出来了，法则也写出来了，但就是根轨迹画不出来。

有时好不容易画出来了，返回去和法则一对照，忍不住仰天长叹：

我靠，怎么对应不上呀？

蓝瘦，香菇！

其实上面描述的情形，大部分学生都存在，而且还不在少数.......

为了拯救学弟学妹们，为了更好地传播大师前辈们在根轨迹上做出的努力，宝刀君就继续拾人牙慧，写点我的理解，今天给大家奉献纯干货笔记---深入讲解根轨迹的绘制法则！

大家可以对照着看，测测你理解到什么程度。

哦，对了，我使用的教材是卢京潮老师主编，西北工业大学出版社的《自动控制原理》（第2版），身为西工大的求学一份子，替卢老师宣传下他的书，主要是确实质量好啊！

好了，言归正传，先送上宝刀君的笔记美图：

还是熟悉的话语，熟悉的字样，熟悉的公式，可我就是不知道他在说什么，呜呜呜......

上面呢，就是宝刀君手抄的笔记，里面附带了一些疑问，个人觉得这些疑问就是你在学习时就应该仔细思考的，只要你复习时把这些疑问都搞懂了，那根轨迹学的不会太差。

今天我们就从第一条法则开始，逐句解读这八大法则，包你看完心情爽歪歪！

先看第1条：根轨迹的起点和终点

这条呢，其实是告诉你根轨迹从哪来，到哪里去？

每一条根轨迹从极点出发，然后终止于零点或者终止于无穷远处，然后呢，终止于无穷远处的根轨迹条数也给你说了，是n-m条。

说简单点，就是起源有1处，去向有2处~

再看第2条：根轨迹的分支数、对称性、连续性

这个法则呢，是说你画的根轨迹有几条，条数等于n或者m，谁大取谁。然后你画的根轨迹是对称于实轴的，根轨迹线肯定是连续的，不能画成断点的形式。

第3条：实轴上的根轨迹 （这条真重要！）

仔细看笔记上对这条的官方定义，什么叫“若其右边”？

后边的那几个问题你能回答上来几个？

要想明白这个问题，得先明白这个实轴的区域是怎么划分的。

设想一下，给你一个标准型开环传递函数，就是首1型的传递函数形式，那你就可以立马确定出他的零极点，然后在复域平面上标出来，落在实轴上的零极点，刚好将实轴从负无穷到正无穷分成了若干个小区间，那么现在的问题是：实轴上的这些小区间，哪些是根轨迹经过的？

法则给出了答案，即对于绘制180度的根轨迹来说，只要这个区间的右边零极点个数之和为奇数，那么这段区间就是根轨迹。

到这里，又有问题了。

因为我们知道每一个区间都有左右端点，这里的“若其右边”，数数时，包不包含这个小区间的右端点呢？

答案是：包含！

举个栗子，诺，你看笔记里写的那个开环传递函数，它没有零点，只有三个极点，分别是p1=0,p2=-1,p3=-5。

这三个极点将实轴分成了（负无穷，-5]，(-5,-1]，(-1,0]，(0,正无穷）这4个区间。

现在你给我从左至右，挨个判断这4个区间哪个是根轨迹！

好，先从第一个开始，在第一个区间（负无穷，-5]的右边有3个极点，分别是-5，-1，0。刚好是奇数，按照法则，这个区间（负无穷，-5]是根轨迹。

紧接着判断第二个区间(-5,-1]，他的右边只有-1和0两个极点，偶数，不满足，则不是根轨迹。

接着看(-1,0]，右边有一个极点0，是奇数个，则这个区间是根轨迹。

最后是(0,正无穷）的判断，右边为0个零极点，偶数个，则不是根轨迹。

所以，这个开环传递函数的实轴上的根轨迹是（负无穷，-5]，[-1,0]。

咳咳，这个法则有什么用？

这用处大了去了！

你想啊！首先你可以在画出零极点后，立马画出极点的指向，确定出位于实轴上的根轨迹呀，其次是将来算完分离点之后，分离点一般是二次方程会求出两个根，这时候你就可以根据这条规则，将那个不在实轴上的根轨迹范围的 根 给我舍去！

（注意了，我可没说分离点一定不在实轴上）

哎呀，说完这个，挺累，我喝口水先。

第4条：根轨迹的渐近线

这条呢，记住公式会写，需要注意的是： 你的角度求出来凡是-180到180度内的，那这些角度都是渐近线的角度，不能落下。

因为是对称于实轴嘛，所以负180度到180度的也算。

我为什么强调这点呢，原因是看见好多学生做这个时，若n-m=4，好多学生无缘无故的将正负3pai/4给我舍去了！

你有何种理由舍去？？？

第5条：根轨迹的分离点

矮油，这个规则也是重要的不得了呀！

前面说过，求出分离点后，利用法则3来进行取舍，那怎样列方程来求？举例如下，看图：

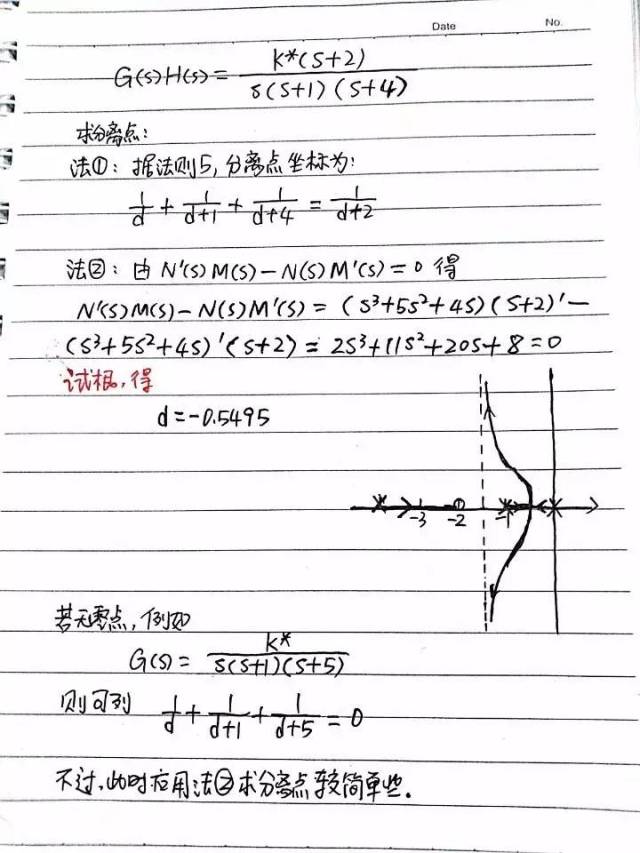
看上面这个图，相信你应该法1就会用了，需要注意的是法1在没有零点时，右边要写成0，没有零点就写0嘛，而从我辅导时实际测试学生来看，有些学生不知咋回事给我写个1 ！！！

看这篇笔记的学生注意啦！希望你别犯这个错误！

还剩一个问题没有解答，方程如何试根？？？

别愁，宝刀君都会给你讲的~

它这个分离点呢，是两个极点在运动相遇后又分离产生的。

所以呢，你现在就要找那些靠的很近的极点。

一般来说，两个相距很近的极点会产生分离点

你现在仔细看看上图和对照课本上所有有分离点的图，看看是不是这个规律！

因此呢，你挺好了，以后你试根的时候，就先用靠的很近的两极点的中间值来试，试完1次后，再延续二分法的思想，继续试。

比如介于-1和0时，我先试-0.5，再试-0.55，以此类推，最终使结果越趋近于0越好。

这就是求分离点时试根法的思想！

顺便说一句，当你求出分离点时，分离点处那个根轨迹增益Kd*你也顺带着求出来，分离点处的根轨迹增益叫做：临界阻尼根轨迹增益。

这个往往在写稳定欠阻尼范围时会用到哦！这里我仅仅抛砖引玉，你可以翻书看看之前碰过这种题型没。

第6条：根轨迹与虚轴交点

这个法则就是笔记上讲的，把s一换，分别令实部虚部等于0就行，虽然也有用劳斯判据来求的，但个人觉得还是这种代数方法简单好求。

对了，根轨迹与虚轴交点处的根轨迹增益K1*有个名字，叫做：临界稳定根轨迹增益。

如果人家让你求：给出系统在欠阻尼情况下的开环增益范围？有些学生直接给出 Kd*<K*<K1*。

真是大错特错！！！

看清题了没？

明白了吗？

人家问的是开环增益范围，所以你还得根据根轨迹增益和开环增益的转换公式，换算开环增益呐~

第7条：根轨迹的起始角和终止角

讲真，这个规则也不是随随便便用的，只有当出现复数零极点时，才会考虑用此规则！

很多漂亮的学妹在使用这个规则时，常常将角度算错，本来是加的，愣是给弄了个减，这本质是不清楚待求的角度该放在相角条件公式中的哪个位置。

看定义，它说这两个角度都是通过相角条件求的。

那什么是相角条件？

很简单，即分子的角度之和减去分母的角度之和=（2K+1）*pai（180度根轨迹）

换句话说，就是零点的角度之和减去极点的角度之和。

好！你先记住这个概念！

起始角指的是从极点出发的角，终止角指的是终止于零点的角度，那么我们这里可以这样理解，起始角看成极点角，终止角看成零点角。

那么，接下来你在列式子时，只需要将同类型的角度放在一块就好了。这样就可以避免求错！

第8条：根之和

开环极点之和=闭环极点之和。

这个规则和第7个规则一样，不适随随便便就能用的，都是有条件的，什么条件？

n-m>2时!

宝刀君在这里叮咛大家一句话：只要你拿到手的开环传递函数中分子分母差的阶数太多，那你就要注意啦，很可能要用到根之和法则！！！

建议出现这种情况时，顺手写在旁边，以防忘记！

这个法则有什么用？

答案是求根！

求什么根？

求某增益对应的其他根，一般是对于一个3阶系统，一对复数根知道后，接下来第3个根可以通过这个法则求（数学上，n阶系统对应n个根，自控里，根就对应的是闭环极点）。

举个栗子，前面第6条法则可以求出此时与虚轴的交点。假如是个3阶系统，此时题目中问你：求临界根轨迹增益对应的三个闭环极点？

好了，此时若满足根之和法则的应用条件，则可以应用此法则快速的求出第三个根！

为啥是第3个，因为你已经知道了2个了呀！那个与虚轴的交点不就是两个闭环极点嘛！

所以公式左侧只有1个未知数，而公式右侧的开环极点之和你也能一步写出来，因为开环传递函数你也知道呀，理解了这一点，就知道这个公式咋用了。

宝刀君觉得好多学生不会列式子，其实是概念不清晰，即还是不太理解根轨迹到底是个什么东东？

通俗说一下，根轨迹就是当某一参数变化时，系统的闭环特征方程所对应的根 随参数变化而变化 形成的轨迹。这就类似于数学上y随着x的变化而变化，描点画图形成的线嘛。

根轨迹上每一个点，对应闭环特征方程的一个根，对应闭环系统的某一个极点，这三个是 一 一对应的！

奉上绘制根轨迹的法则的一个汇总表吧，课本上的，看下图！

以上就是关于绘制根轨迹的所有法则，我想我应该说的很明白了，尤其是从第3条往后。

上面所列的法则，1234基本都有，5678看情况用。

当你绘制完根轨迹后，你要做的就是用绘出来的图检验它是否满足写的每个规则，当然，除非你规则都算错、写错，那就另当别论了......

说个敏感的问题，考试时根轨迹如何阅卷？

这个呀，看情况了，老师很可能先看你图画的对不对，图不正确的话，那么规则肯定是错的，因为你的图是根据规则画出来的，图都不对了，看那个规则有啥用呀，直接0分......相反，图对了，规则肯定正确，直接满分......

当然，也有一些老师比较仁慈，即使你画错了，她如果时间还多，估计会看看你前面那几条，如果有对的，就 酌情 给点分......

这就是酌情的意思

关于根轨迹，如果你有其他的理解角度、新颖想法，欢迎文章下方留言，大家一起学习交流哦

~

注：以上图片截图来自于电影《三傻大闹宝莱坞》

也许你还想看：

考研院校专业课选择及自动控制原理备考的宏观战略分析（一）

考研院校专业课选择及自动控制原理备考的宏观战略分析（二）

————————————————————END——————————————————

想看宝刀君更多的原创文章吗？

请关注宝刀君的微信公众号（ID：BDJ0501），那儿才是我的主要根据地~

关于：考研摆渡人宝刀君（BDJ0501）

工科自动化专业出身，

除了会 本专业 自动控制原理，

还钻研了下 考研数学

希望我分享的知识点对你的学习有帮助~