奈氏判据的推导

奈氏判据

同样判断一个系统是否稳定的方法有:

• 赫尔维茨判据
• 劳斯判据
• 根据根轨迹判断

本篇文章记录一下奈氏判据的推导方法。

假设开环传递函数已知，为：
$$G(s)H(s)=\frac{B(s)}{A(s)}$$
则其对应的闭环传递函数为：
$$\frac{G(s)}{1+G(s)H(s)}=\frac{A(s)G(s)}{A(s)+B(s)}$$
注：其中$A(s)$与$B(s)$均为多项式，并且阶次：
$$N_A>N_B$$

辅助函数

构造辅助函数：
$$F(s)=1+G(s)H(s)=\frac{A(s)+B(s)}{A(s)}$$
这样构造函数的理由是，该函数的零点是闭环传递函数的极点，极点是开环传递函数的极点。

幅角原理

设复平面$s$上，闭合曲线$\Gamma$包围$F(s)$的$Z$个零点和$P$个极点，则$s$沿$\Gamma$顺时针运动一周时，在根据映射$F$将$s$映射到$F(s)$平面上的闭合曲线${\Gamma }_F$，${\Gamma }_F$包围原点的圈数为：
$$R=P-Z$$
$R<0$与$R>0$分别表示${\Gamma }_F$顺时针和逆时针包围$F(s)$平面的原点，$R=0$表示没有点包围$F(s)$平面的原点。

这个原理反过来也是成立的，既可以从$s$平面闭合曲线$\Gamma$（自变量）的所包围的零极点个数之差推出$F(s)$平面闭合曲线${\Gamma }_F$（因变量）围绕原点的圈数，也能从$F(s)$平面闭合曲线${\Gamma }_F$（因变量）围绕原点的圈数推出$s$平面闭合曲线$\Gamma$（自变量）的所包围的零极点个数之差，奈氏判据用的就是逆向结论。

分析

注意我们刚刚构造的辅助函数：

巧合的是将辅助函数$F(s)$曲线在复平面向左平移一个单位，就是开环传递函数$G(s)H(s)$的曲线！围绕原点的旋转圈数转换为了围绕（-1，0）的旋转圈数；

换句话说，如果已知$G(s)H(s)$，画出开环幅相曲线，就等于知道了$R$和$P$的个数，$Z$也就求出来了，我们根据开环传递函数判断出了闭环传递函数的稳定性！

闭合曲线的选取

我们选取$s$平面上如下闭合曲线$\Gamma$：

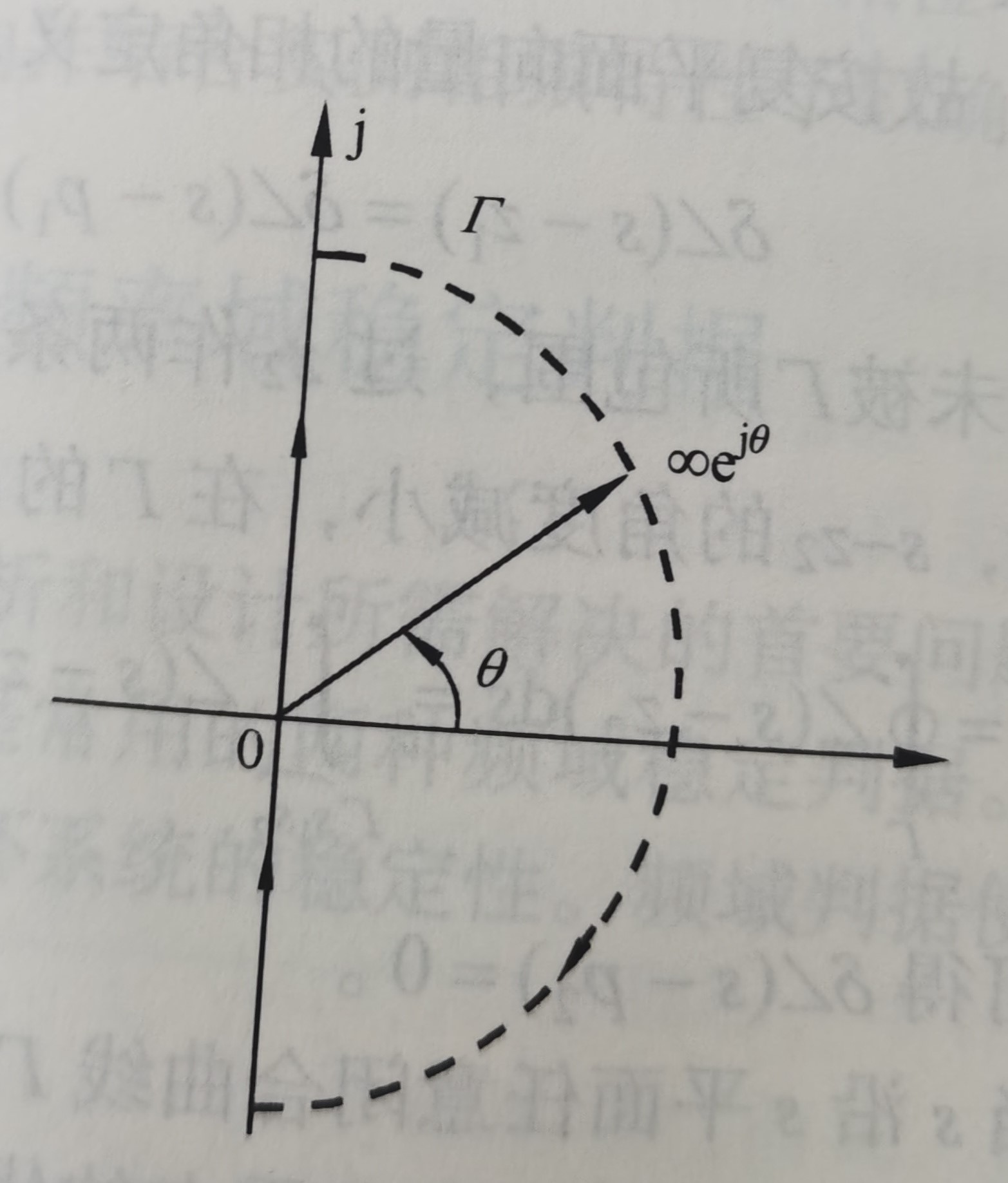
目的是为了包含整个右半平面，这样开环幅相曲线围绕（-1，0）点的圈数，就是在$s$平面的闭合曲线$\Gamma$包围（即整个正半平面）的零极点个数的差值$R$，由于开环传递函数$G(s)H(s)$的极点个数$P$已知，所以：
$$Z=P-R$$

结论

• 如果$Z=0$，闭环传递函数在$s$正半平面没有极点，系统稳定；

• 如果$Z>0$，闭环传递函数在$s$正半平面有极点，系统不稳定。

有趣的现象

• 由于多项式阶数$N_A>N_B$，$\Gamma$上的虚线部分幅值为$+\infty$，所以虚线上的点映射到$F(s)$上之后，都汇聚在了$F(s)$平面的原点。
• 如果存在积分环节，那么$\omega =0^{-}\to 0^{+}$时，${\Gamma }_F$上跨越了无穷远的路径。（下图中蓝色虚线部分$\omega =0\to 0^{+}$）

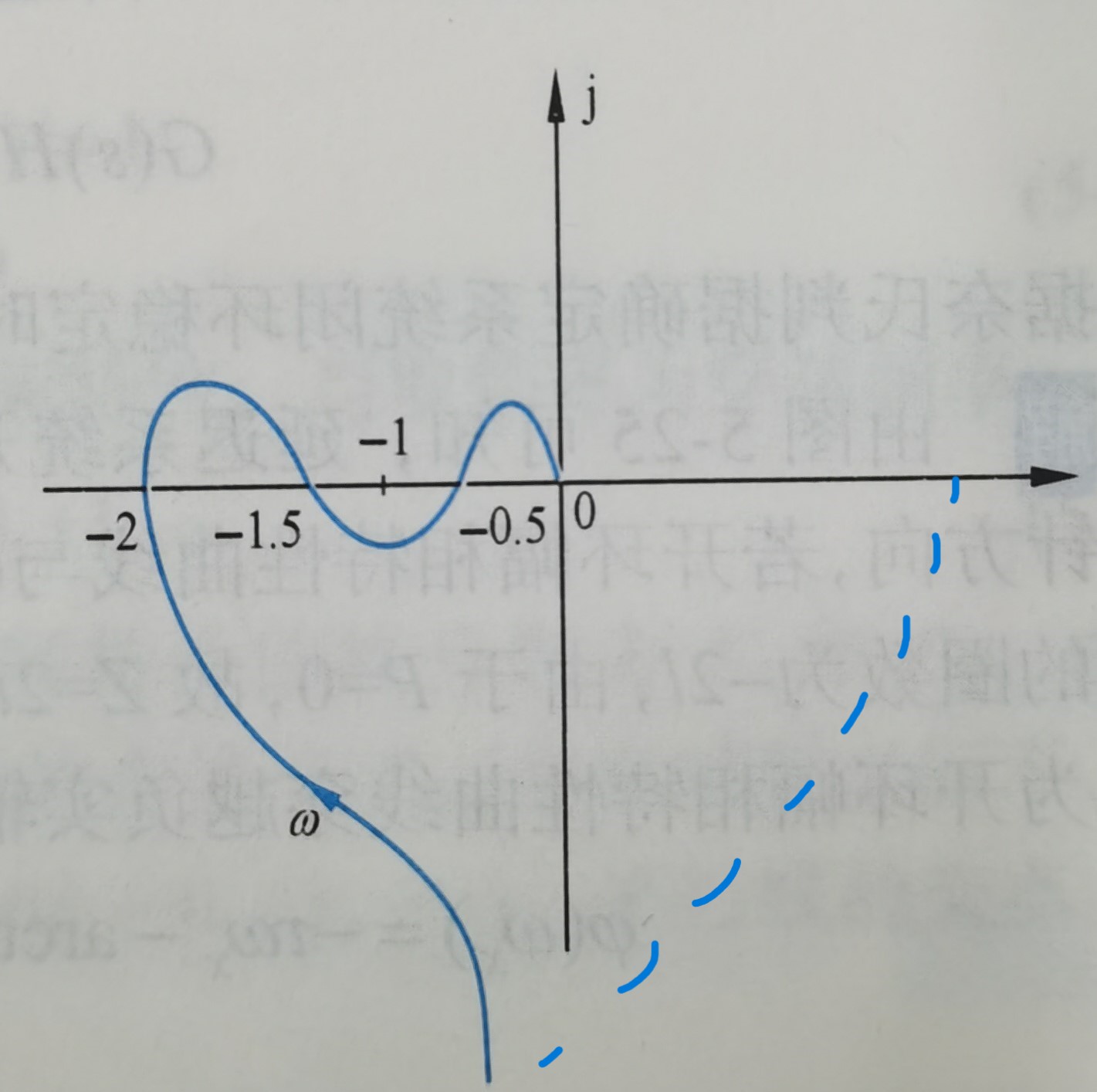
最后

以上就是畅快网络为你收集整理的奈氏判据的推导的全部内容，希望文章能够帮你解决奈氏判据的推导所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。