香农定理和奈奎斯特定理区别_这一切都从指数函数开始（4）——采样定理

系列目录：

TravorLZH：这一切都从指数函数开始（1）——欧拉公式

TravorLZH：这一切都从指数函数开始（2）——Fourier级数和变换

TravorLZH：这一切都从指数函数开始（3）——泊松求和公式

信号处理领域中有一个基本的定理——采样定理。这个定理在最早提出时还顺便提供了一个副产品：Whittaker—Shannon插值公式，本篇文章作者将以循序渐进的方式推导出采样定理。

1、采样定理

设一个函数f(t)的Fourier变换

满足如下条件：

当

或者是

时

恒等于零

我们可以通过对

做Fourier逆变换的方式来得到原来的f(t)：

应用上面我们对频域

的限制，我们可以安全地把积分上下限从(-∞,+∞)改成[-B,B]因为该区间外

恒为零。于是：

此时我们若令

，则有：

等式两侧再除以2B，得：

此时我们设T=2B，可以发现：

再令

，得到

现在我们再利用一下我之前得到关于Fourier级数的结论：

对于

，有

则可以发现

可以表示为：

意思就是说我们可以用函数无穷个等距的点来换元其频域，其中点的间距为

，因为频域确定后时域也能够通过逆变换的方法确认，所以我们得到如下定理：

If a function contains no frequencies higher than B hertz, it is completely determined by giving its ordinates at a series of points spaced

seconds apart.

^[1]
如果一个函数f(t)的频率不超过B赫兹，则f(t)可以被一系列间距为

秒的采样点确定。

2、插值公式

现在我们已经证明了采样定理，现在我们可以再进一步研究这个等式：

现在我们对两侧进行Fourier逆变换：

根据控制收敛定理（Dominated convergence theorem），我们可以交换求和与积分符号。又根据上面对频域的限制条件，即

，积分的上下限可以变成[-T/2,T/2]（即[-B,B]）。于是：

接下来我们解一下右侧剩下的积分

根据积分法则

我们可以得到

根据欧拉公式，我们有

，所以

我们最后再把积分的结果代入回原来的等式，得：

我们知道sinc函数的定义

，所以可以把它代入原式：

现在令n=-k，M=1/T，得到：

此时根据T=2B，我们知道M=1/2B表示采样点间隔秒数，所以可以将f(Mn)写成f的第n个采样点f[n]，于是：

我们重新得到了大名鼎鼎的惠特克—香农插值公式（Whittaker—Shannon interpolation formula）。

通过我们推导出的采样定理，我们也得知了一个新概念——混叠（Aliasing）。

3、混叠效应

如果我们尝试对一个不满足采样定理条件的函数进行插值，则会出现混叠。这里我们可以用Python来演示：

首先我们定义要被插值的函数：

def 

接下来我们对其进行采样

interval

现在再利用插值公式还原信号：

def 

最后我们在用numpy和matplotlib把原本的函数与插值公式恢复的信号进行对比：

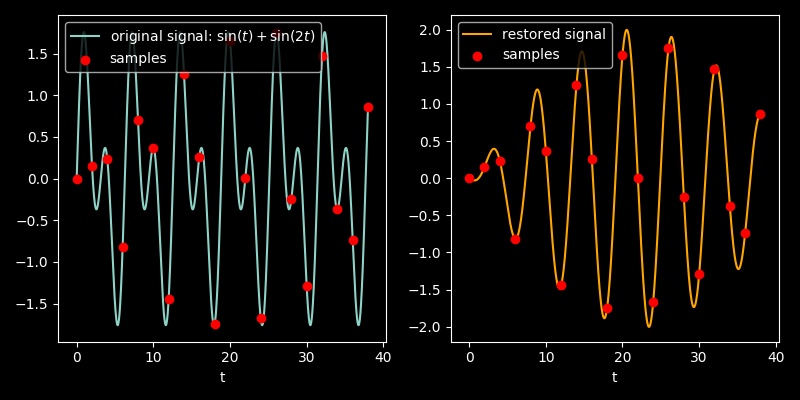
import 

最后我们生成了这幅图，其中左侧是原来的函数，右侧是根据红色采样点恢复的结果：

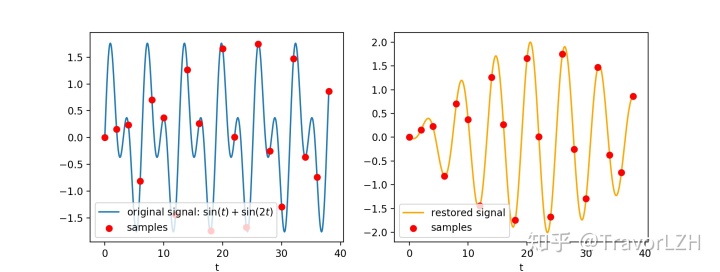
当我们对原信号

进行Fourier变换时，得到：

而采样点的间距通过

我们可以得到B=1/4，然而我们发现

在

时不恒为0（

取

和

时

为+∞），所以就出现了混叠效应。

然而当我们让B=1时（即M=1/2时），却发现插值公式可以还原原来的函数：

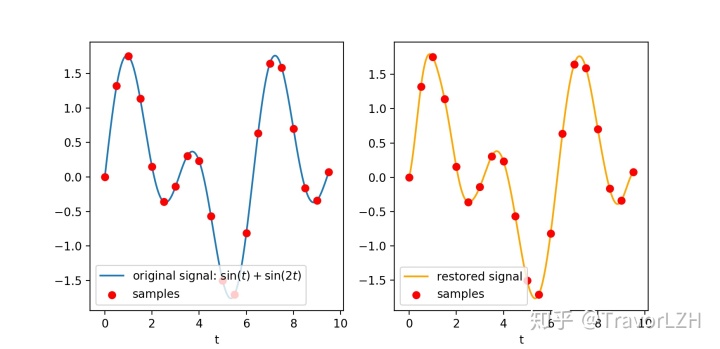
4、总结

采样定理不仅本身非常的迷人，它的来源也非常的奇妙。为了证明采样定理，我们利用了Fourier变换；为了得出Fourier变换，我们拓展了Fourier级数；为了推导Fourier级数，我们运用了欧拉公式；为了推导欧拉公式，我们利用了指数函数的微分性质……可见这一切都从指数函数开始。

参考

1. ^https://en.wikipedia.org/wiki/Nyquist%E2%80%93Shannon_sampling_theorem