自控原理学习笔记
自控原理学习笔记专栏
文章目录
- 1.频率特性函数
- 1.1 图形表示方法:
- 1.2 零极点位置和暂态增益图
- 1.2.1 复轨迹曲线
- 1.2.3 例子
- 1.3 计算系统响应
- 2.开环频率特性幅相曲线
- 2.1 典型环节幅相曲线-Nyquist图
- 2.2一般特性频率曲线
- 2.2.1 开环传递函数:
- 2.2.2 幅相曲线的绘制:
- 2.2.3 特征点
- 2.2.4 例子
- 3.开环对数频率特性
- 3.1Bode图概念
- 3.2 典型环节Bode图
- 3.3 Bode图渐近线画法:
- 3.4最小相位系统:
- 3.5举例
1.频率特性函数
对于稳定的线性时不变系统(LTI),
-
频率特性:
- 系统稳态输出与输入信号的复数比
- 系统输出信号与输入信号Fouier变换之比
-
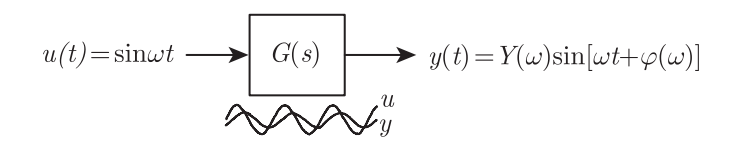
对于稳定的LTI,若R(t)为正弦信号,则y(t)为同频率正弦信号。
-
物理意义:表征系统对不同频率正弦输入响应特性
-
频率特性函数实质:复变函数
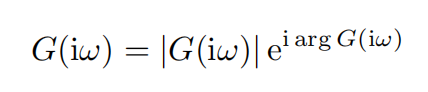
幅 频 : A ( w ) = ∣ G ( i w ) ∣ 相 频 : φ ( w ) = a r g G ( i w ) 幅频:A(w)=|G(iw)|\ 相频:varphi (w)= arg G(iw) 幅频:A(w)=∣G(iw)∣相频:φ(w)=argG(iw)
1.1 图形表示方法:
Nyquist图----特点:
1)具有对称性; 2)已知开环频率特性L(iω),可令w由小到大取值,算出幅值 | L(iω )| 和相位∠L (iω) 的相应值,在 L 平面描点绘图,可以得到开环幅相曲线。
Bode 图----特点:
1)可展宽幅频范围; 2)可简化作图过程; 3)便于图解应用; 4)难以应用于系统稳定性定理的证明
Nichols图---- 特点:
1)系统增益的改变,不影响相频特性,故增益改变时,对数幅相特性只是简单的向上平移或向下平移,而曲线形状保持不变; 2)G(iω)和1/G(iω)的对数幅相特性图相对原点中心对称,即幅值和相位均相差一个符号; 3)利用对数幅相特性图,很容易由开环频率特性求闭环频率特性,可方便地用于确定闭环系统的稳定性及解决系统的综合校正问题。
1.2 零极点位置和暂态增益图
1.2.1 复轨迹曲线
按广义频率特性,令s=iw,可得到开环系统的复轨迹曲线,可表示为:
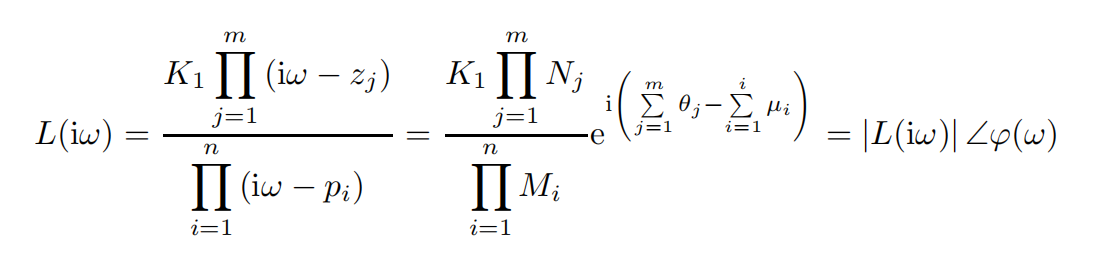
-
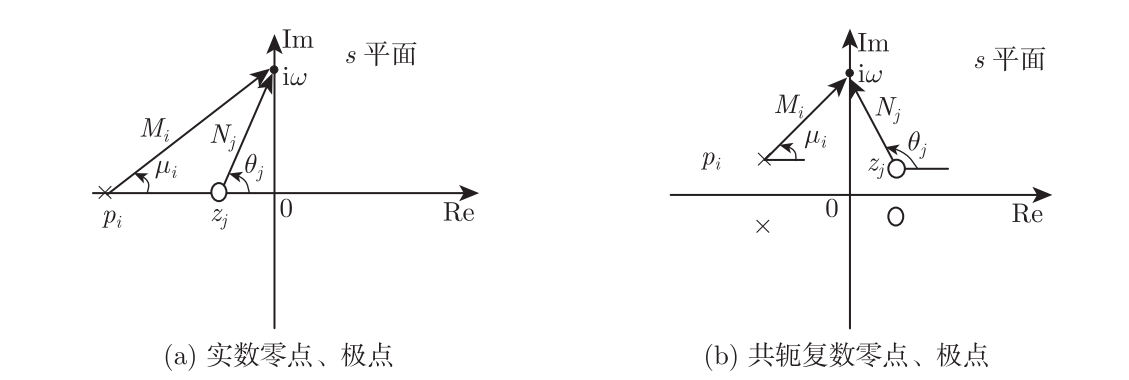
极点矢量 p i p_i pi:分母因式(iw-p_i)是s平面从极点指向虚轴上iw的矢量。
-
零点矢量 z j z_j zj: 分子因式(iw-z_j)是s平面从零点指向虚轴上iw点的矢量。
∣ L ( i w ) ∣ = K 1 ∏ j = 1 m N j / ∏ i = 1 n M i φ ( w ) = ∑ j = 1 m θ j − ∑ i = 1 i μ i left | L(iw)right | =K_1 prod_{j=1}^{m}N_j / prod_{i=1}^{n}M_i \ varphi(w) =sum_{j=1}^{m} theta _j-sum_{i=1}^{i} mu _i ∣L(iw)∣=K1j=1∏mNj/i=1∏nMiφ(w)=j=1∑mθj−i=1∑iμi
-
幅频特性:零点矢量模的乘积除以极点矢量模的乘积,再乘上暂态增益 K 1 K_1 K1
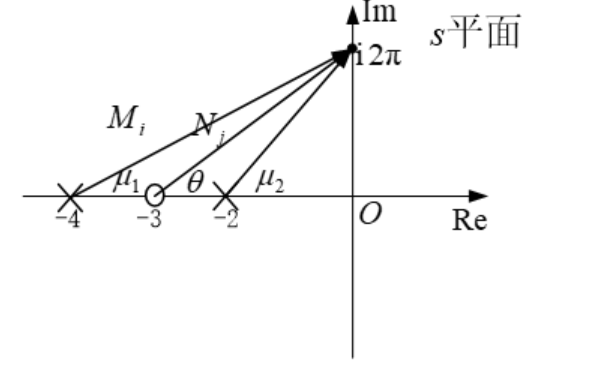
1.2.3 例子
画出频率特性G(iω)=(iω+3)/[(iω+2)(iω+4)]在频率为1Hz时的极点矢量和零点矢量,并计算该频率下的幅频与相频。

1.3 计算系统响应

2.开环频率特性幅相曲线
2.1 典型环节幅相曲线-Nyquist图

2.2一般特性频率曲线
2.2.1 开环传递函数:
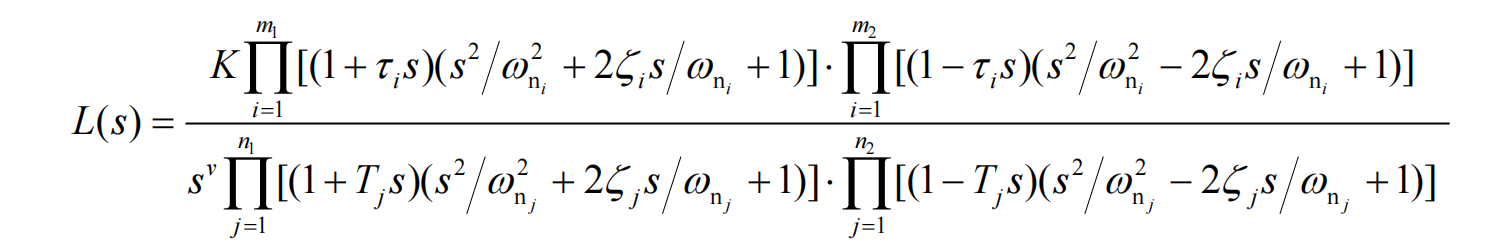
- 幅频:|L(iw)|
- 相频:
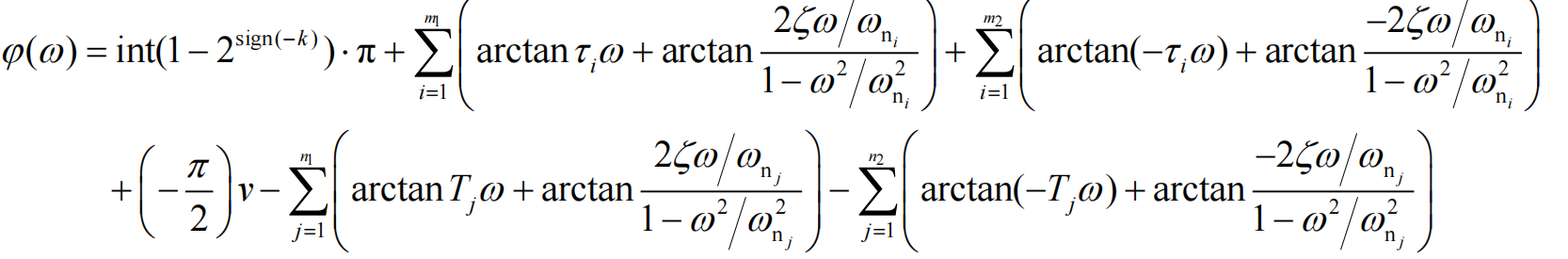
2.2.2 幅相曲线的绘制:
-
开环幅相曲线的起点(w= 0 + 0^+ 0+)和终点(w= ∞ infty ∞)
L ( i 0 + ) = { K e i 0 , ν = 0 ∞ e − i ν × 90 , ν > 0 L ( i ∞ ) = 0 e − i ( n − m ) 90 当 没 有 右 半 平 面 的 开 环 零 极 点 时 取 小 正 数 ϵ ∠ L ( i ϵ ) = − ν × 90 + ∑ arctan τ k ϵ − ∑ arctan T j ϵ ≈ − ν × 90 + ( ∑ τ k − ∑ T j ) ϵ L(i0^+)=left{begin{matrix} Ke^{i0}, quad nu =0\ infty e^{-inu times 90 },quad nu >0 end{matrix}right. \ L(iinfty )=0e^{-i(n-m)90} \ 当没有右半平面的开环零极点时\取小正数epsilon quad angle L(iepsilon )=-nu times 90+sum arctan tau_kepsilon -sum arctan T_jepsilon \ approx -nu times 90+(sum tau_k-sum T_j)epsilon L(i0+)={Kei0,ν=0∞e−iν×90,ν>0L(i∞)=0e−i(n−m)90当没有右半平面的开环零极点时取小正数ϵ∠L(iϵ)=−ν×90+∑arctanτkϵ−∑arctanTjϵ≈−ν×90+(∑τk−∑Tj)ϵ -
开环幅相曲线与负实轴的交点,交点坐标为:
R e L ( i w ) = L ( i w ) 令 虚 部 为 0 ReL(iw) = L(iw) quad 令虚部为0 ReL(iw)=L(iw)令虚部为0 -
开环幅相曲线的变化范围(象限性,单调性)
2.2.3 特征点
-
相位穿越频率:首次使得相位为-180°。
∠ L ( i w p c ) = − 180 ° angle L(iw_{pc})=-180° ∠L(iwpc)=−180° -
增益穿越频率 w c w_c wc:首次使得增益为1
∣ L ( i w c ) ∣ = 1 |L(iw_c)|=1 ∣L(iwc)∣=1
2.2.4 例子

3.开环对数频率特性
3.1Bode图概念
Bode图由对数幅频特性和相频特性构成。通常以分贝值作为纵坐标。
∣
L
(
i
w
)
∣
d
B
=
20
lg
∣
L
(
i
w
)
∣
(
d
B
)
|L(iw)|_{dB}=20lg^{|L(iw)|}(dB)
∣L(iw)∣dB=20lg∣L(iw)∣(dB)
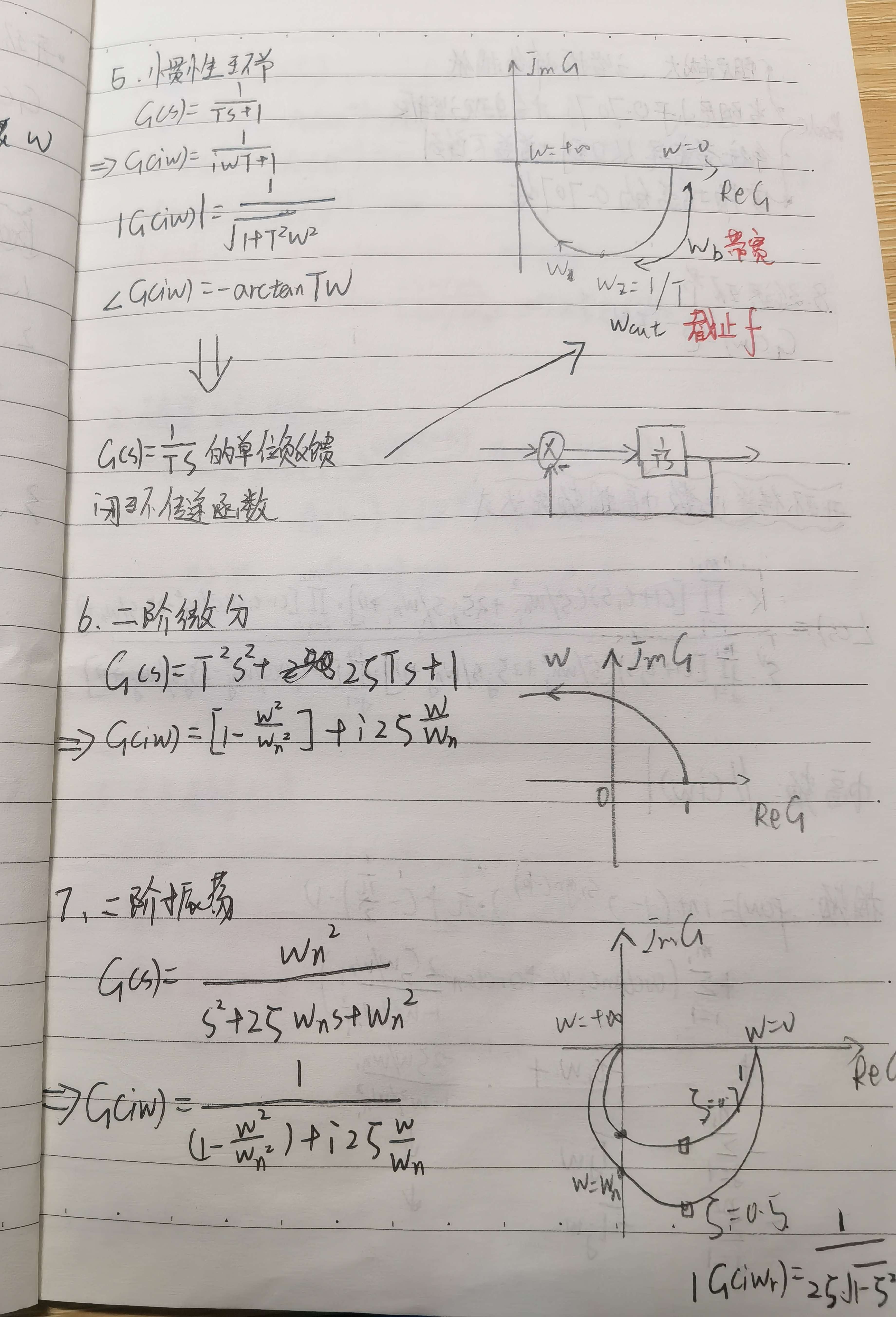
3.2 典型环节Bode图
-
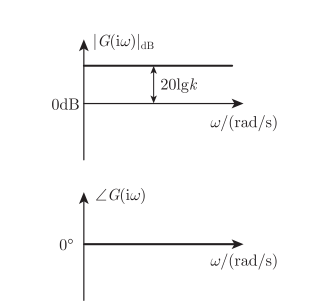
比例环节
频率特性为 ∣ G ( i w ) ∣ = k |G(iw)|=k ∣G(iw)∣=k
对数幅频特性: 20 lg ∣ G ( i w ) ∣ = 20 lg k 20lg{|G(iw)|}=20lg^k 20lg∣G(iw)∣=20lgk
相频特性: ∠ G ( i w ) = 0 ° angle G(iw)=0degree ∠G(iw)=0°
-
微分环节
G ( i w ) = i T d w G(iw)=iT_dw G(iw)=iTdw
对数幅频特性: 20 lg ∣ G ( i w ) ∣ = 20 lg T d w 20lg|G(iw)|=20lg{T_dw} 20lg∣G(iw)∣=20lgTdw
相频特性: ∠ G ( i w ) = 90 ° angle G(iw) = 90degree ∠G(iw)=90°

-
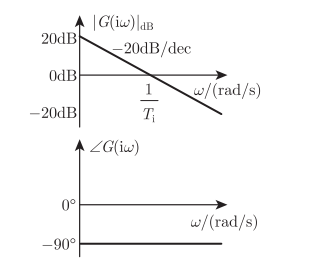
积分环节
G ( i w ) = 1 i T i w G(iw)=frac{1}{iT_iw} G(iw)=iTiw1
对数幅频特性: 20 l g ∣ G ( i w ) ∣ = − 20 lg ( T i w ) 20lg|G(iw)|=-20lg(T_iw) 20lg∣G(iw)∣=−20lg(Tiw)
相频特性: ∠ G ( i w ) = − 90 ° angle G(iw) =-90degree ∠G(iw)=−90°
-
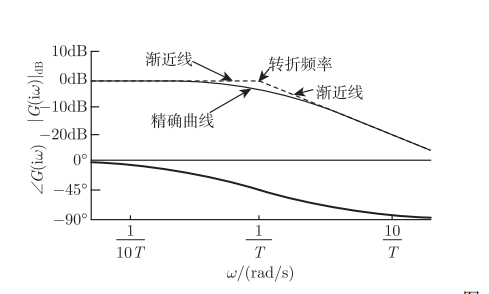
惯性环节
G ( i w ) = 1 i T w + 1 G(iw)=frac{1}{iTw+1} G(iw)=iTw+11
对数幅频特性: 20 l g ∣ G ( i w ) ∣ = − 10 lg [ 1 + ( w T ) 2 ] 20lg|G(iw)|=-10lg[1+(wT)^2] 20lg∣G(iw)∣=−10lg[1+(wT)2]
相频特性: ∠ G ( i w ) = − arctan w T angle G(iw)= -arctan wT ∠G(iw)=−arctanwT
-
一阶微分环节
G ( i w ) = 1 + i T w G(iw)=1+iTw G(iw)=1+iTw
对数幅频特性: 20 l g ∣ G ( i w ) ∣ = 10 lg [ 1 + ( w T ) 2 ] 20lg|G(iw)|=10lg[1+(wT)^2] 20lg∣G(iw)∣=10lg[1+(wT)2]
相频特性: ∠ G ( i w ) = arctan w T angle G(iw)=arctan wT ∠G(iw)=arctanwT
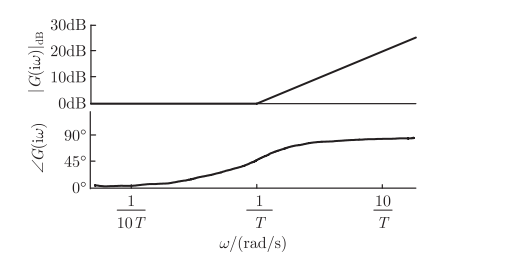
-
二阶振荡环节
G ( i w ) = 1 ( i T w ) 2 + 2 ζ i T w + 1 = 1 1 − ( w / w n ) 2 + i 2 ζ w / w n G(iw)=frac{1}{(iTw)^2+2zeta iTw+1}=frac{1}{1-(w/w_n)^2+i2zeta w/w_n} G(iw)=(iTw)2+2ζiTw+11=1−(w/wn)2+i2ζw/wn1
对数幅频特性: 20 l g ∣ G ( i w ) ∣ = − 10 lg { [ 1 − ( w / w n ) 2 ] 2 + ( 2 ζ w / w n ) 2 } 20lg|G(iw)|=-10lg {[1-(w/w_n)^2]^2+(2zeta w/w_n)^2} 20lg∣G(iw)∣=−10lg{[1−(w/wn)2]2+(2ζw/wn)2}
相频特性:
∠ G ( i w ) = { − arctan 2 ζ w / w n 1 − w 2 / w n 2 , w < w n − 180 ° − arctan 2 ζ w / w n 1 − w 2 / w n 2 , w > w n angle G(iw)=left {begin{matrix} -arctanfrac{2zeta w/w_n}{1-w^2/w_n^2},quad w<w_n \ -180degree -arctanfrac{2zeta w/w_n}{1-w^2/w_n^2},quad w>w_n \ end{matrix} right. ∠G(iw)={−arctan1−w2/wn22ζw/wn,w<wn−180°−arctan1−w2/wn22ζw/wn,w>wn
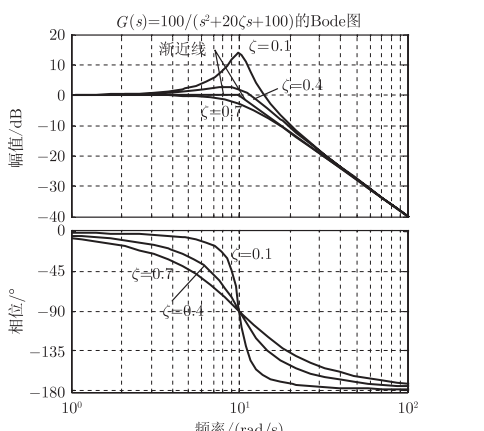
-
二阶微分环节
G ( i ω ) = 1 − ( ω / ω n ) 2 + i 2 ζ ω / ω n G(iω)=1−(ω/ω_n)^2+i2ζω/ω_n G(iω)=1−(ω/ωn)2+i2ζω/ωn
对数幅频特性: 20 l g ∣ G ( i w ) ∣ = 10 lg { [ 1 − ( ω / ω n ) 2 ] 2 + ( 2 ζ w / w n ) 2 20lg|G(iw)|=10 lg {[1−(ω/ω_n)^2]^2+(2zeta w/w_n)^2 20lg∣G(iw)∣=10lg{[1−(ω/ωn)2]2+(2ζw/wn)2
相频特性: ∠ G ( i w ) = { arctan 2 ζ w / w n 1 − w 2 / w n 2 , w < w n 180 ° + arctan 2 ζ w / w n 1 − w 2 / w n 2 , w > w n angle G(iw)=left {begin{matrix} arctanfrac{2zeta w/w_n}{1-w^2/w_n^2},quad w<w_n \ 180degree +arctanfrac{2zeta w/w_n}{1-w^2/w_n^2},quad w>w_n \ end{matrix} right. ∠G(iw)={arctan1−w2/wn22ζw/wn,w<wn180°+arctan1−w2/wn22ζw/wn,w>wn
-
延迟环节
G ( i w ) = e − i τ w G(iw)=e^{-itau w} G(iw)=e−iτw
对数幅频特性:$20lg|G(iw)|=0 $
相频特性: ∠ G ( i w ) = − τ w angle G(iw)=-tau w ∠G(iw)=−τw
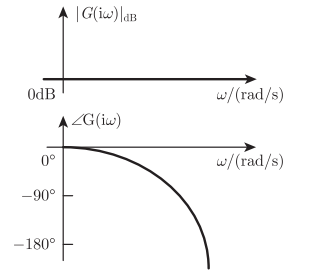
3.3 Bode图渐近线画法:
-
将开环传递函数写成时间常数标准式,确定系统开环增益K,把各典型环节的转折频率依次标在频率轴。
L ( s ) = K 1 ∏ j = 1 m ( s − z j ) ∏ i = 1 n ( s − p i ) L(s)=frac{K_1prod^m_{j=1}(s-z_j)}{prod^n_{i=1}(s-p_i)} L(s)=∏i=1n(s−pi)K1∏j=1m(s−zj) -
由于系统低频段渐近线的频率特性为 K / ( i w ) ν K/(iw)^nu K/(iw)ν,因此,过 ( K ν , 0 ) 或 ( 1 , 20 lg K ) (sqrt[nu]K,0)或(1,20lg K) (νK,0)或(1,20lgK)点绘制斜率为 − ν × 20 d B / d e c -nu times 20dB/dec −ν×20dB/dec的直线为低频段渐近线( ν 为 积 分 环 节 数 nu为积分环节数 ν为积分环节数)纯积分无转折频率
-
沿频率增大方向没遇到一个转折频率改变一次斜率,遇到分子一阶环节,频率+20dB/dec,二阶+40dB/dec,同理分母为负。渐近线最后一段斜率为-20(n-m)dB/dec.
-
绘制相频特性曲线,分别绘制各环节相频曲线,最后进行叠加
3.4最小相位系统:
最小相位系统:没有开环RHP1零点和极点的系统。
非最小相位系统:含有开环RHP零点、极点,其相位滞后较大
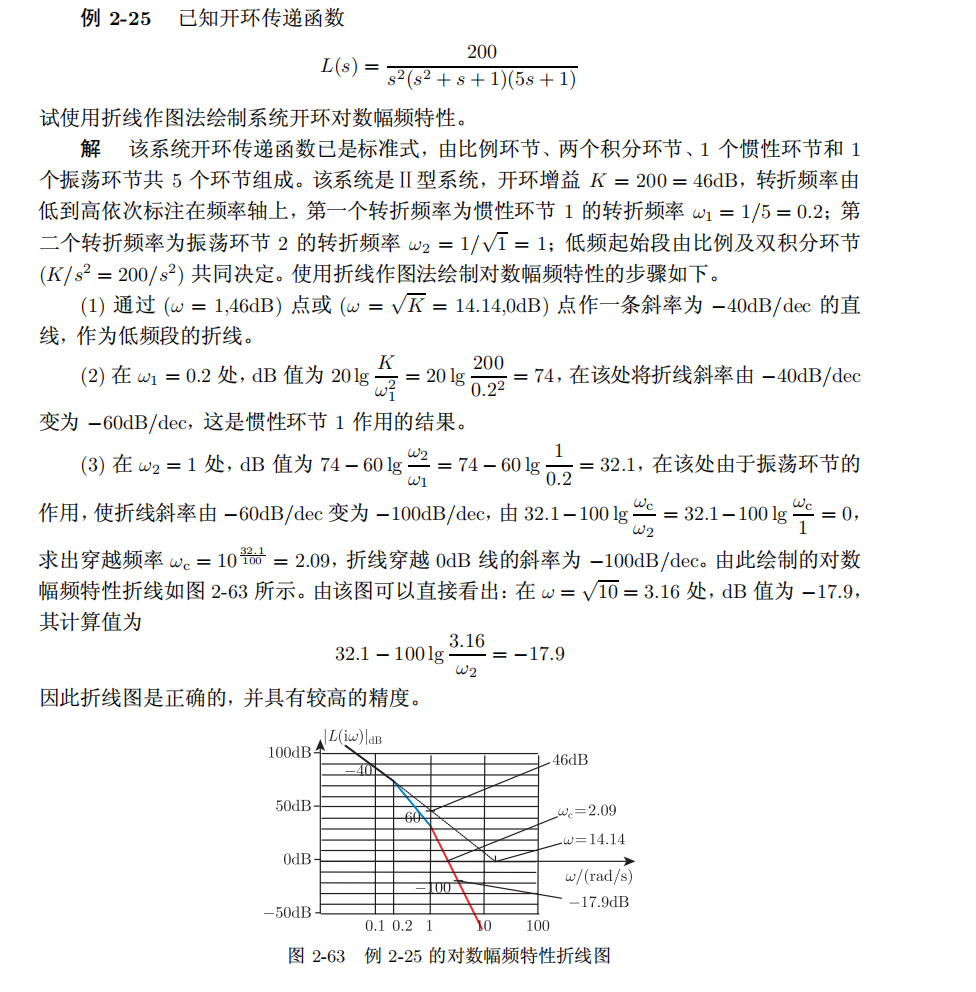
3.5举例
Right Half Plane ↩︎
最后
以上就是烂漫蜡烛最近收集整理的关于自控原理学习笔记-反馈控制系统的动态模型(4)-频率特性函数Nyquist图及Bode图1.频率特性函数2.开环频率特性幅相曲线3.开环对数频率特性的全部内容,更多相关自控原理学习笔记-反馈控制系统内容请搜索靠谱客的其他文章。








发表评论 取消回复