概述
无意间在知乎上看到某篇文章，关于奈奎斯特定理的，很生动形象的解释了定理含义；可以简单的理解为：当采样频率大于信号中最高频率的2倍时(fs>2f)，采样之后的数字信号完整地保留了原始信号中的信息。奈奎斯特定理又被成为采样定理。
我们可以用一个旋转轮来形象理解这个定理，
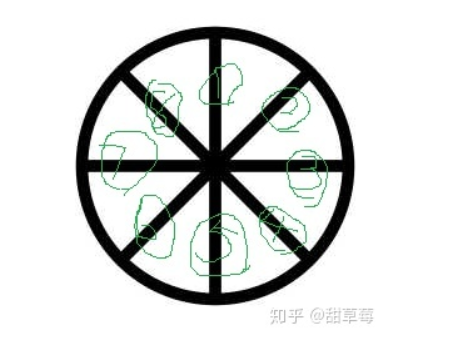
这是一个各个轴之间间隔45度的轮子，每个轮子都被标上了标识。
假设这个轮子以每秒45度来转动，那么每个轴返回原位需要8秒（采样周期）。
那么如果我们每8,16,24秒来用相机拍照，是不是每次都可以拍摄到原图像静止不动？
这是因为在采样周期内，车轮旋转的整数周期都会回到原位，不论旋转方向如何。那么就有了一个非常重要的结论：
采样周期的整数倍不能检测到相位（状态）变化。
我们来减少一点拍摄周期，如果以每4秒的速度拍摄呢？
每4秒拍照一次，轮子只能转一半，那么我们可以在照片中检测到轮子正在旋转，虽然依然不能区分它的旋转方向，但是轮子的状态（相位）已经可以区分了。
那么再减少一点拍摄周期，以每3秒的速度拍摄呢？
无论顺时针还是逆时针，都可以看到轮轴的错位（相位的变化）。
这就是Nyquist-Shannon采样定理，我们希望同时看到轮子的旋转和相位变化，采样周期要小于整数周期的1/2，采样频率应该大于原始频率的2倍。同理，对于模拟信号，我们希望同时看到信号的各种特性，采样频率应该大于原始模拟信号的最大频率的两倍，否则将发生混叠（相位/频率模糊）。
最后
以上就是怕孤独衬衫为你收集整理的如何理解奈奎斯特定律？的全部内容，希望文章能够帮你解决如何理解奈奎斯特定律？所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
发表评论 取消回复