频域分析及奈氏判据
- 频域分析及奈氏判据
- 1. 频域分析
- 2. 幅相频率特性(Nyquist图)
- 3. 对数频率特性(Bode图)
- 4. 频域稳定判据
- 5. 奈氏判据例题
- 6. 再来奈氏判据
- 0型系统
- I 型系统或 II 型系统
- 简化奈奎斯特稳定判据
- 1. ω omega ω 由 0 0 0 变化到 + ∞ +infty +∞ 时的开环幅相频率特性 G K ( j ω ) G_K(jomega) GK(jω)
- 2. 采用穿越的概念简化复杂曲线包围次数的计算
- 3.半次穿越
- 4. 型别 ν ≥ 1 nu ge1 ν≥1 系统开环频率特性 G K ( j ω ) G_K(jomega) GK(jω) 曲线的处理
频域分析及奈氏判据
1. 频域分析
幅频特性:幅值之比
相频特性:相角之差
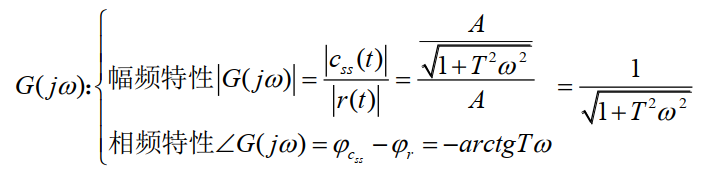
2. 幅相频率特性(Nyquist图)
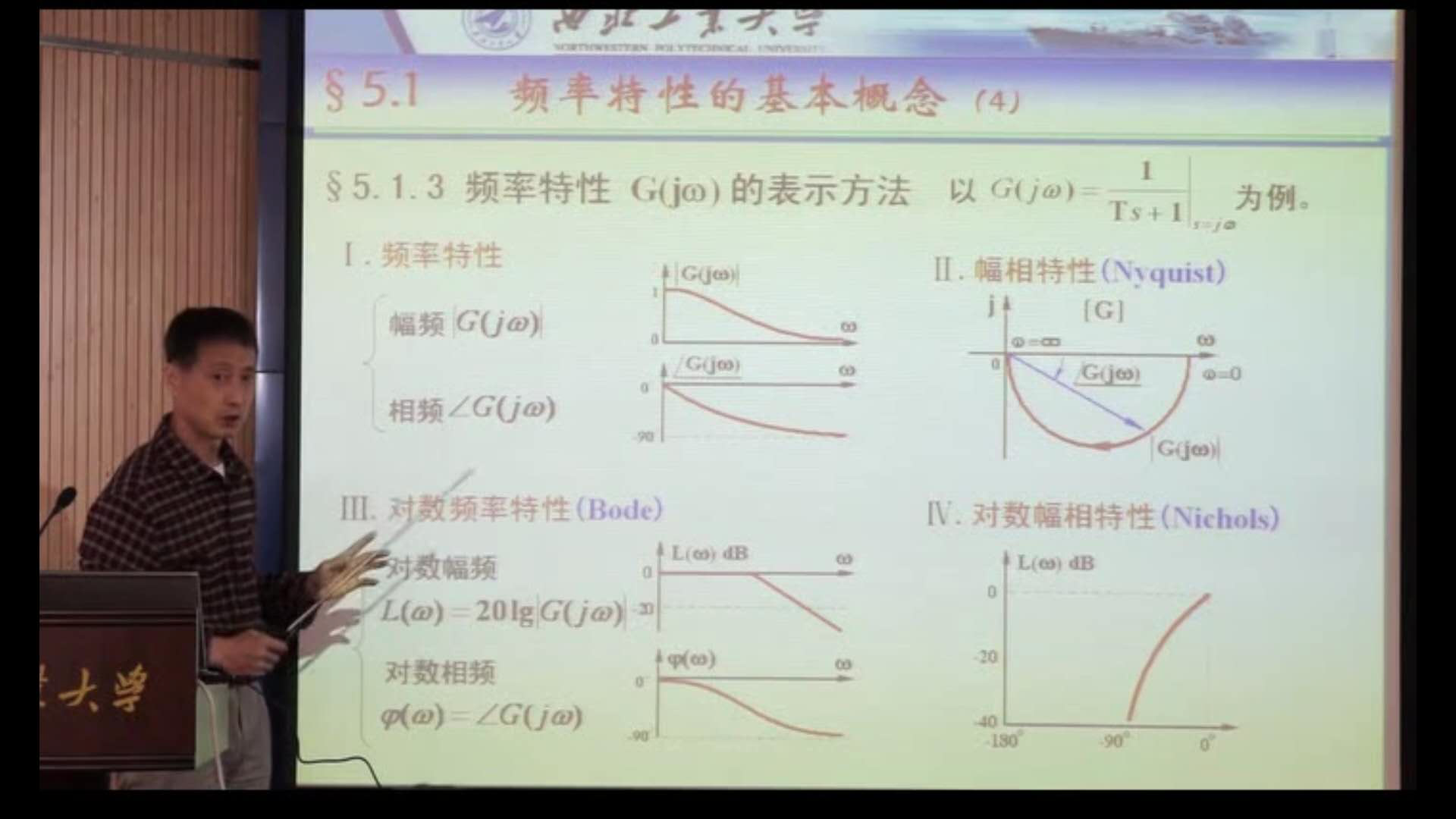
From: 自动控制原理(西北工业大学 卢京潮)-P33
3. 对数频率特性(Bode图)
4. 频域稳定判据

From: 自动控制原理(西北工业大学 卢京潮)-P40

From: 自动控制原理(西北工业大学 卢京潮)-P42

5. 奈氏判据例题
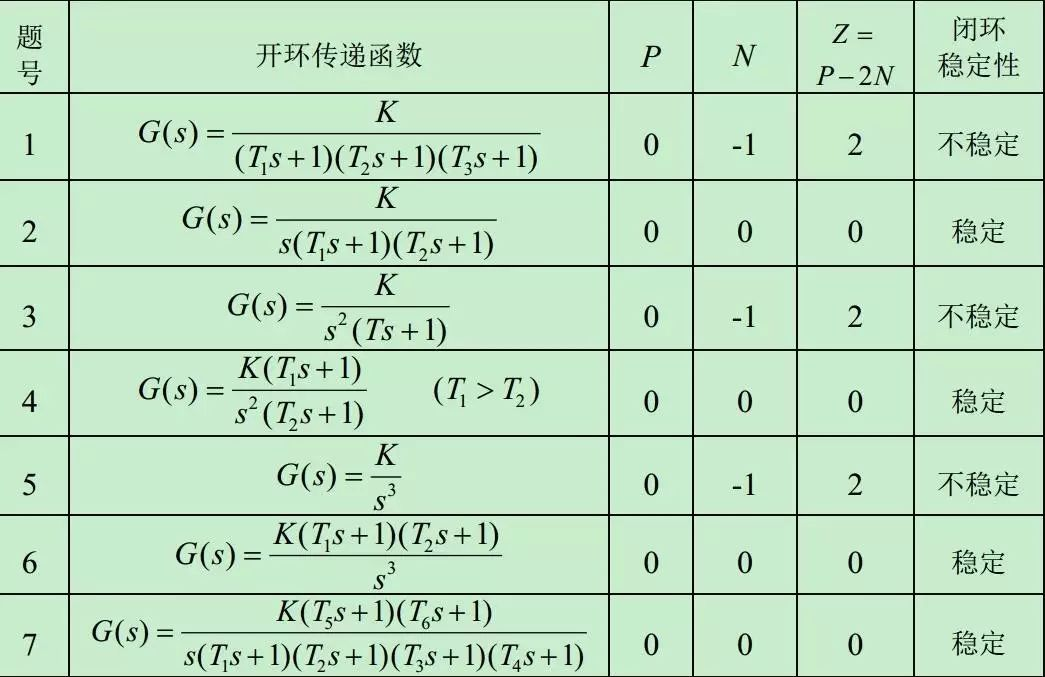
例题:试根据奈奎斯特判据,判断下表所示曲线对应闭环系统的稳定性,已知曲线(1)~(10)对应的开环传递函数如下:
| 题号 | 传函 |
|---|---|
| (1) | G ( s ) = K ( T 1 s + 1 ) ( T 2 s + 1 ) ( T 3 s + 1 ) G(s) = frac{K}{(T_1 s+1)(T_2 s+1)(T_3 s+1)} G(s)=(T1s+1)(T2s+1)(T3s+1)K |
| (2) | G ( s ) = K s ( T 1 s + 1 ) ( T 2 s + 1 ) G(s) = frac{K}{s(T_1 s+1)(T_2 s+1)} G(s)=s(T1s+1)(T2s+1)K |
| (3) | G ( s ) = K s 2 ( T s + 1 ) G(s) = frac{K}{s^2 (T_ s+1)} G(s)=s2(Ts+1)K |
| (4) | G ( s ) = K ( T 1 s + 1 ) s 2 ( T 2 s + 1 ) , ( T 1 > T 2 ) G(s) = frac{K (T_1s+1)}{s^2 (T_2 s+1)},quad(T_1>T_2) G(s)=s2(T2s+1)K(T1s+1),(T1>T2) |
| (5) | G ( s ) = K s 3 G(s) = frac{K}{s^3} G(s)=s3K |
| (6) | G ( s ) = K ( T 1 s + 1 ) ( T 2 s + 1 ) s 3 G(s) = frac{K(T_1s+1)(T_2s+1)}{s^3} G(s)=s3K(T1s+1)(T2s+1) |
| (7) | G ( s ) = K ( T 5 s + 1 ) ( T 6 s + 1 ) s ( T 1 s + 1 ) ( T 2 s + 1 ) ( T 3 s + 1 ) ( T 4 s + 1 ) G(s) = frac{K(T_5s+1)(T_6s+1)}{s(T_1s+1)(T_2s+1)(T_3s+1)(T_4s+1)} G(s)=s(T1s+1)(T2s+1)(T3s+1)(T4s+1)K(T5s+1)(T6s+1) |
| (8) | G ( s ) = K T 1 s − 1 ( K > 1 ) G(s) = frac{K}{T_1s-1}quad(K>1) G(s)=T1s−1K(K>1) |
| (9) | G ( s ) = K T 1 s − 1 ( K < 1 ) G(s) = frac{K}{T_1s-1}quad(K<1) G(s)=T1s−1K(K<1) |
| (10) | G ( s ) = K s ( T s − 1 ) G(s) = frac{K}{s(Ts-1)} G(s)=s(Ts−1)K |
答案如下:
| 题号 | 传函 | P P P | N N N | Z = P − 2 N Z=P-2N Z=P−2N | 闭环稳定性 |
|---|---|---|---|---|---|
| (1) | G ( s ) = K ( T 1 s + 1 ) ( T 2 s + 1 ) ( T 3 s + 1 ) G(s) = frac{K}{(T_1 s+1)(T_2 s+1)(T_3 s+1)} G(s)=(T1s+1)(T2s+1)(T3s+1)K | 0 | -1 | 2 | 不稳定 |
| (2) | G ( s ) = K s ( T 1 s + 1 ) ( T 2 s + 1 ) G(s) = frac{K}{s(T_1 s+1)(T_2 s+1)} G(s)=s(T1s+1)(T2s+1)K | 0 | 0 | 0 | 稳定 |
| (3) | G ( s ) = K s 2 ( T s + 1 ) G(s) = frac{K}{s^2 (T_ s+1)} G(s)=s2(Ts+1)K | ||||
| (4) | G ( s ) = K ( T 1 s + 1 ) s 2 ( T 2 s + 1 ) , ( T 1 > T 2 ) G(s) = frac{K (T_1s+1)}{s^2 (T_2 s+1)},quad(T_1>T_2) G(s)=s2(T2s+1)K(T1s+1),(T1>T2) | ||||
| (5) | G ( s ) = K s 3 G(s) = frac{K}{s^3} G(s)=s3K | ||||
| (6) | G ( s ) = K ( T 1 s + 1 ) ( T 2 s + 1 ) s 3 G(s) = frac{K(T_1s+1)(T_2s+1)}{s^3} G(s)=s3K(T1s+1)(T2s+1) | ||||
| (7) | G ( s ) = K ( T 5 s + 1 ) ( T 6 s + 1 ) s ( T 1 s + 1 ) ( T 2 s + 1 ) ( T 3 s + 1 ) ( T 4 s + 1 ) G(s) = frac{K(T_5s+1)(T_6s+1)}{s(T_1s+1)(T_2s+1)(T_3s+1)(T_4s+1)} G(s)=s(T1s+1)(T2s+1)(T3s+1)(T4s+1)K(T5s+1)(T6s+1) | ||||
| (8) | G ( s ) = K T 1 s − 1 ( K > 1 ) G(s) = frac{K}{T_1s-1}quad(K>1) G(s)=T1s−1K(K>1) | ||||
| (9) | G ( s ) = K T 1 s − 1 ( K < 1 ) G(s) = frac{K}{T_1s-1}quad(K<1) G(s)=T1s−1K(K<1) | ||||
| (10) | G ( s ) = K s ( T s − 1 ) G(s) = frac{K}{s(Ts-1)} G(s)=s(Ts−1)K |
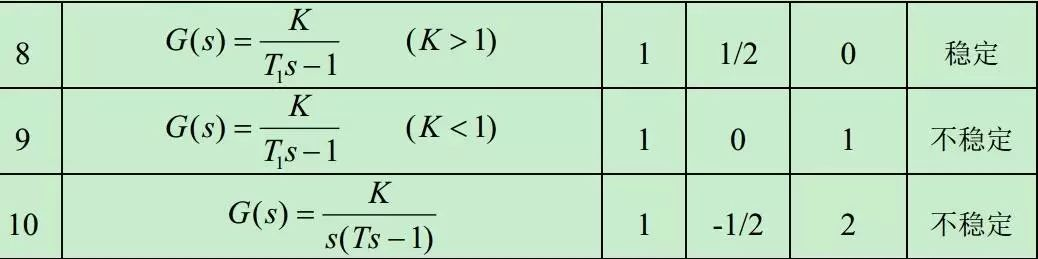
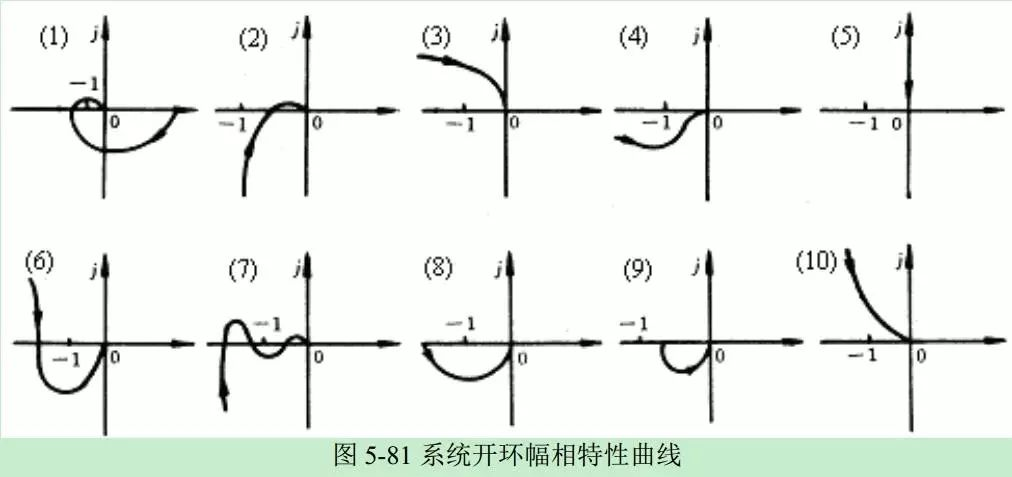
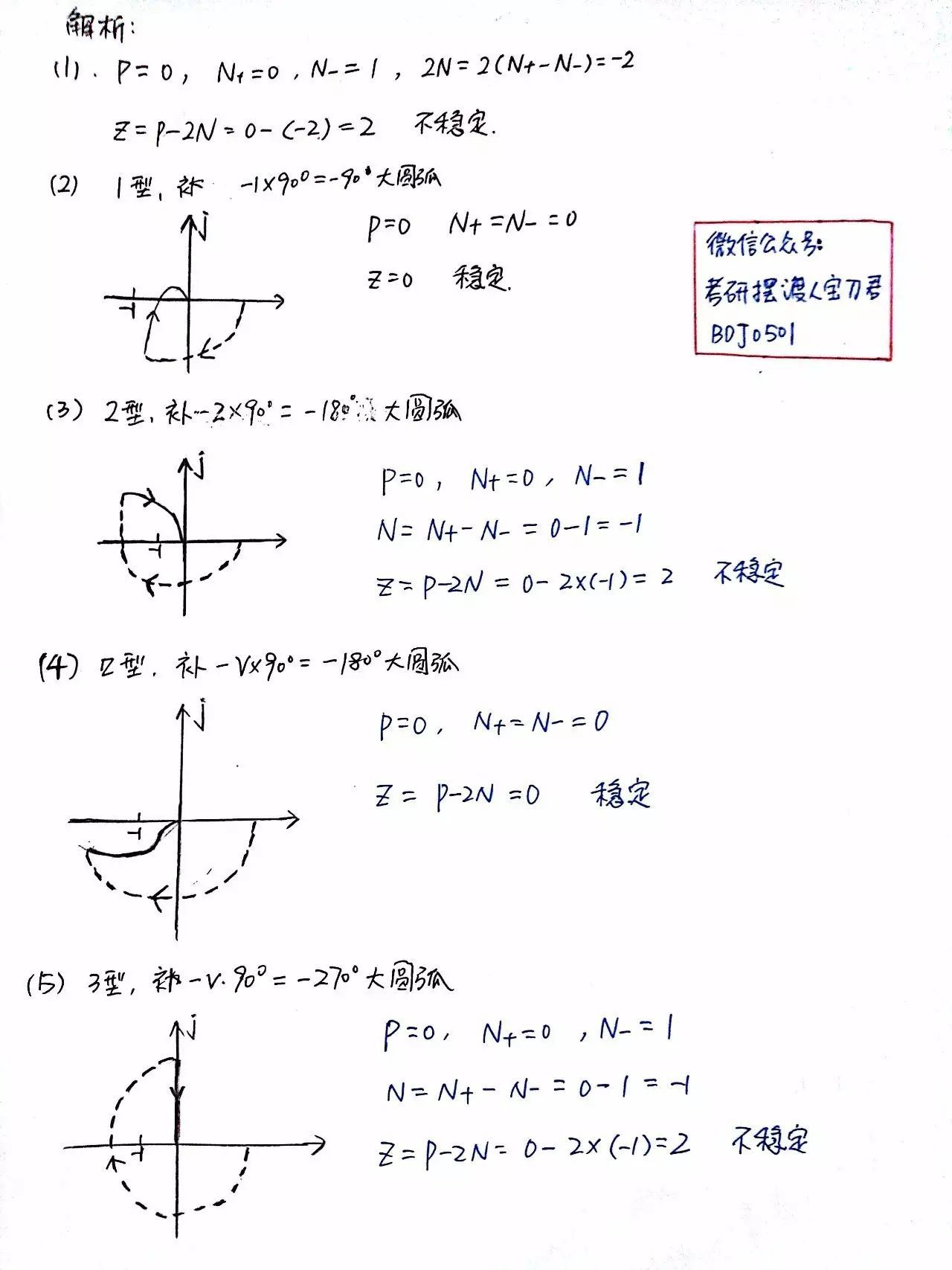
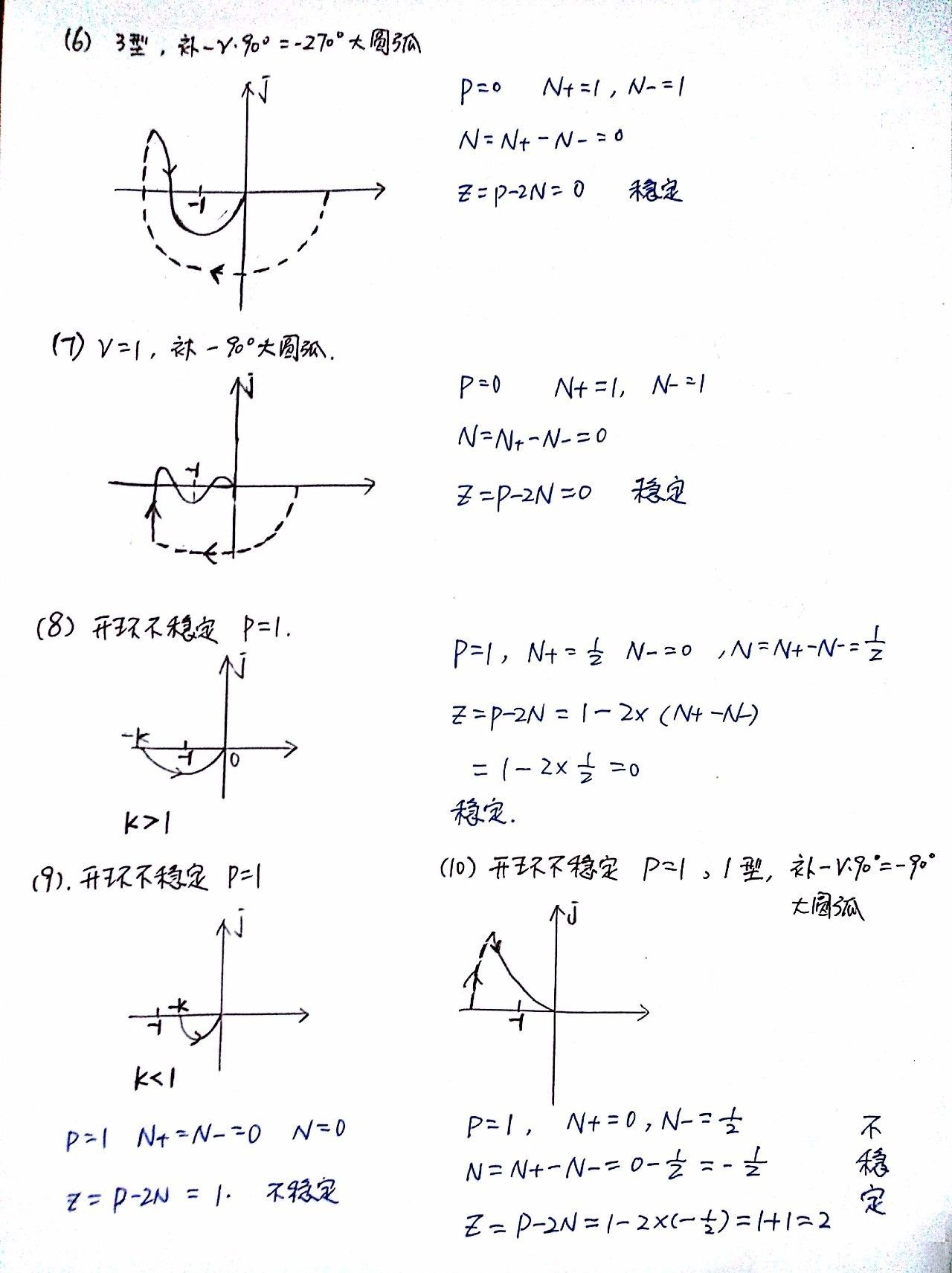
From: 真开心!奈奎斯特稳定判据,我终于掌握了!
6. 再来奈氏判据
系统稳定的充要条件是系统闭环特征根都具有复实部,即都在 s s s 复平面的左边平面 (LHP)。
在时域分析中判断系统的稳定性,一种方法是求出特征方程的全部根,另一种方法是使用劳斯-胡尔维茨稳定判据(代数判据)。然而,这两种方法都有不足之处,对于高阶系统,非常困难且费时,也不便于研究系统参数、结构对稳定性的影响。
特别是,如果知道了开环特性,要研究闭环系统的稳定性,还需要求出闭环特征方程,无法直接利用开环特性判断闭环系统的稳定性。而对于一个自动控制系统,其开环数学模型易于获取,同时它包含了闭环系统所有环节的动态结构和参数。
除了劳斯判据外,分析系统稳定性的另一个常用判据为奈奎斯特(Nyquist)判据。Nyquist稳定判据是奈奎斯特于1932年提出的,是频率法的重要内容,简称奈氏判据。
奈氏判据的主要特点有:
- 根据系统的开环频率特性,来研究闭环系统稳定性,而不必求闭环特征根;
- 能够确定系统的稳定程度(想对稳定性);
- 可用于分析系统的瞬态性能,利于对系统的分析于设计;
- 基于系统的开环奈氏图,是一种图解法。
Nyquist判据的主要理论依据是复变函数理论中的Cauch(柯西)幅角定理。
0型系统
系统的开环右极点数为 P P P,在 G ( s ) H ( s ) G(s)H(s) G(s)H(s) 平面上,当 ω omega ω 从 − ∞ -infty −∞ 变化到 + ∞ +infty +∞ 时,系统开环频率特性曲线 G ( j ω ) H ( j ω ) G(jomega)H(jomega) G(jω)H(jω) 及其镜像,顺时针包围 ( − 1 , j 0 ) (-1,j0) (−1,j0) 点的次数为 N N N 圈 ( N > 0 ) (N>0) (N>0),若逆时针包围则 N < 0 N<0 N<0,封闭曲线绕 ( − 1 , j 0 (-1,j0 (−1,j0 点旋转 36 0 ∘ 360^circ 360∘ 即包围一次,则系统的闭环右极点的个数为 Z Z Z,且满足: Z = N + P Z=N+P Z=N+P
当
Z
=
0
Z=0
Z=0 时,系统闭环稳定;
当
Z
>
0
Z>0
Z>0 时,系统闭环不稳定。
注:系统开环稳定,闭环不一定稳定;开环不稳定,闭环不一定不稳定。
I 型系统或 II 型系统
I 型系统:从正虚轴方向无限远处开始,顺时针绕向负虚轴,以原点为圆心,半径为无限大的右半圆弧。需在 G ( s ) H ( s ) G(s)H(s) G(s)H(s) 平面上补画右半圆弧将奈氏曲线及其镜像连成封闭曲线。
II 型系统:从负实轴方向无限远处开始,顺时针绕一周终止于负实轴方向,以原点为圆心,半径为无限大的圆弧。需在 G ( s ) H ( s ) G(s)H(s) G(s)H(s) 平面上补画整圆将奈氏曲线及其镜像连成封闭曲线。
当系统的开环奈氏图作如上处理后,稳定判据与 0 型系统完全相同。
若系统为最小相位系统,即开环系统稳定时 ( P = 0 ) (P=0) (P=0),系统稳定的充要条件为:当 ω omega ω 从 − ∞ -infty −∞ 变化到 + ∞ +infty +∞ 时,在 G H GH GH 平面上的系统开环频率特性曲线及其镜像,不包围 ( − 1 , j 0 ) (-1,j0) (−1,j0) 点,即 N = 0 N=0 N=0,则 Z = N + P = 0 Z=N+P=0 Z=N+P=0,闭环系统稳定;否则不稳定。
当系统开环频率特性曲线及其镜像通过 ( − 1 , j 0 ) (-1,j0) (−1,j0) 点时,表明在 s s s 平面虚轴上有闭环极点,系统处于临界稳定状态,属于不稳定。
简化奈奎斯特稳定判据
1. ω omega ω 由 0 0 0 变化到 + ∞ +infty +∞ 时的开环幅相频率特性 G K ( j ω ) G_K(jomega) GK(jω)
因为 ( 0 , + ∞ ) (0, +infty) (0,+∞) 与 ( 0 , − ∞ ) (0, -infty) (0,−∞) 的曲线完全关于实轴对称,则 0 0 0 变到 + ∞ +infty +∞ 时的开环幅相频率特性 G K ( j ω ) G_K(jomega) GK(jω) 顺时针包围 ( − 1 , j 0 ) (-1,j0) (−1,j0) 点的圈数 N ′ N' N′ 满足: N ′ = N / 2 N' = N/2 N′=N/2
已知系统开环右极点个数为 P P P,则系统闭环右极点个数为 Z Z Z(不包括虚轴上的极点): Z = P + 2 N ′ Z = P+2N' Z=P+2N′
2. 采用穿越的概念简化复杂曲线包围次数的计算
ω
omega
ω 由
0
0
0 变化到
+
∞
+infty
+∞ 时开环频率特性曲线要形成对
(
−
1
,
j
0
)
(-1, j0)
(−1,j0) 点的一次包围,势必穿越
(
−
∞
,
−
1
)
(-infty, -1)
(−∞,−1) 区间一次。
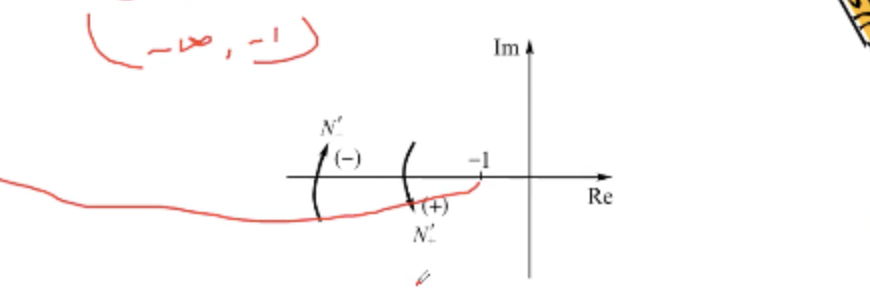
开环频率特性曲线逆时针穿越
(
−
∞
,
−
1
)
(-infty, -1)
(−∞,−1) 区间时,随
ω
omega
ω 增加,频率特性的相角值增大,称为一次 正穿越
N
+
′
N'_+
N+′。反之,
开环频率特性曲线顺时针穿越
(
−
∞
,
−
1
)
(-infty, -1)
(−∞,−1) 区间时,随
ω
omega
ω 增加,频率特性的相角值减小,称为一次 负穿越
N
−
′
N'_-
N−′。
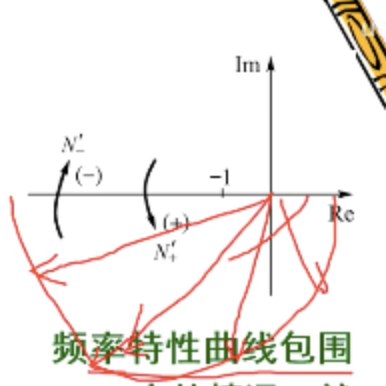
频率特性曲线包围
(
−
1
,
j
0
)
(-1,j0)
(−1,j0) 点的情况,就可以利用频率特性曲线在负实轴
(
−
∞
,
−
1
)
(-infty, -1)
(−∞,−1) 区间的正、负穿越来表达。
ω omega ω 由 0 0 0 变到 + ∞ +infty +∞ 时的开环幅相频率特性 G K ( j ω ) G_K(jomega) GK(jω) 对 ( − 1 , j 0 ) (-1,j0) (−1,j0) 点的总包围次数为 N ′ = ( N − ′ − N + ′ ) N'=(N'_- - N'_+) N′=(N−′−N+′)
利用正负穿越情况的奈奎斯特稳定判据叙述为: Z = P + 2 ( N − ′ − N + ′ ) Z = P+2(N'_- - N'_+) Z=P+2(N−′−N+′)
注:奈氏曲线在 ( − 1 , j 0 ) (-1,j0) (−1,j0) 点以右负实轴上相位有变化不算穿越。
3.半次穿越
奈氏曲线始于或止于
(
−
1
,
j
0
)
(-1,j0)
(−1,j0) 点以左负实轴,称为一个半次穿越。
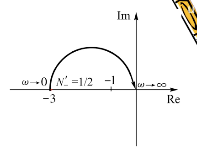
例题:某系统开环传递函数如下,试判断闭环系统的稳定性。
G
(
s
)
H
(
s
)
=
−
3
s
+
1
G(s)H(s) = frac{-3}{s+1}
G(s)H(s)=s+1−3
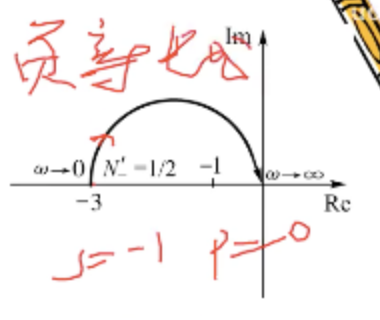
答:由于曲线始于
(
−
3
,
j
0
)
(-3,j0)
(−3,j0) 点,故顺时针包围
(
−
1
,
j
0
)
(-1, j0)
(−1,j0) 点的次数为 1/2,
N
−
′
=
1
2
N'_- =frac{1}{2}
N−′=21。由于开环右极点数为
P
=
0
P=0
P=0,故
Z
=
P
+
2
(
N
−
′
−
N
+
′
)
=
0
+
2
(
1
2
−
0
)
=
1
Z = P+2(N'_- - N'_+) = 0+2(frac{1}{2}-0) = 1
Z=P+2(N−′−N+′)=0+2(21−0)=1
闭环系统有一个右极点,闭环不稳定。
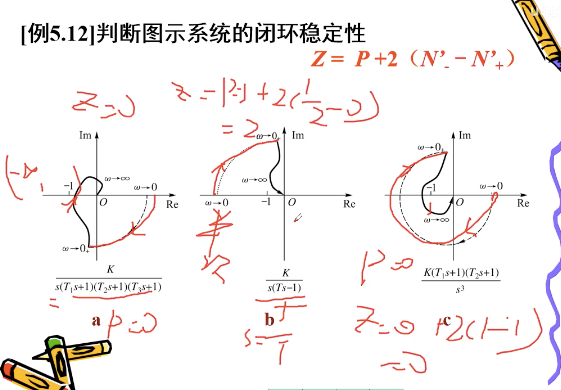
例题:经实验测得某最小相位系统的开环奈氏图如下所示,判断闭环稳定性。
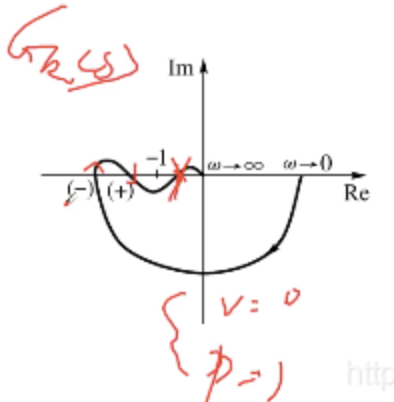
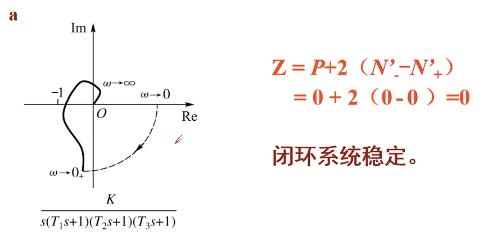
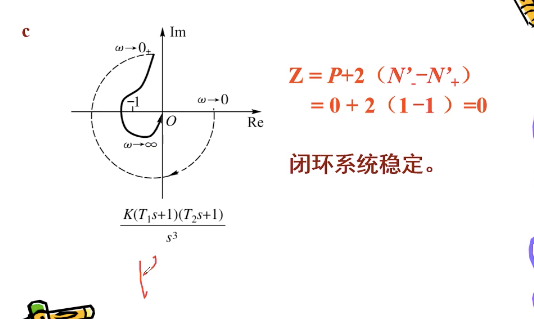
答:由于题意已告知时最小相位系统,而最小相位系统是稳定的,故可知 P = 0 P=0 P=0,且型别为 0 0 0,故直接利用开环频率特性 G K ( j ω ) G_K(jomega) GK(jω) 的轨迹曲线判断系统稳定性。由图可知,奈氏曲线由 ω = 0 omega=0 ω=0 到 ω = + ∞ omega=+infty ω=+∞ 先顺时针穿越区间 ( − ∞ , − 1 ) (-infty, -1) (−∞,−1) 一次,故 N − ′ = 1 N'_- = 1 N−′=1,后逆时针穿越一次,故 B + ′ = 1 B'_+ = 1 B+′=1。因此,利用公式有 Z = P + 2 ( N − ′ − N + ′ ) = 0 + 2 ( 1 − 1 ) = 0 Z = P + 2(N'_- - N'_+) = 0 + 2(1-1) = 0 Z=P+2(N−′−N+′)=0+2(1−1)=0
故由奈氏稳定判据知该闭环系统是稳定的。
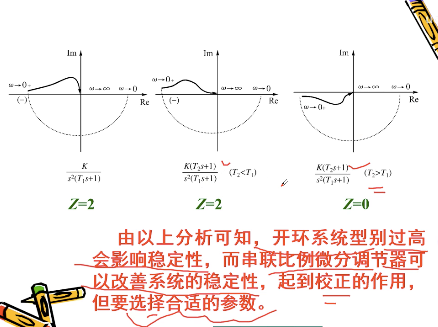
4. 型别 ν ≥ 1 nu ge1 ν≥1 系统开环频率特性 G K ( j ω ) G_K(jomega) GK(jω) 曲线的处理
在 ω = 0 omega=0 ω=0 附近,幅相特性以 ∞ infty ∞ 为半径,逆时针补画 θ = ν ⋅ 9 0 ∘ theta=nucdot 90^circ θ=ν⋅90∘ 的圆弧,添加圆弧后相当于得到新的开环频率特性 G K ( j ω ) G_K(jomega) GK(jω) 的曲线。
此圆弧与实轴或虚轴的交点相当于新的起点,对应 ω = 0 omega=0 ω=0,原有曲线的起点对应于 ω = 0 + omega=0^+ ω=0+。注意所指曲线仍为 ω omega ω 由 0 0 0 变到 + ∞ +infty +∞ 时的开环幅相频率特性 G K ( j ω ) G_K(jomega) GK(jω)。
当系统的开环奈氏曲线作以上处理后,带入简化奈氏稳定判据即可,且系统在虚轴上的 0 0 0 值开环极点作左极点处理。 Z = P + 2 ( N − ′ − N + ′ ) Z = P+2(N'_- - N'_+) Z=P+2(N−′−N+′)

From: 自控19奈氏判据
最后
以上就是甜蜜铅笔最近收集整理的关于【控制】频域分析及奈氏判据频域分析及奈氏判据的全部内容,更多相关【控制】频域分析及奈氏判据频域分析及奈氏判据内容请搜索靠谱客的其他文章。








发表评论 取消回复