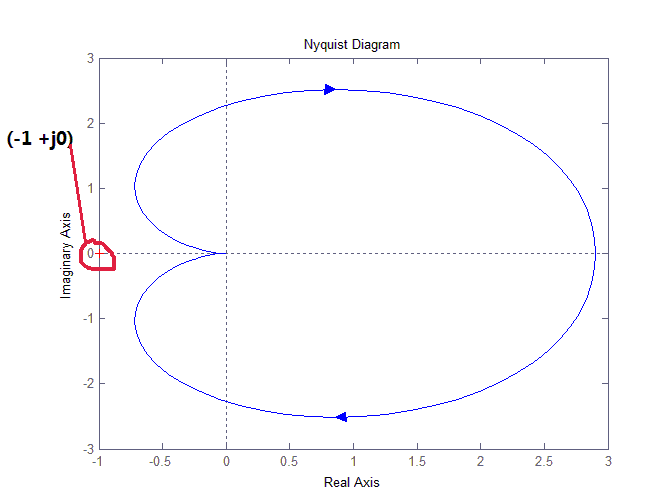
这是我去年5月份写的一个学习笔记。在控制或电源领域,一直存在在着两大派之争,一派是学者(理论派),数学功底厉害牛逼,他们毫不犹豫地用微积分得出BOOST拓扑的传递函数,然后出版写满公式的教科书。另一派则是电源或控制的专业人员,他们实践工作多年(实践派),具有深厚项目工程经验,但是很少见这样的工程师写书,也许是工作太忙或者别的原因。实践派认为那些抽象公式和理论对设计更好的电源产品根本起不了多大作用。而理论派则认为,没有数学公式的分析,你是不可能设计出优秀的高效的产品的。这到底是谁有道理啊,我觉得这两派折中一下。
对于学生或老师而言,多动手多实践;对于工作了的人,你想再提升一个高度的话,要注重基础理论的学习。这好比练武一样,你既要进行外功的练习,打桩、马步、力量,又要进行内功的练习,拳术套路技法,甚至内功心法、兵法等等。好了废话说了不少了,我们马上就要开始进入正题,学习内功心法了,哈哈。
下面讲的是经典控制理论中的奈奎斯特稳定判据(奈氏判据),发现很多考研的同学对奈氏判据感觉很难,很多教材还不统一,比如奈氏判据定义。
胡寿松版定义:反馈控制系统稳定充分的必要条件是半闭合曲线不穿过(-1,j0)点,且逆时针包围临界点(-1,j0)点圈数R等于开环转到函数的正实部极点数P。有幅角原理可知,闭合曲线包围函数F(S)= 1+ G(s)*H(s)的零点数即反馈控制系统正实部极点数为Z=P-R=P-2N
李红星版定义: 当ω从
(-1,+j)点N次,则Z=N+P…下面还有一大段就不抄了。
初一看,这两个概念怎么不一样啊,是不是某书错了?李的N等于胡的R,都表示一周的意思。所以李翻译成胡的是Z=R+P,胡是Z=P-R,这也差太多了吧。
其实都没有错,最终意思都一样的!区别在于:胡是半闭合曲线,逆时针包围(-1,j0)点,
Z=P-R。李是全闭合曲线, 顺时针包围(-1,+j0)点, Z=R+P。
看了上面两个定义,你理解了吗?是不是还是一头雾水?其实这些概念都是浓缩的精华,给已懂了的人看的,原来不懂的,看了还是不懂的,哈哈。要理解这句话,你必须把前面讲的内容全部看了并都理解,这有点难度,但其实也没有那么复杂,就是概念有点多,如果用matlab去做的话,真的是不要太简单哦。
上面定义的精华:右半平面是不能有闭环极点的,也就是Z=0,这个闭环极点就是F(S)零点,也是胡版描述的反馈控制系统的正实部极点数。我知道某些同学看到这里还是没有懂,那就进入下面的笔记吧。
下面你将学习的内容:
1 频率特性
2 奈奎斯特图
3 幅角原理
4 辅助函数
5 奈奎斯特稳定判据
6 matlab 命令窗口实验:奈氏曲线稳定判断的仿真
7 simulink 仿真实验:传递函数的阶跃响应的仿真
在控制系统的频域分析中,有两大法宝,分别是奈奎斯特稳定判据和对数频率稳定判据,它们本属同根,都有个共同名字叫频域稳定判据,都有个共同优点,能根据开环系统的频率特性曲线判定闭环系统的稳定性,本文介绍奈奎斯特稳定判据的基本原理,写本文的目的主要是巩固下自己学习的内容,并同时也算分享给一些正在学习这门课的学生参考,并能理解这一概念,从而在控制系统中能分析或使用这一个理论。本文档参考教材《自动控制原理》胡寿松版、《自动控制原理》李红星版、《西北工业大学自控教案》卢京潮教授。
其学习路线图如下,1 频率特性 ---> 2 奈奎斯特图 --> 3 幅角原理 --> 4 辅助函数--> 5 奈奎斯特稳定判据,前面4个环节搞通,最后一个原理也搞通了。
▲ 频率特性
那么什么是电路的频率特性呢?下面以RC电路为例,对什么是频率特性做一些解释:要研究一个电路方法有多种,一般我们知道某个电路的数学模型,给定一个信号,然后能求出输出或者叫响应。但是我们研究的是电路频率特性,所以我们输入要求是正弦信号,这个输出信号一般指的是稳态分量,瞬态分量随着时间趋向0了,(这个不理解的同学自己看书,这里不详细说了)。注意下面这段话很重要:其实我们暂时也不用管它是什么输出了,我们只要知道这个输出信号的幅度与相位会随着输入信号的频率的变化而变化,这就是频率特性了,它包括幅度随频率变化的幅频特性和相位随频率变化的相频特性。
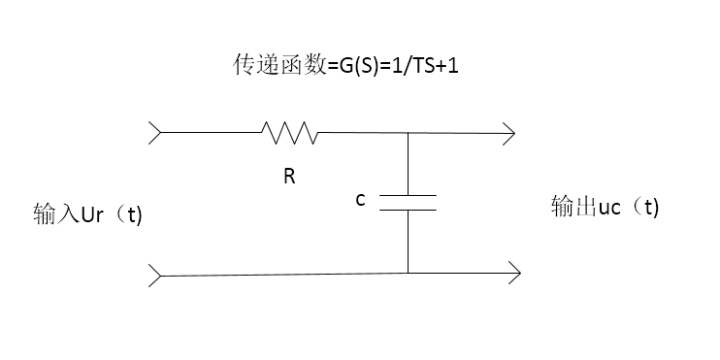
图1
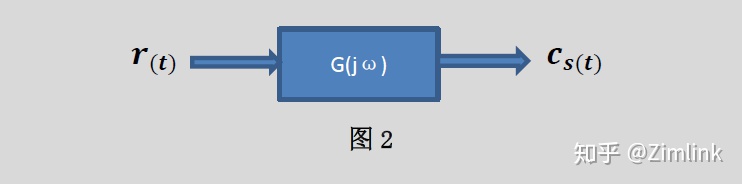
如图1 它的输入信号是正弦信号: Ur(t)=A*sin(ωt),{幅值是A;频率 为(ωt)}
它的电路传递函数:
它的输出:
幅值是:
频率为:
那么幅频特性与相频特性定义如下:
幅频特性=正弦输出与正弦输入幅值比。相频特性=正弦输出相位-正弦输入的相位,或者相角差。
老规矩公式太多了,还是贪下懒吧,下面文章全部改成图片发送(:。






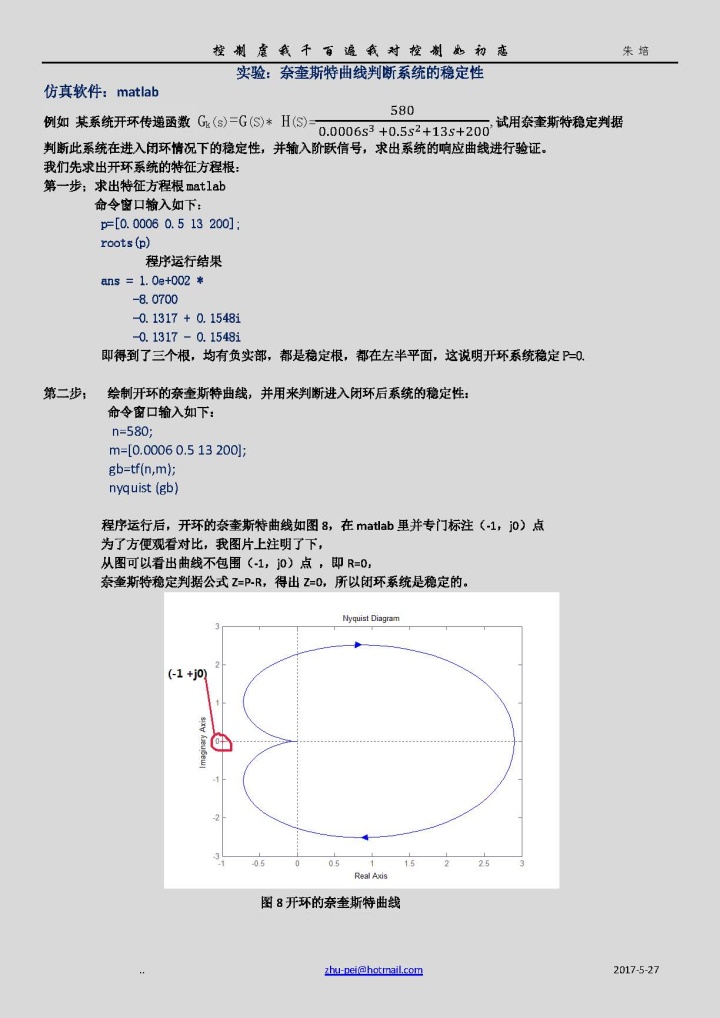
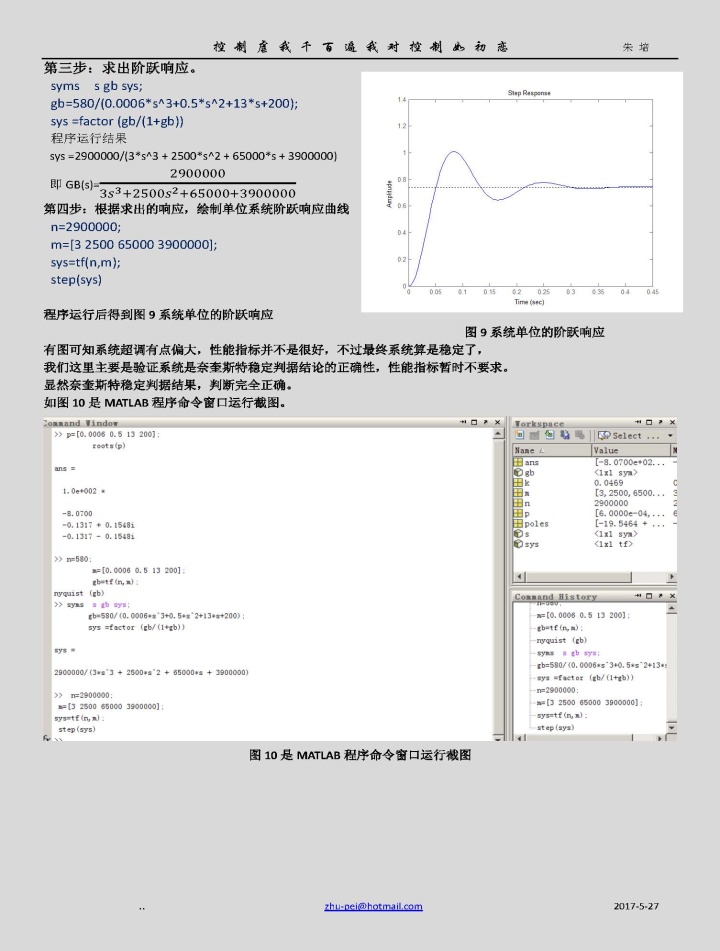
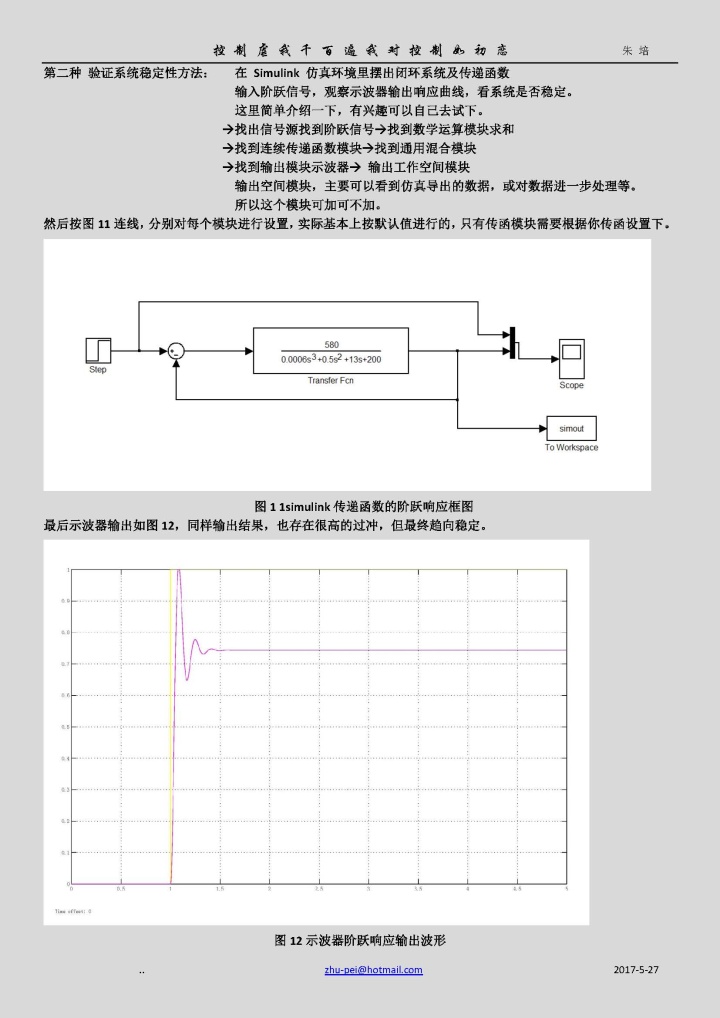
最后
以上就是洁净小鸽子最近收集整理的关于奈奎斯特采样定理_奈奎斯特稳定判据(Nyquist stability criterion)的全部内容,更多相关奈奎斯特采样定理_奈奎斯特稳定判据(Nyquist内容请搜索靠谱客的其他文章。








发表评论 取消回复