一:开环与闭环关系
设负反馈系统的开环传递函数为:
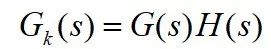 ,
,
其中:G(s)为前向通道传递函数,H(s)为反馈通道传递函数。
闭环传递函数为:
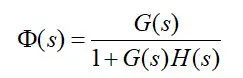
如下图所示:
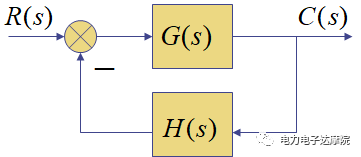
令:
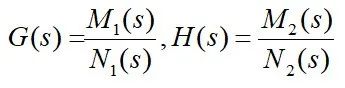
则开环传递函数为:
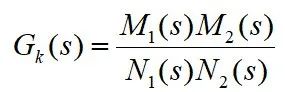
闭环传递函数为:
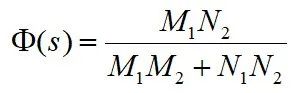
将闭环特征方程与开环特征方程之比构成一个辅助方程,得:
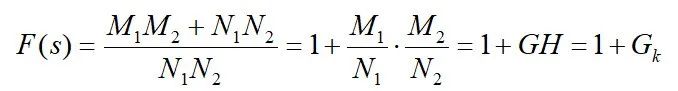
显然,辅助方程即是闭环特征方程。其阶数为n阶,且分子分母同阶。则辅助方程可写成以下形式:
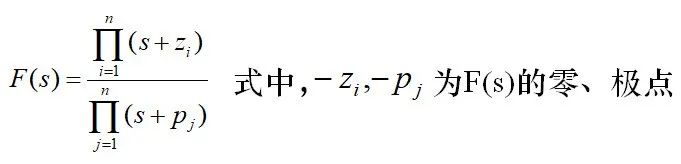
由此可以总结出:
1. F(s)的极点为开环传递函数的极点;
2. F(s)的零点为闭环传递函数的极点;
奈奎斯特稳定性判据是用开环频率特性判别闭环系统的稳定性。不仅能判断系统的绝对稳定性,而且可根据相对稳定的概念,讨论闭环系统的瞬态性能,指出改善系统性能的途径和方法。二:柯西幅角定理
s平面上不通过F(s)任何奇异点的封闭曲线 包围s平面上F(s)的z个零点和p个极点。当s以顺时针方向沿封闭曲线Γs移动一周时,在F(s)平面上相对应于封闭曲线Γf将以顺时针方向绕原点旋转N圈。N,z,p的关系为:N=z-p。1. 若N为正,表示Γf顺时针运动,包围原点;
2. 若N为零,表示Γf顺时针运动,不包围原点;
3. 若N为负,表示Γf逆时针运动,包围原点。
三:奈奎斯特稳定性判据
对于一个控制系统,若其特征根处于s右半平面,则系统是不稳定的。对于上面讨论的辅助方程: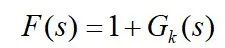
1、如何构造一个能够包围整个s右半平面的封闭曲线,并且它是满足柯西幅角条件的。
2、如何确定相应的映射F(s)对原点的包围次数N,并将它和开环频率特性G(jw)H(jw)相联系。
第一个问题:
假设F(s)在虚轴上没有零、极点。按顺时针方向做一条曲线Γs包围整个s右半平面,这条封闭曲线称为奈魁斯特路径。如下图: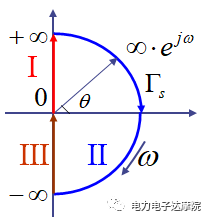
它可分为三部分:
第一部分是正虚轴,w=0→+∞;
第二部分是右半部分半径为无穷大的半圆;
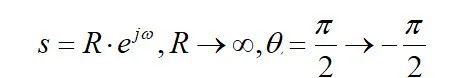
第三部分是负虚轴,w=-∞→0;
F(s)平面上的映射是这样得到的:
以s=jw代入F(s)并令w从0→+∞变化,得第一部分的映射;在F(s)中取
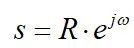
使角度由
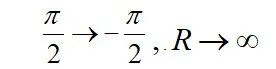
得第二部分的映射;令从w从-∞→0变化,得第三部分的映射。得到映射曲线后,就可由柯西幅角定理计算:
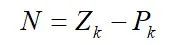
式中:Zk和Pk 是F(s)在s右半平面的零点数和极点数。确定了N,可求出
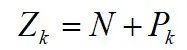
当ZR=0时,系统稳定;否则不稳定。
第二个问题:
辅助方程与开环频率特性的关系。我们所构造的的辅助方程为: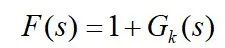
①由Gk(jw)可求得F(jw),而Gk(jw)是开环频率特性。一般在Gk(jw)中,分母阶数比分子阶数高,所以当s→∞时,Gk(s) →0,即F(s)=1。(对应于映射曲线第二部分)
奈魁斯特路径的第一部分的映射是Gk(s)曲线向右移1;第二部分的映射对应Gk(s) =0,即F(s)=1;第三部分的映射是第一部分映射的关于实轴的对称。
②F(s)对原点的包围,相当于Gk(s)对(-1,j0)的包围;因此映射曲线F(s)对原点的包围次数N与Gk(s)对(-1,j0)点的包围的次数一样。
③F(s)的极点就是Gk(s)的极点,因此F(s)在右半平面的极点数就是Gk(s)在右半平面的极点数。
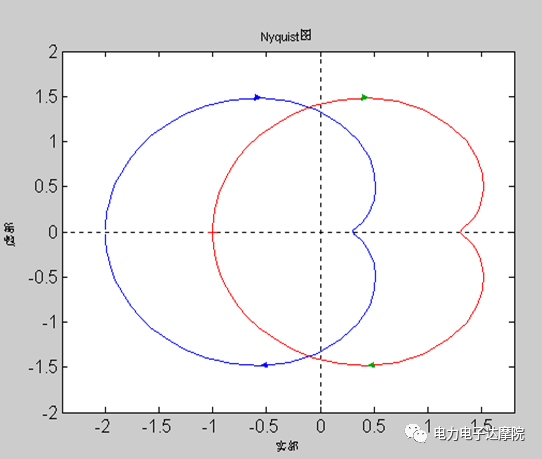
奈奎斯特稳定性判据:
系统的开环传递函数在右半平面上有Pk个极点,且开环频率特性曲线对(-1,j0)点包围的次数为N,(N>0顺时针,N<0逆时针),则闭环系统在右半平面的极点数为: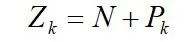
最后
以上就是冷酷便当最近收集整理的关于稳定判据_自动控制系统时域分析十五:奈奎斯特稳定性判据的全部内容,更多相关稳定判据_自动控制系统时域分析十五内容请搜索靠谱客的其他文章。








发表评论 取消回复