一、取样定理
其实奈奎斯特采样有两种方式,一种是矩形脉冲采样,一种是冲激采样,采样方式如下图。我们在不计算数学公式的情况下来讲解,只是让大家明白是这么回事,具体为什么是这样,是有一堆公式要推导的。
1.知识准备
2.矩形脉冲采样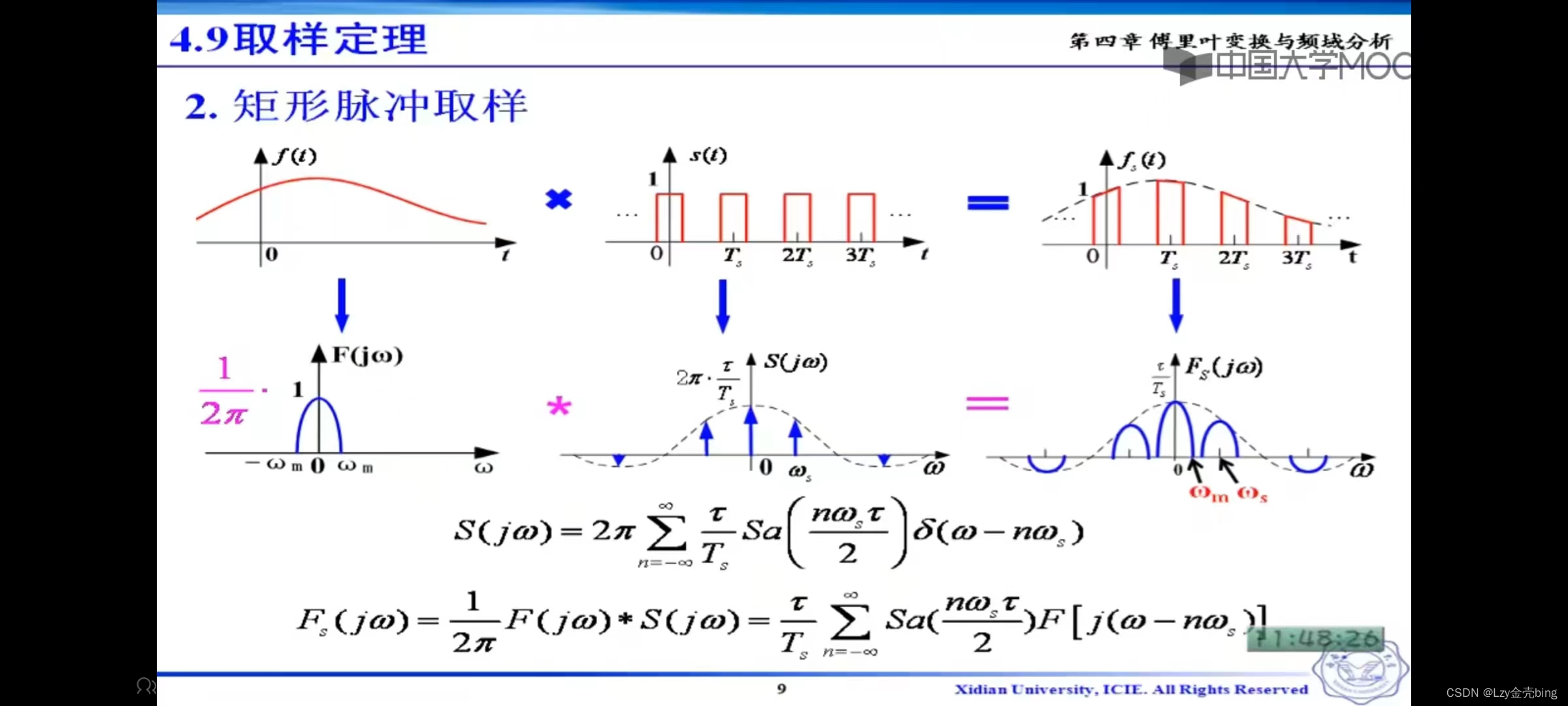
矩形脉冲采样图解:图上第一排表示在时域上,一个有限带宽的信号(原始信号)X 周期(周期为T)矩形脉冲信号 = 原始信号的离散型。第二排表示将第一排的信号从时域上傅里叶变换到频域上,再进行卷积(时域上的乘积等于频域上卷积)。最后卷积出的信号在频域上就出现了无数个周期性(周期为1/Ts)的、带宽(2ωm)相同、但是幅度不同的原始信号。
3.冲激采样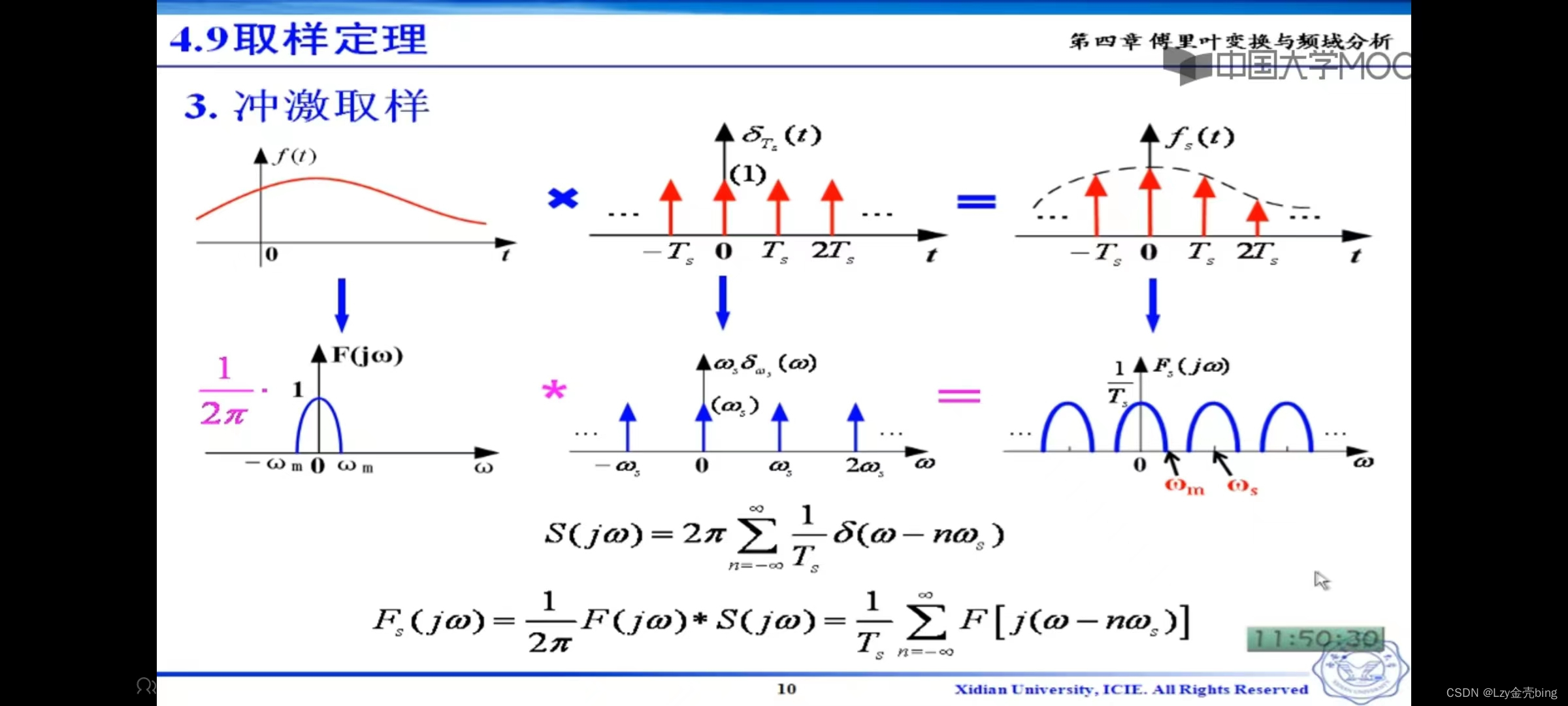
冲激采样图解:图上第一排表示在时域上,一个有限带宽的信号(原始信号)X 周期(周期为T)冲激信号 = 原始信号的离散型。第二排表示将第一排的信号从时域上傅里叶变换到频域上,再进行卷积(时域上的乘积等于频域上卷积)。最后卷积出的信号在频域上就出现了无数个周期性(周期为1/Ts)的、带宽(2ωm)相同、幅度相同的原始信号。
3.结论
频谱延拓:对于一个连续的信号采样,采样后的频谱相当于将采样前的频谱进行延拓,延拓的周期就是采样率。
奈奎斯特采样定律:如冲激取样卷积后的图像图示,要避免频谱出现混叠,频谱不能有重合,必须有ωs ≥ 2ωm(ωm为原始信号的最高频率)。这就得到了经典的奈奎斯特采样定律:要从抽样信号中无失真地恢复原信号,抽样频率应大于2倍信号最高频率。
在实际应用情况中,并不能实现有效的冲激取样,所以AD、DA设备的采样都是脉冲采样。
二、镜像频谱
上面我们说到频谱延拓,就我理解而言,无论是镜像频谱还是频谱的对称性,都是频谱延拓延伸出来的性质。我们通过下图来分析一下镜像频谱产生的原因。
下图3为DDS在300M主频,输出80M频率时的频谱。
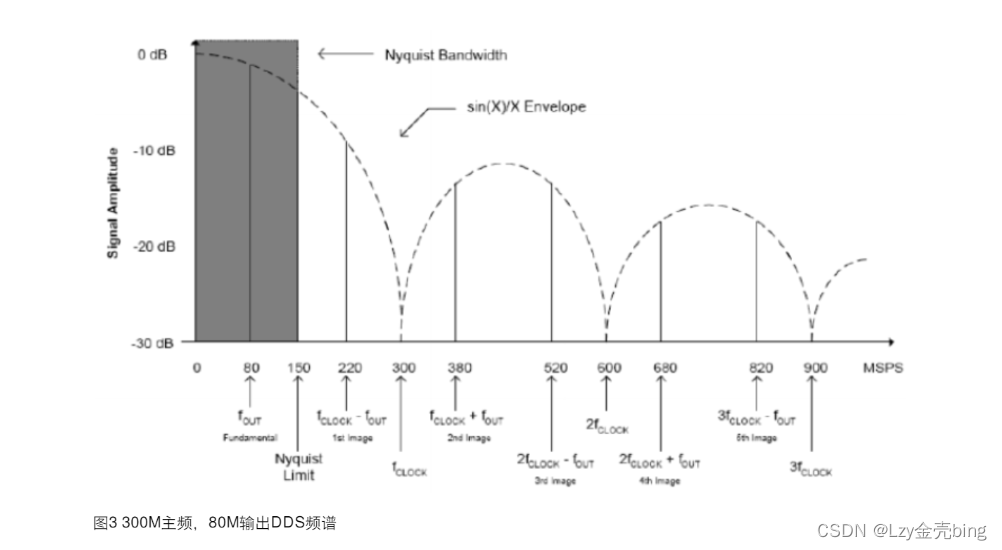
我们上面说过,实际应用中的采样都是脉冲采样,所以可以看出80M信号300M采样率为周期延拓出来,幅度逐渐降低。但是220M、520M、820M又是怎样出现的呢,这里我先给出结论,这些就是原始80M信号的镜像频谱。下面我们来推导一下:s = sin(2*pi*ω*t)
原始信号s0 = sin(2*pi*80*t)(频域上的采样率就表示ω),以300M为周期进行采样T=1/f,
x0[k] = sin( 2*pi*80*(1/300*k) )(k=0、1、2……)(k的意义就是在0T上采一个点、在1T上采一个点、在2T上采一个点……)
我们把x0[k]换一种写法x0[k] = sin( 2*pi*(300-220)*(1/300*k) )
= sin( 2*pi*300*(1/300*k) - 2*pi*220*(1/300*k))
= sin( 2*pi*k - 2*pi*220*(1/300*k))
= - sin( 2*pi*220*(1/300*k))
也就是说x0[k] = sin( 2*pi*80*(1/300*k) ) = - sin( 2*pi*220*(1/300*k)),看出来了吗?
再总结一下:假设一个频率是f0(令其小于fs/2),另外一个频率是fs - f0,其中fs是采样频率,则
x[k] = sin(2*pi*(fs-f0) * 1/fs * k )
= sin(2*pi*k - 2*pi*f0*1/fs*k)
= -sin(2*pi*f0*1/fs*k)
所以,fs - f0频率的sine波,与f0频率的sine波,在用fs采样率来采样的话,会得到频率相同,幅度大小相同,相位相反的序列,这就是镜像频频谱。
我们换个角度来讲: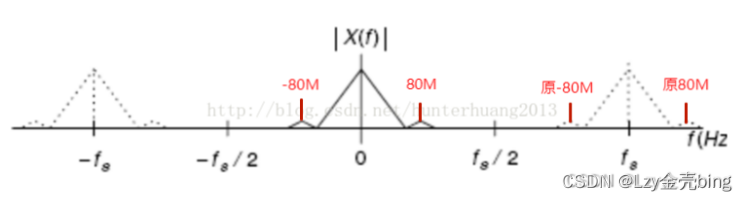
理论上由于信号双边谱特性,有80M信号就有镜像的-80M信号,fs=300M,根据频谱拓延,向右平移一个周期,就得到如图标注的样子,在fs内,有一个80M的频谱和原-80M的频谱,-80M的频谱横坐标就是220M。个人理解也是能解释为什么会有镜像频谱。
三、带通采样
为什么要用带通采样定理呢?按理说,奈奎斯特采样定理不是通吃一切吗?话虽如此,奈奎斯特说,只要采样率不小于信号最高频率的2倍,采样后的信号就能能够准确恢复。
可事实上,有很多行不通的地方,并不是说理论行不通,而是器件做不到,对于频带信号(带通信号)而言,例如天线发出的信号以及接收的信号,可以说都是频带信号,因为频带信号便于传输,这些信号的频率随着时代的进步,也越来越大,电磁信号向着GHz甚至数十GHz发展,如果再用奈奎斯特采样定理采样,如此之高的采样率ADC恐怕难以做到吧。
1.带通采样原理
我们来看下图(双边谱图):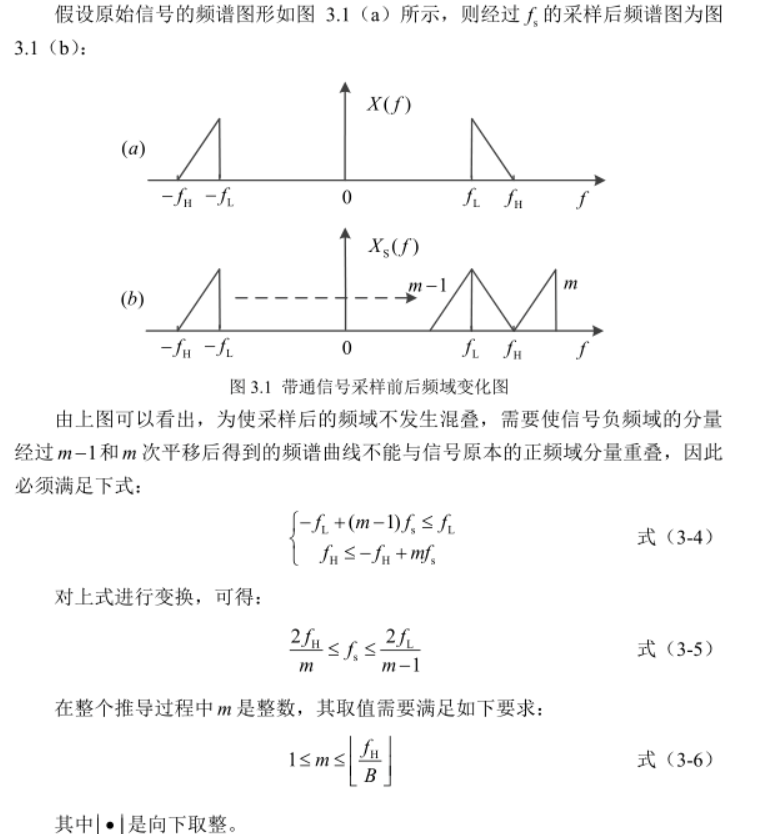
图解:(a)是原始信号频谱,(b)是经过频谱拓延后的频谱。我们上面结论里提到的频谱拓延一个重要的参数就是延拓的周期,也就是采样率fs,记住这点。
(b)中,在我们不知道fs具体是多少的情况下,也就是fs可以是任意值时,频谱可以随意拓延,但是随意拓延会造成频谱混叠,我们要恢复原始信号就不能有频谱混叠的现象出现,所以有式(3-4)的规定:负频域的频谱频移m次后,不能与原始信号混叠(不与原始信号混叠也就不会与原始信号的频移频谱混叠,你可以画图举个具体的例子自己看一下),那就有-fH + mfs ≥ fH。你的上一次(m-1)频谱频移也不能与原始信号混叠,那就有 -fL + (m-1)fs ≤ fL。整理后得到式(3-5)。
式(3-6)中 fH/B 计算最多可以向0频处进行多少次频移,因为采用带宽采样为的是降低采样率,越靠近0频,采样率越低(单看正半轴上的频谱就可以,最终要保证采样率落在正半轴上)。
2.如何确定带通采样后的频谱中心位置,以进行下变频
设采样率fs,信号中心f0,信号带宽上下限fh,fl。有2种情况,
A fs<f0
假设f0= 2.75G, fh=2.5,fl=3,根据上图公1<=m<=6,例如去m=3,得2<=fs<=2.5,取fs = 2G,其带通采样后的频谱如图2所示,可以看到通过对称、周期延拓性质,离零频最近的信号中心为0.75G=f0-fs。因此设置ADC的下变频NCO = 0.75G。
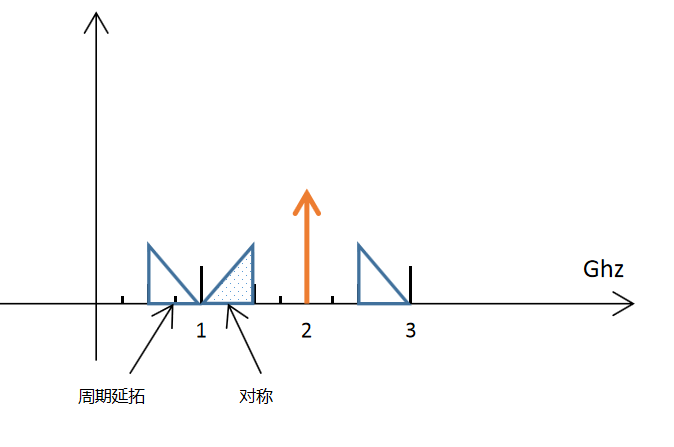
图2 fs<f0
B fs>f0
假设f0= 2.75G, fh=2.5,fl=3,根据上图公1<=m<=6,例如去m=2,得3<=fs<=5,取fs = 3G,其带通采样后的频谱如图3,
可以看到通过对称、周期延拓性质,离零频最近的信号中心为0.25G=fs-f0(不过是镜像频率)。因此设置ADC的下变频NCO = 0.25G。
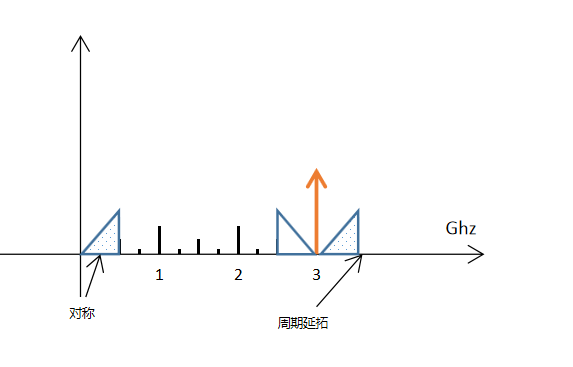
图3 fs>f0
总结:带通采样后的信号中心频率F = |fs-f0|。我们应尽在ADC采样范围内尽可能将采样率取高些,且采样率最好是有用信号带宽的整数倍,这样便于抽取滤波。
最后
以上就是调皮橘子最近收集整理的关于小白能理解的奈奎斯特采样及延伸出的理论1.带通采样原理 2.如何确定带通采样后的频谱中心位置,以进行下变频的全部内容,更多相关小白能理解内容请搜索靠谱客的其他文章。








发表评论 取消回复