要点
1、零极点图绘制
2、根轨迹图绘制
3、 rlocfind()函数
4、 sgrid()函数
实操

3-1
k=1;
num=[1 2 2];
den=conv([1,0],conv([1,4],conv([1,6],[1,4,4])));
[p,z]=pzmap(num,den)
G=zpk(z,p,k)
figure(1);pzmap(G)
figure(2);rlocus(G)
title('系统 G(s)=k(s+1)/s*(s-1)*(s^2+4*s+16)根轨迹图');
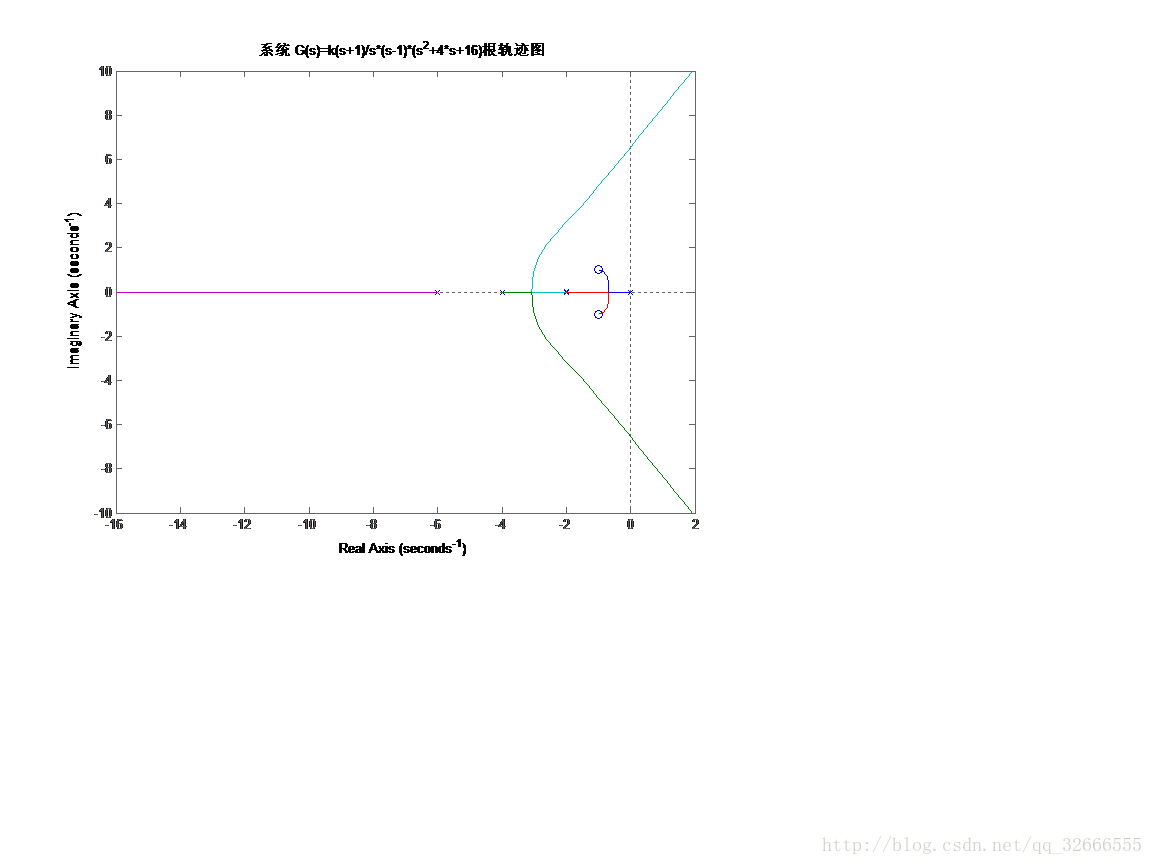
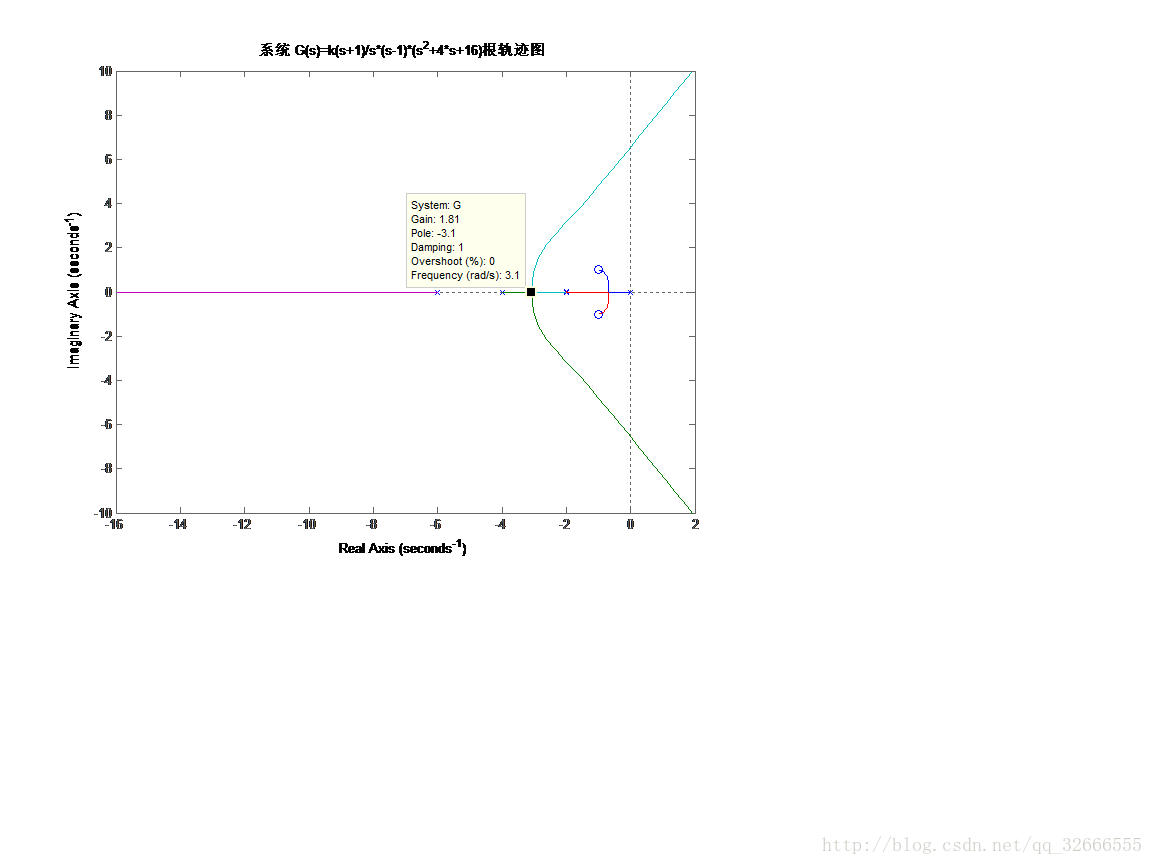
由图得分离点 d=-3.1,相应的根轨迹增益 k=1.81 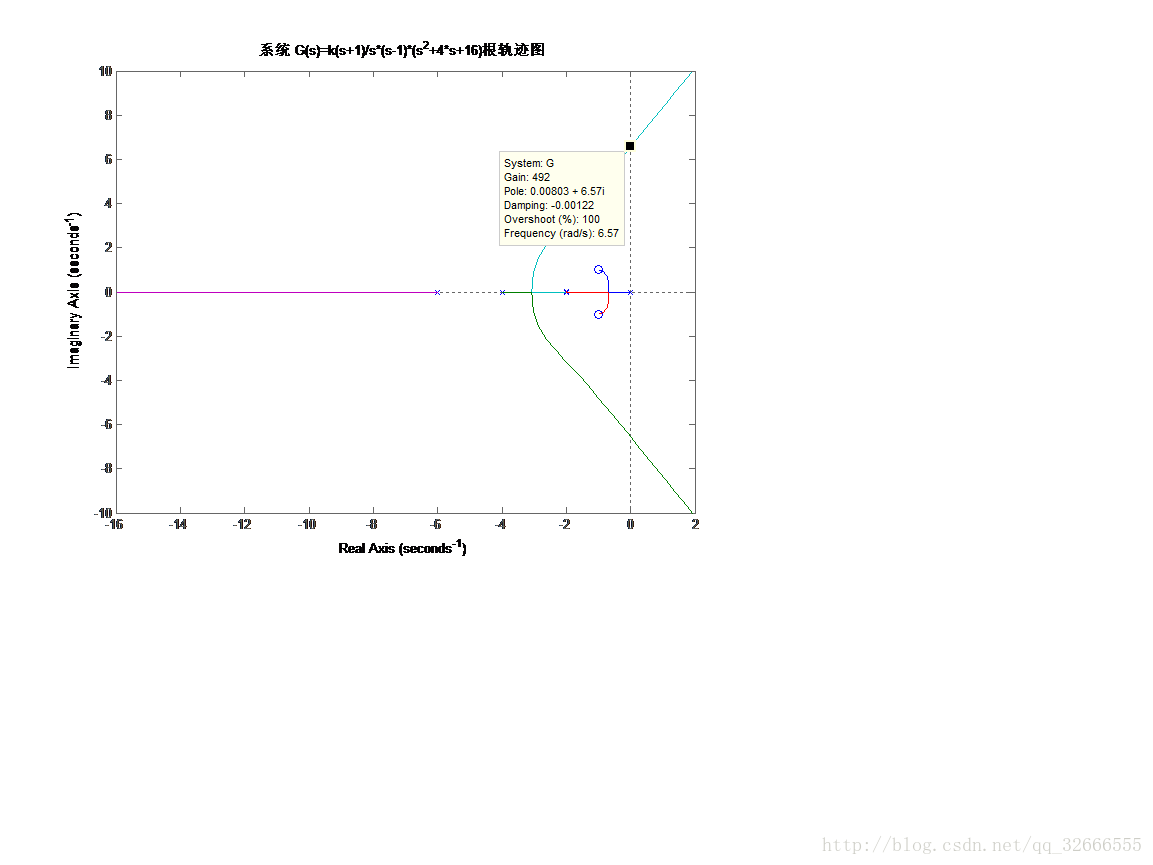
由图得临界根轨迹增益kcr =492
3-2
num=[1 1];
den=conv([1,0],conv([1,-1],[1,4,16]));
rlocus(num,den)
[k,p]=rlocfind(num,den)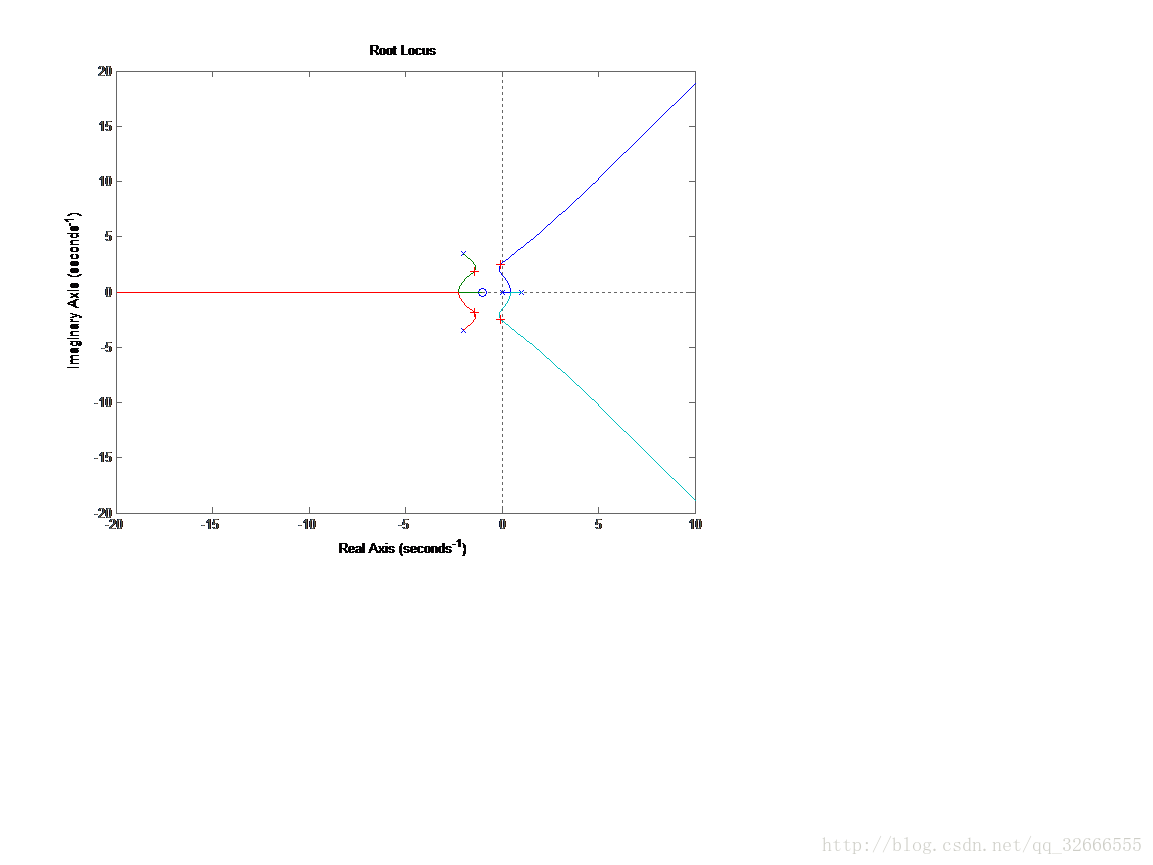
调用rlocfind()函数,求出系统与虚轴交点的K值,可得与虚轴交点的K值为34.0224,故系统稳定的K的范围为(0, 34.0224)
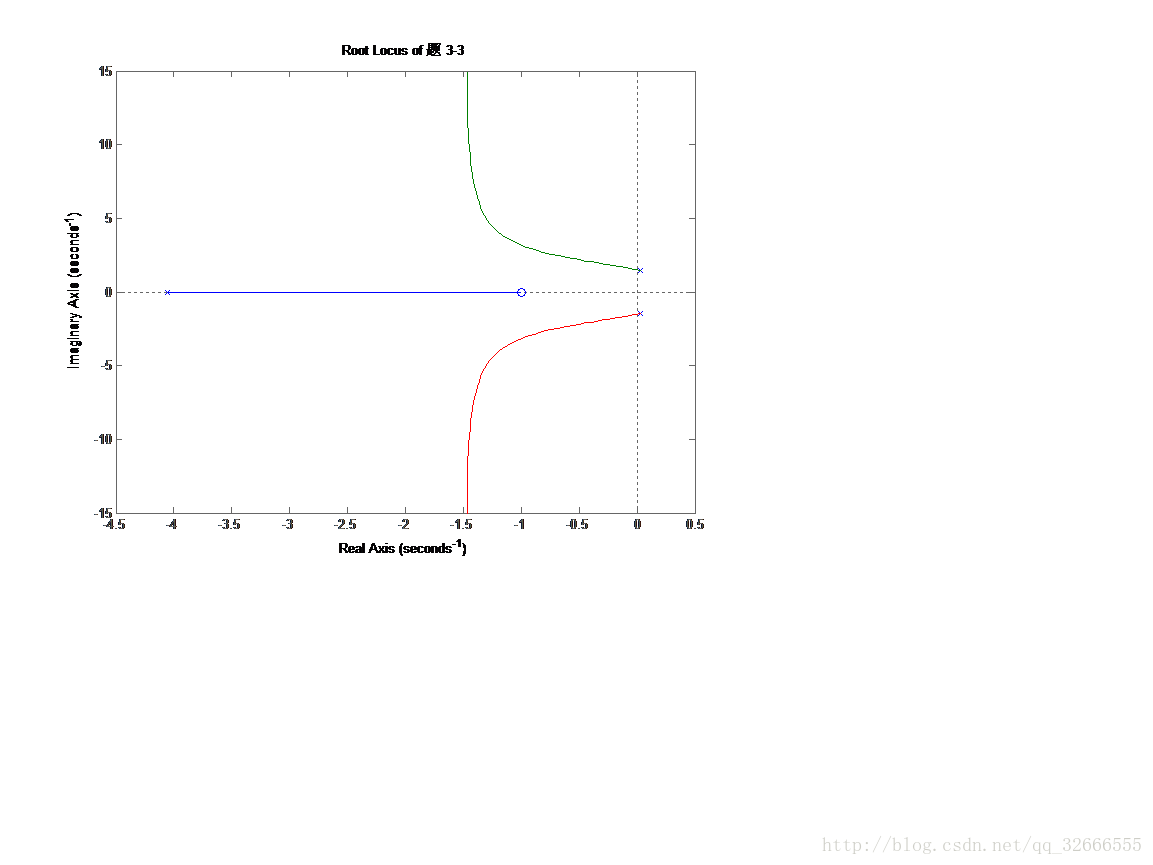
3-3
num=[1 1];
den=[1 4 2 9];
figure(1);rlocus(num,den)
title('Root Locus of 题 3-3');
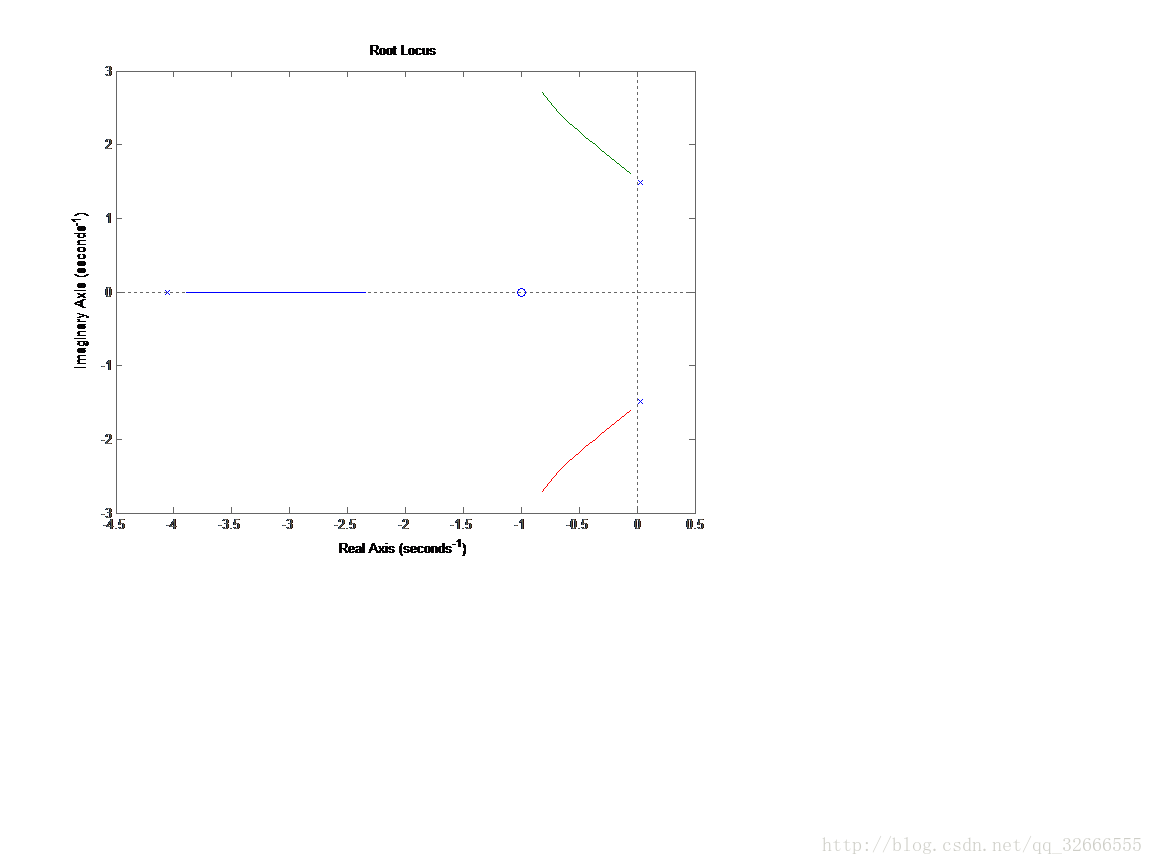
k=1:0.5:10;
figure(2);rlocus (num,den,k)
3-4
z=[];
p=[0 0 -2 -5];
k=[1];
[num,den]=zp2tf(z,p,k);
figure(1);rlocus(num,den)
z1=[-0.5];
[num1,den1]=zp2tf(z1,p,k);
figure(2);rlocus(num1,den1)
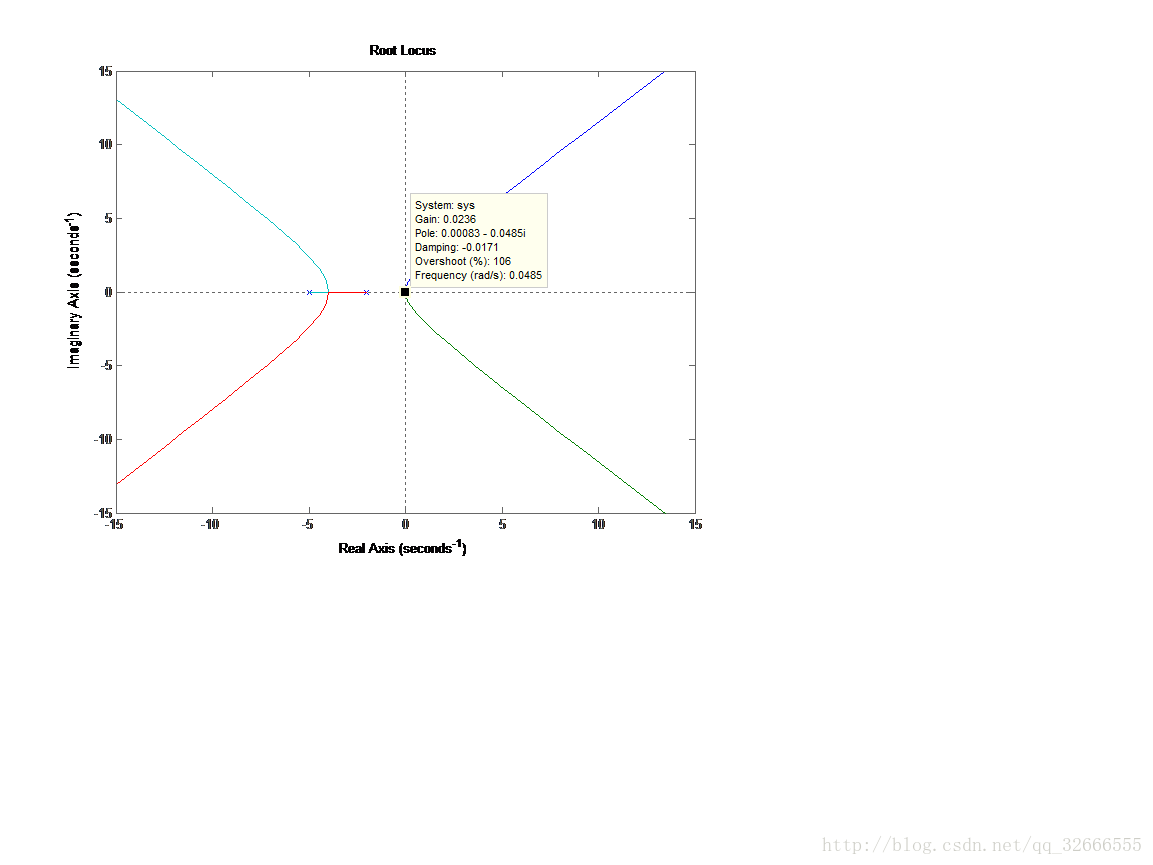
无论K取何值,系统都不稳定。
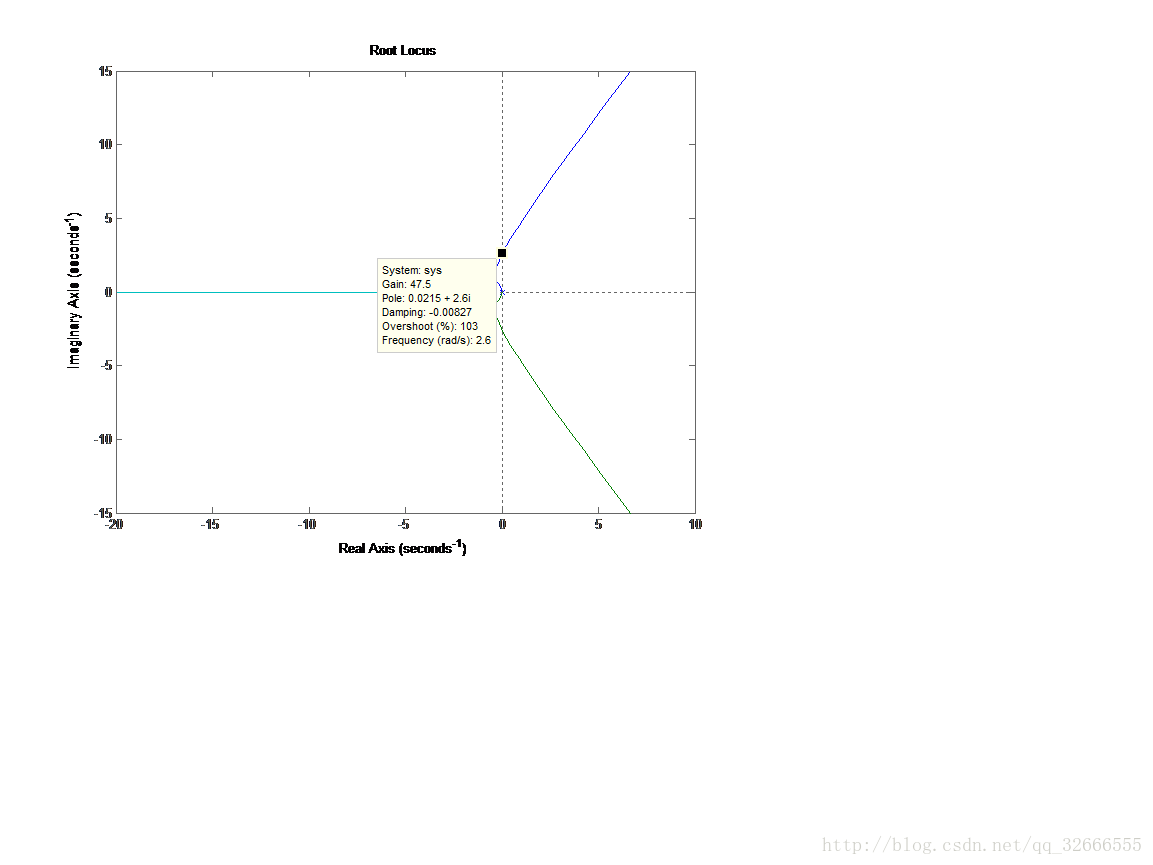
加入零点-0.5后,当K<47.5时,系统稳定。
分析:增加负零点后,系统根轨迹向S左半平面凹陷弯曲,,因此能够一定地增强系统稳定性。
最后
以上就是魔幻指甲油最近收集整理的关于MATLAB实现控制系统的根轨迹分析的全部内容,更多相关MATLAB实现控制系统内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复