滑模控制原理_如何给电机控制系统加上ESO进行扰动补偿

0. 概述

ESO又名扩张状态观测器，其本质是将控制系统中存在的所有不确定扰动看作一个整体（集总扰动d，并且要求是匹配扰动），将其定义成一个新的状态变量xn+1，称之为扩张状态。这样利用状态观测器的原理就能够将集总扰动估计出来，再通过一定的方法将这个扰动给消掉，就能够提升系统的性能了。

1. 系统分析

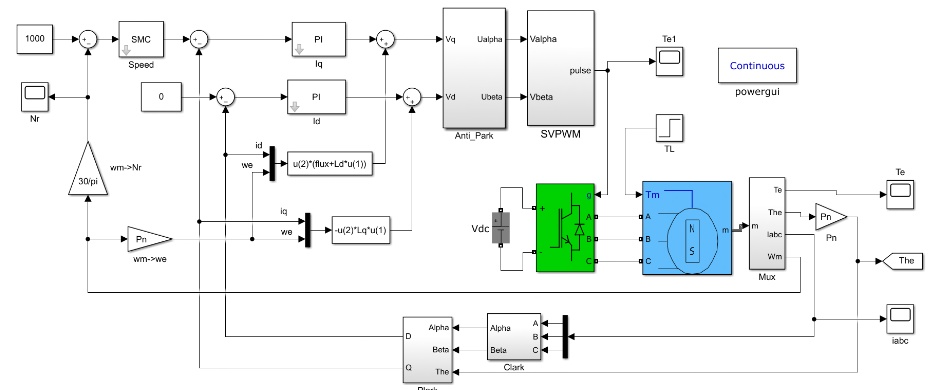
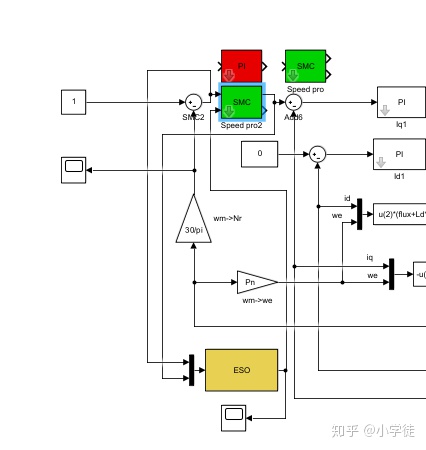
电机系统是已经设计好的，主要是利用一个滑模控制器作为速率环控制器进行电机转速的伺服控制，后面的是一些坐标变换、SVPWM等仿真模块，可暂时不去关注他们，如图。

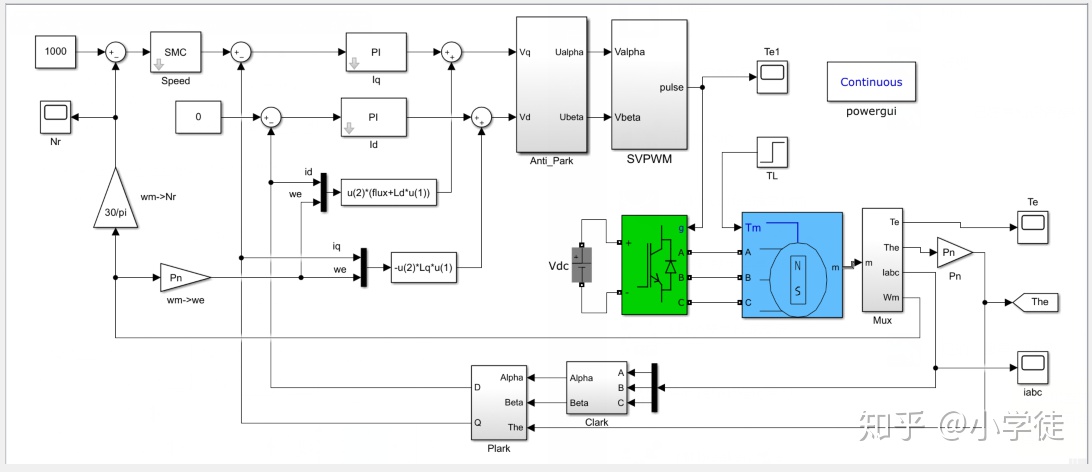
假设一个电机，他的负载是恒定的，这个时候如果收到了外部的扰动产生了扰动力矩，这里设置为了TL，那么电机能否依然保持在指定转速是电机性能的一个关键指标。当我们不知道这个外部扰动力矩的时候，我们只能通过滑模控制器对误差的收敛性来进行抑制，当我的外部扰动较大的时候，速率曲线就会是这个样子。

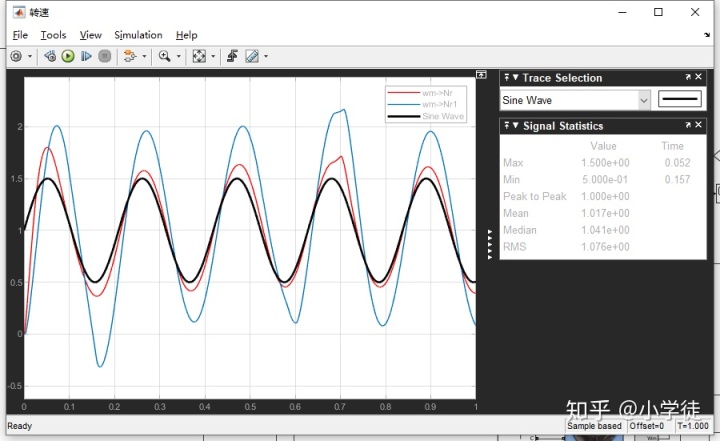
可见，存在较大的误差。伺服性能还有上升的空间。这个时候需要对系统模型进行分析，看一看扰动是怎样作用在系统当中的：

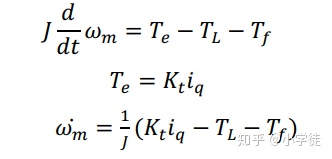
可见，基本原理是角加速度乘以转动惯量为负载力矩，电机转矩Te包含了负载力矩（J×a）、扰动力矩（TL其实应该写作Td 是扰动的意思）和摩擦力矩。其中扰动和摩擦是造成误差的关键，而且是不确定的。如果能够消去他们，那么系统将获得更好的控制性能。

2.设计方法

这篇文章所讲的ESO能够把集总扰动给估计出来然后在原系统中把他们给补偿掉。ESO的方法相关论文很多，这里只是简单的应用。

定义系统状态：

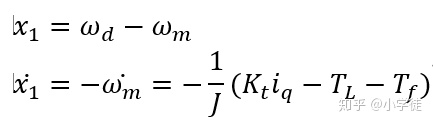
角速率跟踪误差为状态x1，将扰动项作为集总扰动，即设1/J（TL+Tf）为扩张状态x2，则构建状态空间方程：

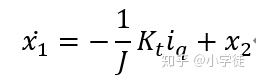
这个形式是满足积分串联形式的，符合ESO的设计条件。参考高志强老师的论文中所讲的ESO设计方法，本文的系统则更加简单。

根据LESO参数整定方法（见之前文章）可以对观测器参数p进行设置，matlab代码如下(这里已经把具体的系统参数代入了，不是很规范，所以会有各种小数存在，关注方法即可)：

通过ESO把x2估计出来然后，参考上图中的式4.7，在控制器中进行补偿即可。

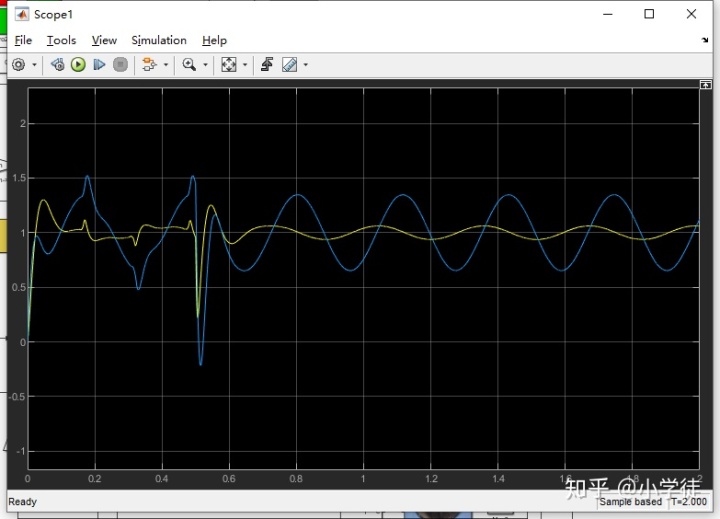
下图为Simulink仿真出来的：系统在正弦扰动下的角速率跟踪曲线。可以看到，加上ESO扰动补偿的系统对扰动的抑制效果明显优于原始系统。

参考文献：

[1] Gao Z . Scaling and bandwidth-parameterization based controller tuning[J]. 2003.

[2] 袁雷等.现代永磁同步电机控制原理及 MATLAB 仿真[M]．北京:北京航空航天大学出版社， 2016.3