系统 动态方程、控制输入及事件触发条件分别如式(2.1)、(3.1)及式(3.6)所示。

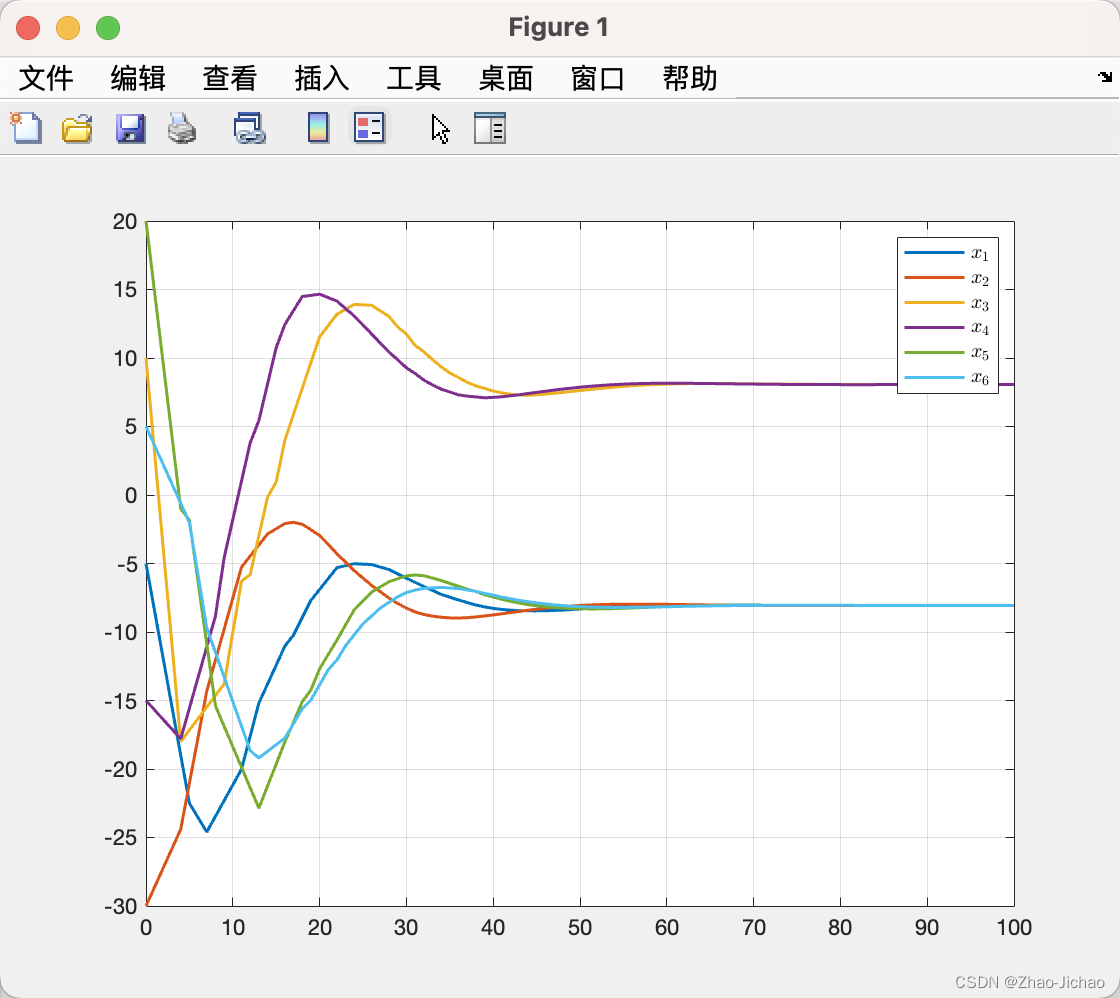
本文考虑一阶离散多智能体系统，第 $i$ 个智能体的动态方程如下:

$$\begin{array}{rl}{x}_i(k+1)& =x_i(k)+u_i(k)\end{array}\text{\hspace{1em}(2.1)}$$

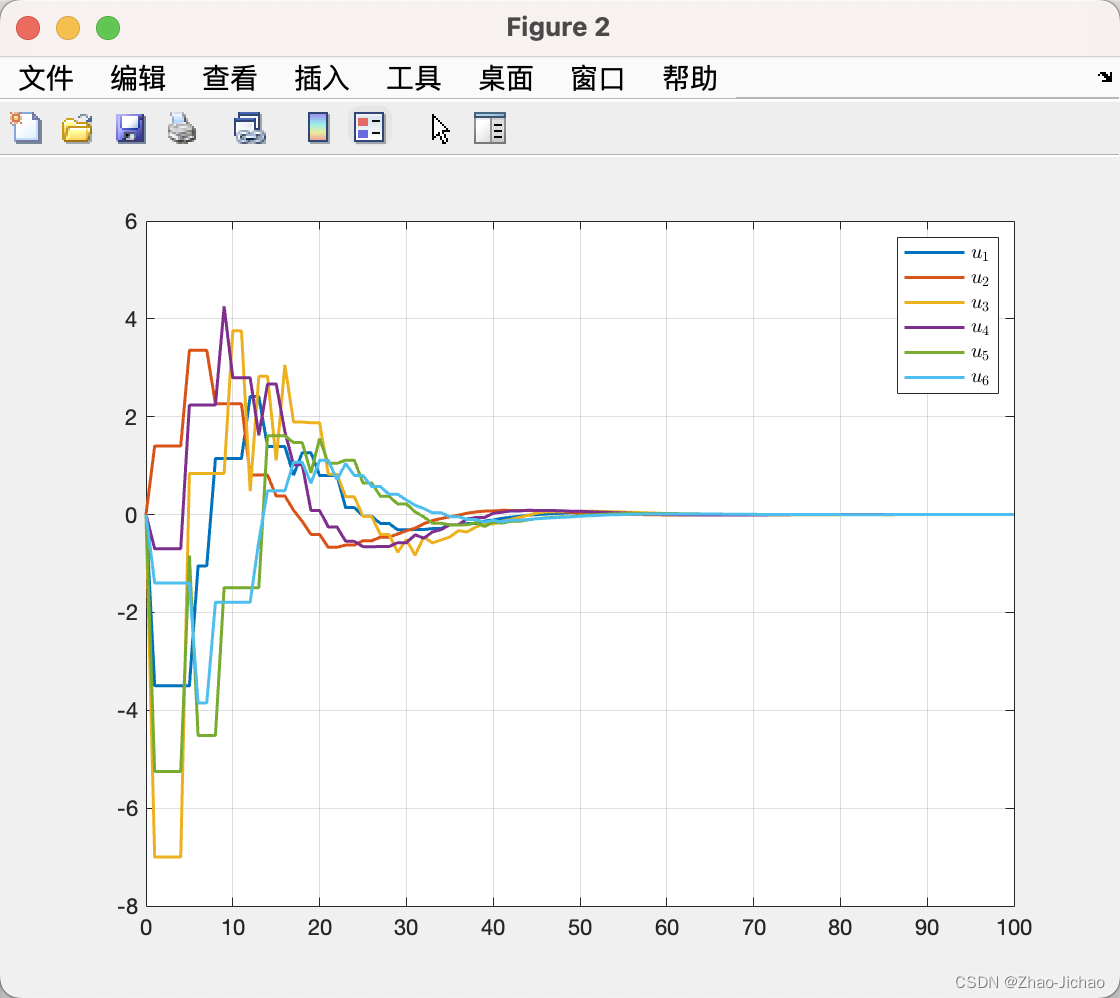
基于文献 [48] 中给出的连续型二分一致性控制输入，我们给出事件触发二分一 致性控制输入，如下：

$$\begin{array}{rl}{u}_i(k)& =-ϵ\sum _{j\in N_i^{in}}|a_{ij}|[{\hat{x}}_i(k)-\text{sign}(a_{ij}){\hat{x}}_j(k)]\end{array}\text{\hspace{1em}(3.1)}$$

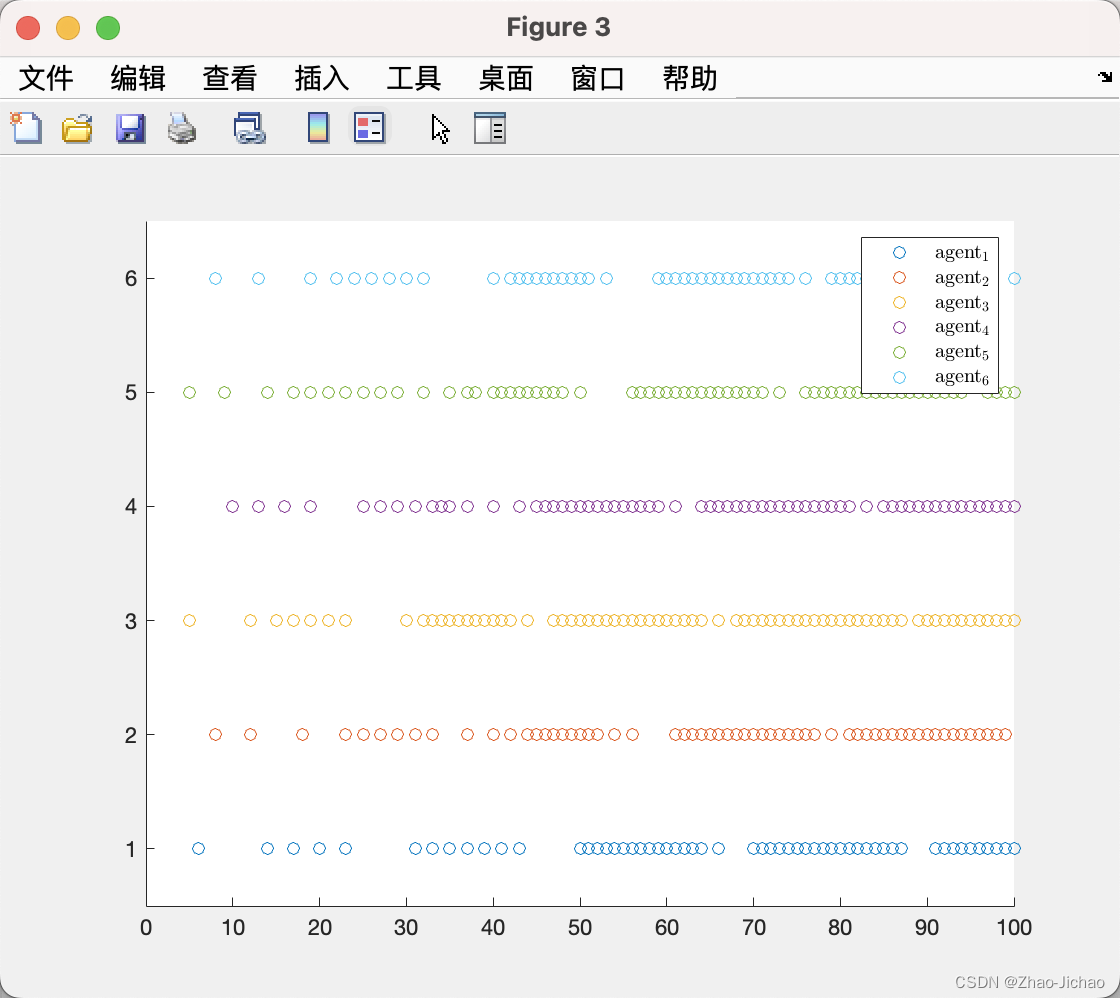
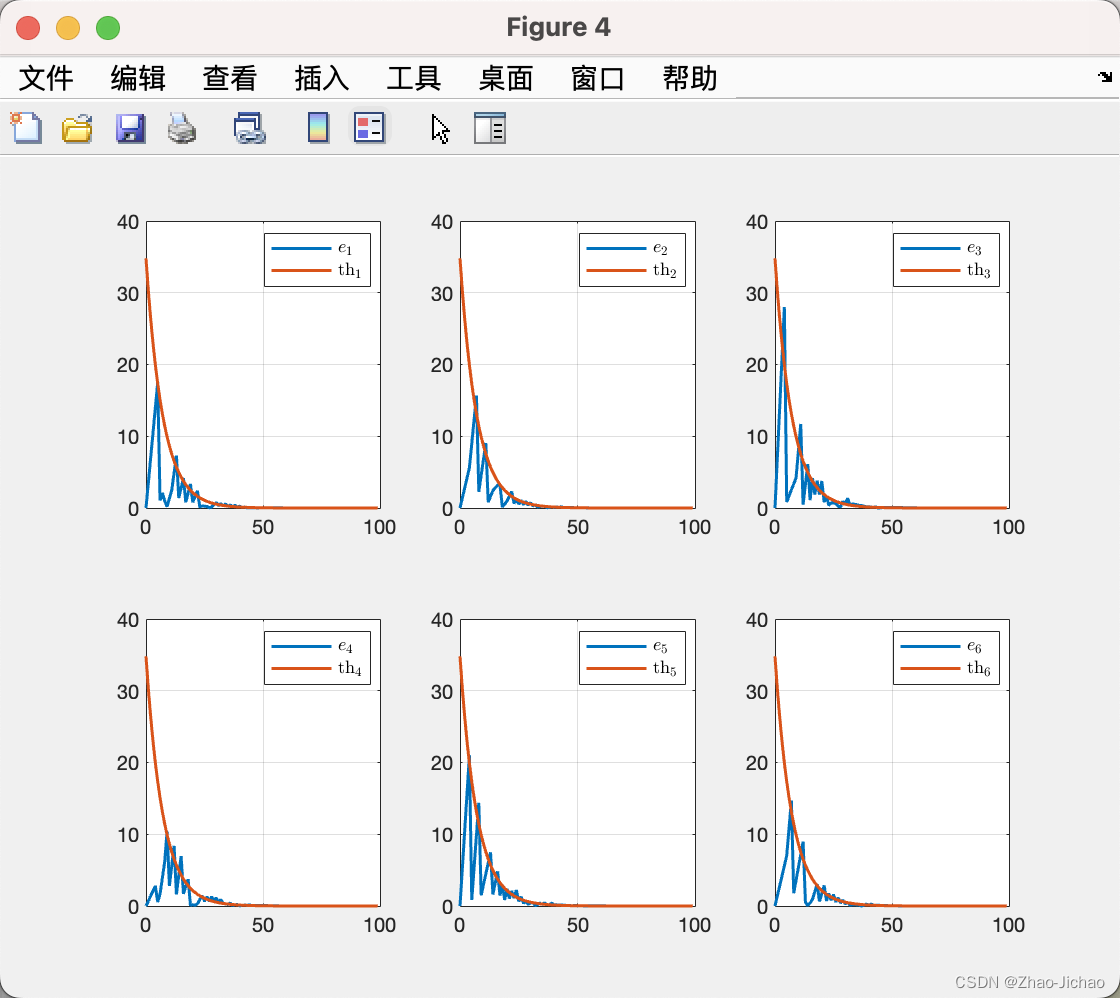
定义事件触发条件为：

k σ + 1 i = inf ⁡ { k : k > k σ i , ∣ e i ( k ) ∣ ≥ β α k } (3.6) begin{aligned} k_{sigma + 1}^{i} &= inf { k: k > k_sigma^i, |e_i(k)| ge beta alpha^k } end{aligned}tag{3.6} kσ+1i​​=inf{k:k>kσi​,∣ei​(k)∣≥βαk}​(3.6)

第 4 章 有向符号图下离散多智能体系统的事件触发二分一致性

4.3.1 示例一

对应程序 Main_Ex4_3_1.m

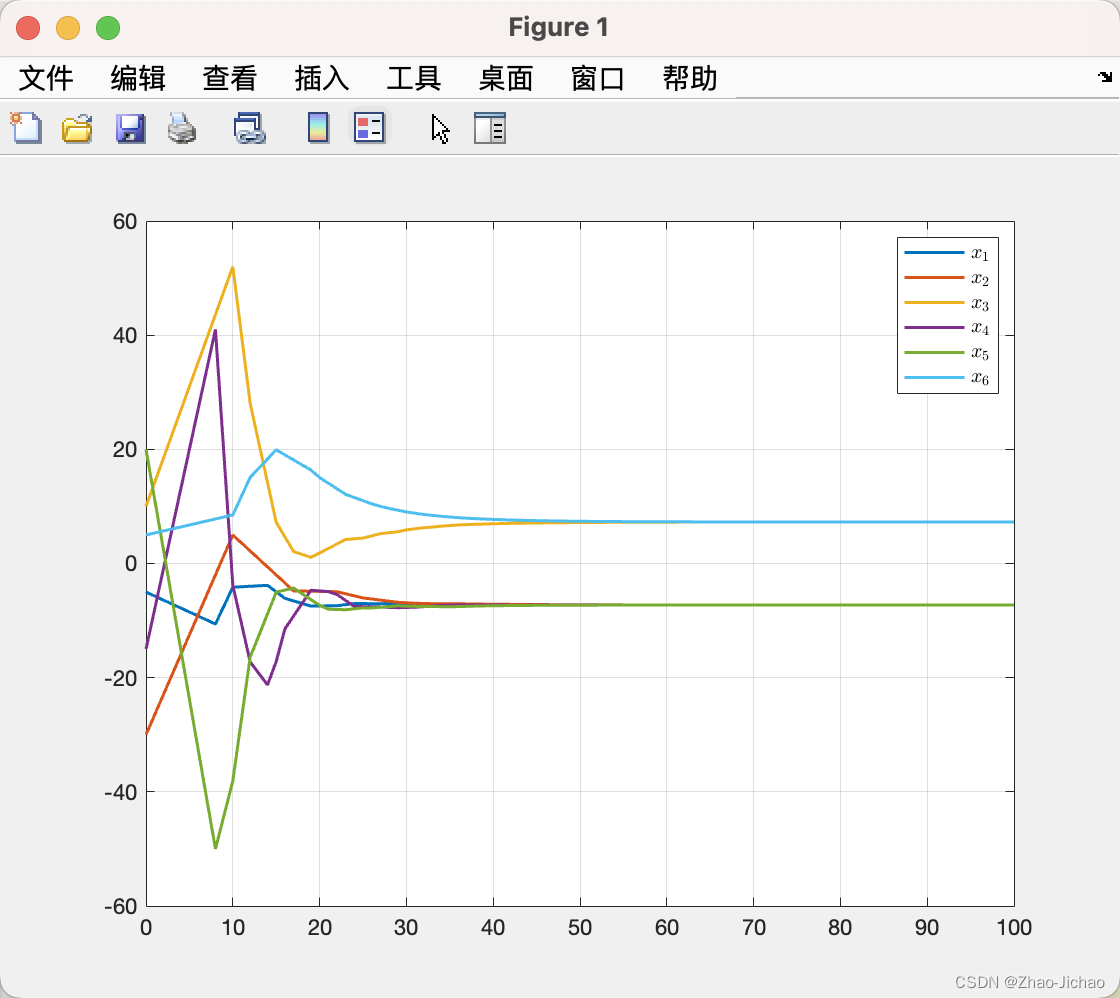
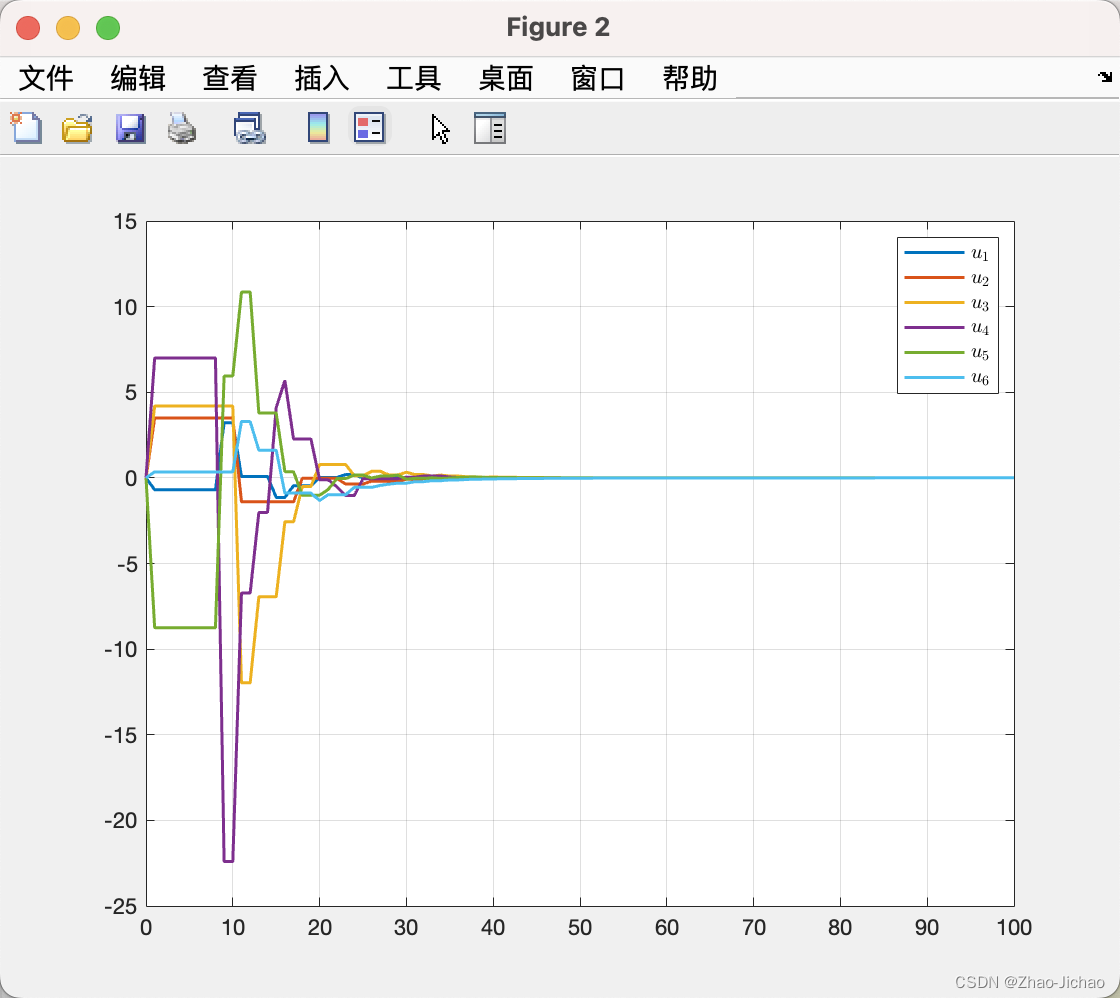
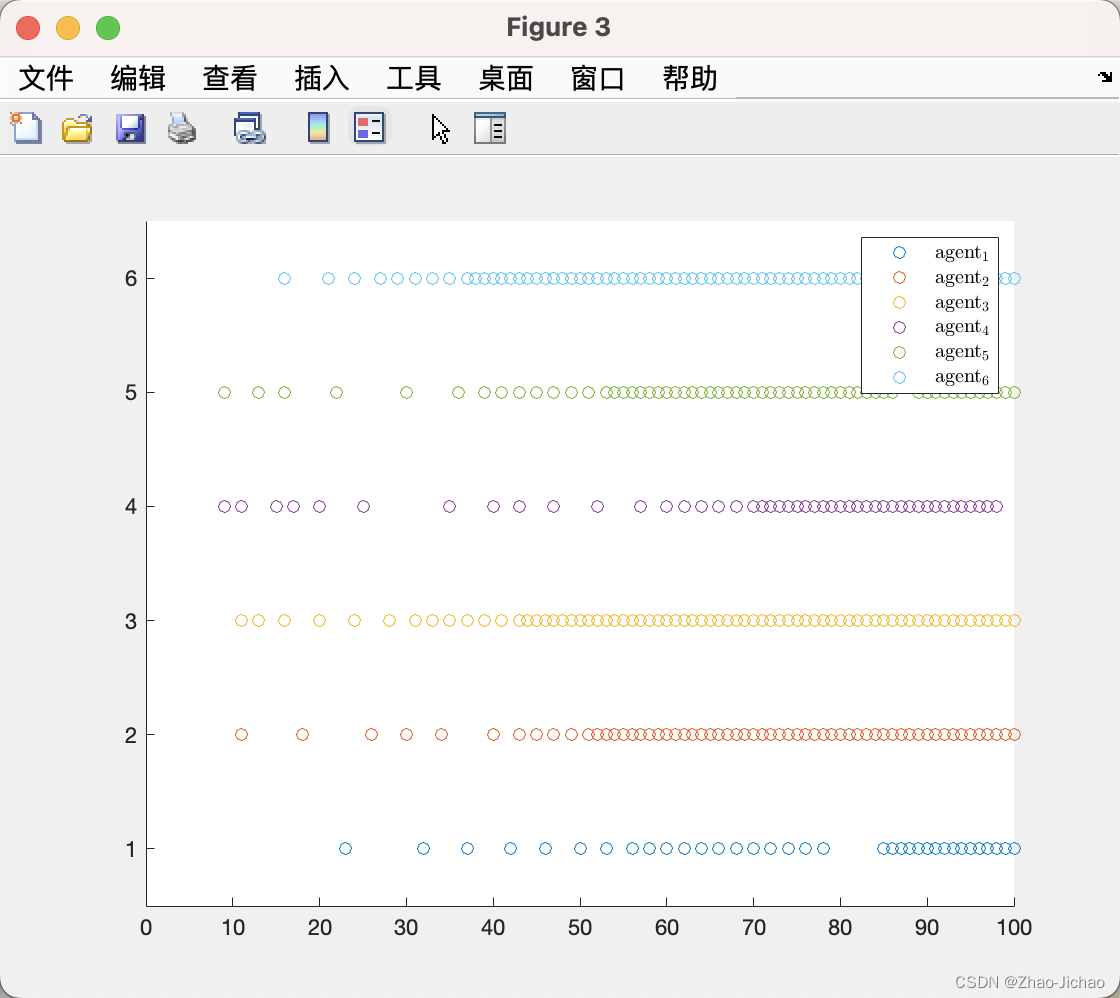
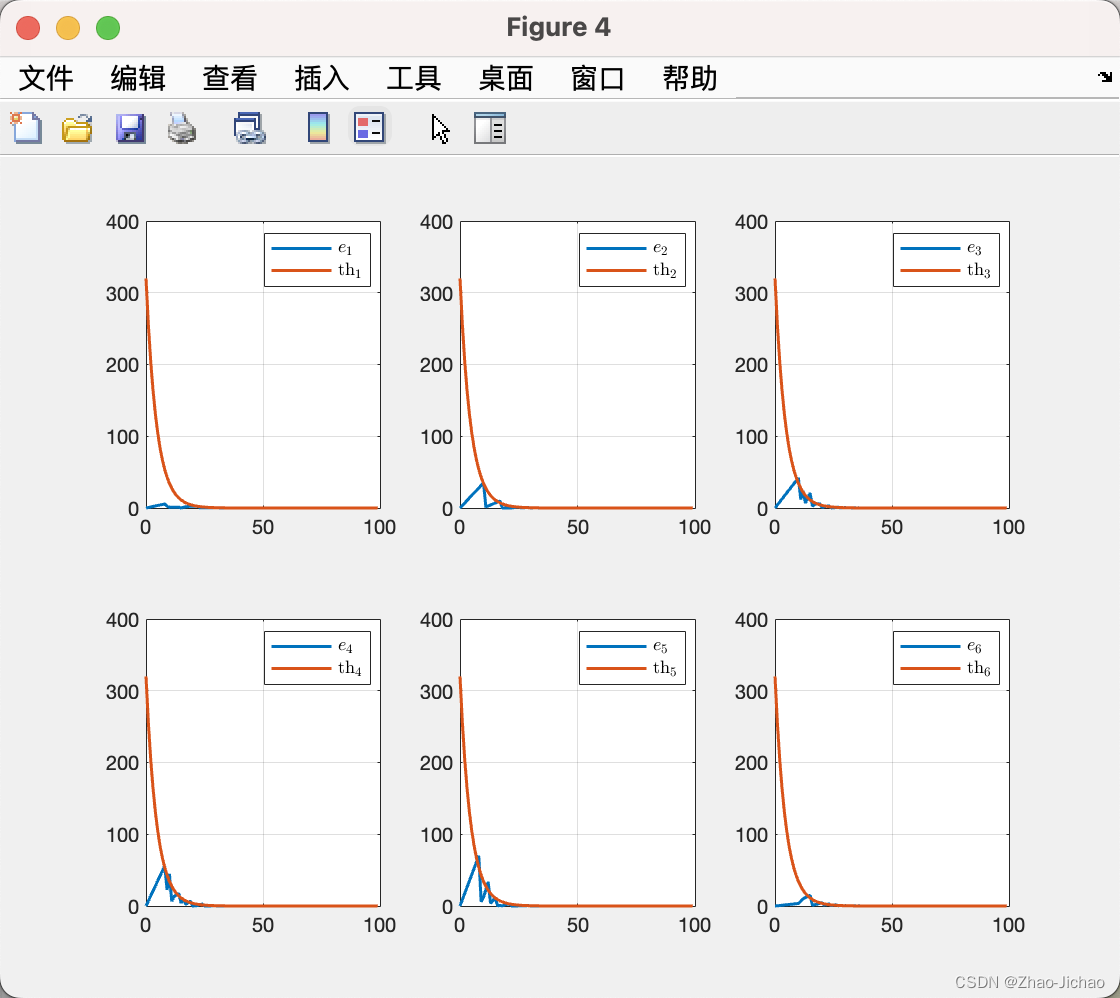
4.3.2 示例二

对应程序 Main_Ex4_3_2.m

最后

以上就是自觉水杯为你收集整理的【Paper】2020_离散多智能体系统的事件触发二分一致性研究_刘雨欣第 4 章 有向符号图下离散多智能体系统的事件触发二分一致性的全部内容，希望文章能够帮你解决【Paper】2020_离散多智能体系统的事件触发二分一致性研究_刘雨欣第 4 章 有向符号图下离散多智能体系统的事件触发二分一致性所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。