读书笔记：Algorithms for Decision Making

上一篇 读书笔记：Algorithms for Decision Making（7）
下一篇 读书笔记：Algorithms for Decision Making（9）

三、模型不确定性（1）

解决存在模型不确定性的此类问题是强化学习领域的主题，这是这部分的重点。解决模型不确定性的几个挑战：首先，智能体必须仔细平衡环境探索和利用通过经验获得的知识。第二，在做出重要决策后很长时间内，可能会收到奖励，因此必须将以后奖励的学分分配给以前的决策。第三，智能体必须从有限的经验中进行概括。

1. Exploration and Exploitation

exploration of the environment with exploitation of knowledge

1.1 Bandit Problems

最简单的建模单臂老虎机问题（ one-armed bandits ），实际中的问题一般建模为多臂老虎机问题（multiarmed bandit problems）。

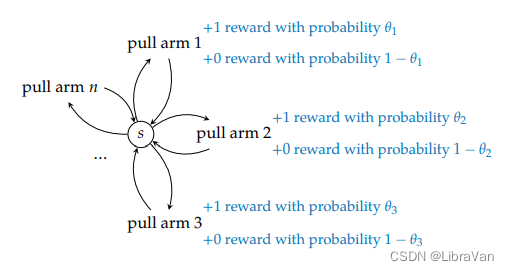
如果考虑一个简化的多臂老虎机问题，即每一个臂在做决策时给出一个二元结果。这样的问题可以看作一个$h$步，一状态，$n$ 行动且具有随机回报的MDP（马尔可夫决策问题）。

struct BanditProblem
	θ # vector of payoff probabilities
	R # reward sampler
end

function BanditProblem(θ)
	R(a) = rand() < θ[a] ? 1 : 0
	return BanditProblem(θ, R)
end

function simulate(????::BanditProblem, model, π, h)
	for i in 1:h
		a = π(model)
		r = ????.R(a)
		update!(model, a, r)
	end
end

1.2 贝叶斯模型估计

在贝叶斯推断中，Beta分布是Bernoulli、二项分布、负二项分布和几何分布的共轭先验分布。在此处，将其视为臂成功概率的先验分布，进而进行模型估计。

struct BanditModel
	B # vector of beta distributions
end

function update!(model::BanditModel, a, r)
	α, β = StatsBase.params(model.B[a])
	model.B[a] = Beta(α + r, β + (1-r))
	return model
end

1.3 Exploration 策略

• 不定向Exploration 策略：该策略中，不使用之前的输出信息指导非贪婪行动对环境的exploration。
  • $ϵ$-greedy exploration：以$ϵ$概率选择一条随机臂，或者选择一条先验概率最大的贪婪臂。

  mutable struct EpsilonGreedyExploration
  	ϵ # probability of random arm
  end
  
  function (π::EpsilonGreedyExploration)(model::BanditModel)
  	if rand() < π.ϵ
  		return rand(eachindex(model.B))
  	else
  		return argmax(mean.(model.B))
  	end
  end
  

  • explore-then-commit exploration：对前$k$个时间步均匀随机选择动作，然后选择贪婪行动。

  mutable struct ExploreThenCommitExploration
  	k # pulls remaining until commitment
  end
  
  function (π::ExploreThenCommitExploration)(model::BanditModel)
  	if π.k > 0
  		π.k -= 1
  		return rand(eachindex(model.B))
  	end
  	return argmax(mean.(model.B))
  end
  

• 定向Exploration 策略
  • softmax 策略

  mutable struct SoftmaxExploration
  	λ # precision parameter
  	α # precision factor
  end
  
  function (π::SoftmaxExploration)(model::BanditModel)
  	weights = exp.(π.λ * mean.(model.B))
  	π.λ *= π.α
  	return rand(Categorical(normalize(weights, 1)))
  end
  

  • optimism under uncertainty

  mutable struct QuantileExploration
  	α # quantile (e.g., 0.95)
  end
  
  function (π::QuantileExploration)(model::BanditModel)
  	return argmax([quantile(B, π.α) for B in model.B])
  end
  

  • UCB1 exploration

  mutable struct UCB1Exploration
  	c # exploration constant
  end
  
  function bonus(π::UCB1Exploration, B, a)
  	N = sum(b.α + b.β for b in B)
  	Na = B[a].α + B[a].β
  	return π.c * sqrt(log(N)/Na)
  end
  
  function (π::UCB1Exploration)(model::BanditModel)
  	B = model.B
  	ρ = mean.(B)
  	u = ρ .+ [bonus(π, B, a) for a in eachindex(B)]
  	return argmax(u)
  end
  

  • posterior sampling/randomized probability matching/Thompson sampling

  struct PosteriorSamplingExploration 
  end
  
  (π::PosteriorSamplingExploration)(model::BanditModel) = argmax(rand.(model.B))
  

• 最优Exploration 策略：与臂a相关的beta分布的参数表示为$(w_1,{\ell }_1)$，最优效用函数与最优策略可根据期望回报表示为$$\begin{array}{rl}{\mathcal{U}}^{\ast }(w_1,{\ell }_1,\cdots ,w_n,{\ell }_n)& =\underset{a}{\max }{Q}^{\ast }(w_1,{\ell }_1,\cdots ,w_n,{\ell }_n,a),\\ {\pi }^{\ast }(w_1,{\ell }_1,\cdots ,w_n,{\ell }_n)& =\underset{a}{\mathrm{argmax}}{Q}^{\ast }(w_1,{\ell }_1,\cdots ,w_n,{\ell }_n,a).\end{array}$$

2. 基于模型的方法

本部分讨论了最大似然和贝叶斯法，通过与环境的交互来学习潜在的动态和回报。

2.1 最大似然法

最大似然法计算状态转换，记录收到的奖励金额以估计模型参数。该方法可用于生成价值函数估计，该估计与exploration策略一起生成行动。

记录转换计数$N(s,a,s^{\prime })$，表示在采取行动$a$时观察到从$s$到$s^{\prime }$转换的次数。给定这些转换计数，转换函数的最大似然估计为$$T(s^{\prime }\mid s,a)\approx \frac{N(s,a,s^{\prime })}{N(s,a)},$$此处$N(s,a)={\sum }_{s^{\prime }}N(s,a,s^{\prime })$。

奖励函数也可以估计。当收到奖励时，更新$\rho (s,a)$，即在状态$s$中采取行动$a$时获得的所有奖励的总和。奖励函数的最大似然估计值为平均奖励$$R(s,a)\approx \frac{\rho (s,a)}{N(s,a)}.$$

mutable struct MaximumLikelihoodMDP
	???? # state space (assumes 1:nstates)
	???? # action space (assumes 1:nactions)
	N # transition count N(s,a,s′)
	ρ # reward sum ρ(s, a)
	γ # discount
	U # value function
	planner
end

function lookahead(model::MaximumLikelihoodMDP, s, a)
	????, U, γ = model.????, model.U, model.γ
	n = sum(model.N[s,a,:])
	if n == 0
		return 0.0
	end
	r = model.ρ[s, a] / n
	T(s,a,s′) = model.N[s,a,s′] / n
	return r + γ * sum(T(s,a,s′)*U[s′] for s′ in ????)
end

function backup(model::MaximumLikelihoodMDP, U, s)
	return maximum(lookahead(model, s, a) for a in model.????)
end

function update!(model::MaximumLikelihoodMDP, s, a, r, s′)
	model.N[s,a,s′] += 1
	model.ρ[s,a] += r
	update!(model.planner, model, s, a, r, s′)
	return model
end

2.1.1 更新策略

struct FullUpdate end

function update!(planner::FullUpdate, model, s, a, r, s′)
	???? = MDP(model)
	U = solve(????).U
	copy!(model.U, U)
	return planner
end

struct RandomizedUpdate
	m # number of updates
end

function update!(planner::RandomizedUpdate, model, s, a, r, s′)
	U = model.U
	U[s] = backup(model, U, s)
	for i in 1:planner.m
		s = rand(model.????)
	U[s] = backup(model, U, s)
	end
	return planner
end

struct PrioritizedUpdate
	m # number of updates
	pq # priority queue
end

function update!(planner::PrioritizedUpdate, model, s)
	N, U, pq = model.N, model.U, planner.pq
	????, ???? = model.????, model.????
	u = U[s]
	U[s] = backup(model, U, s)
	for s⁻ in ????
		for a⁻ in ????
			n_sa = sum(N[s⁻,a⁻,s′] for s′ in ????)
			if n_sa > 0
				T = N[s⁻,a⁻,s] / n_sa
				priority = T * abs(U[s] - u)
				if priority > 0
					pq[s⁻] = max(get(pq, s⁻, 0.0), priority)
				end
			end
		end
	end
	return planner
end

function update!(planner::PrioritizedUpdate, model, s, a, r, s′)
	planner.pq[s] = Inf
	for i in 1:planner.m
		if isempty(planner.pq)
			break
		end
		update!(planner, model, dequeue!(planner.pq))
	end
	return planner
end

2.1.2 Exploration

例如上部分提到的方法，如下：

function (π::EpsilonGreedyExploration)(model, s)
	????, ϵ = model.????, π.ϵ
	if rand() < ϵ
		return rand(????)
	end
	Q(s,a) = lookahead(model, s, a)
	return argmax(a->Q(s,a), ????)
end

为了避免陷入局部探索，还可使用：

mutable struct RmaxMDP
	???? # state space (assumes 1:nstates)
	???? # action space (assumes 1:nactions)
	N # transition count N(s,a,s′)
	ρ # reward sum ρ(s, a)
	γ # discount
	U # value function
	planner
	m # count threshold
	rmax # maximum reward
end

function lookahead(model::RmaxMDP, s, a)
	????, U, γ = model.????, model.U, model.γ
	n = sum(model.N[s,a,:])
	if n < model.m
		return model.rmax / (1-γ)
	end
	r = model.ρ[s, a] / n
	T(s,a,s′) = model.N[s,a,s′] / n
	return r + γ * sum(T(s,a,s′)*U[s′] for s′ in ????)
end

function backup(model::RmaxMDP, U, s)
	return maximum(lookahead(model, s, a) for a in model.????)
end

function update!(model::RmaxMDP, s, a, r, s′)
	model.N[s,a,s′] += 1
	model.ρ[s,a] += r
	update!(model.planner, model, s, a, r, s′)
	return model
end

function MDP(model::RmaxMDP)
	N, ρ, ????, ????, γ = model.N, model.ρ, model.????, model.????, model.γ
	T, R, m, rmax = similar(N), similar(ρ), model.m, model.rmax
	for s in ????
		for a in ????
			n = sum(N[s,a,:])
			if n < m
				T[s,a,:] .= 0.0
				T[s,a,s] = 1.0
				R[s,a] = rmax
			else
				T[s,a,:] = N[s,a,:] / n
				R[s,a] = ρ[s,a] / n
			end
		end
	end
	return MDP(T, R, γ)
end

2.2 贝叶斯法

贝叶斯法计算模型参数的后验分布，通过后验采样获得合理的近似值。

mutable struct BayesianMDP
	???? # state space (assumes 1:nstates)
	???? # action space (assumes 1:nactions)
	D # Dirichlet distributions D[s,a]
	R # reward function as matrix (not estimated)
	γ # discount
	U # value function
	planner
end

function lookahead(model::BayesianMDP, s, a)
	????, U, γ = model.????, model.U, model.γ
	n = sum(model.D[s,a].alpha)
	if n == 0
		return 0.0
	end
	r = model.R(s,a)
	T(s,a,s′) = model.D[s,a].alpha[s′] / n
	return r + γ * sum(T(s,a,s′)*U[s′] for s′ in ????)
end

function update!(model::BayesianMDP, s, a, r, s′)
	α = model.D[s,a].alpha
	α[s′] += 1
	model.D[s,a] = Dirichlet(α)
	update!(model.planner, model, s, a, r, s′)
	return model
end

2.2.1 贝叶斯自适应马尔可夫决策过程

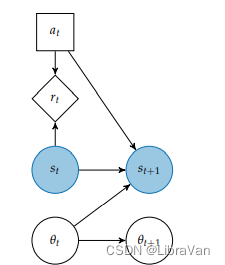
将具有未知模型的MDP中的最优行为问题表述为具有已知模型的高维MDP，该MDP被称为贝叶斯自适应马尔可夫决策过程。

状态空间表示为$\mathcal{S}\times \mathcal{B}$，其中$\mathcal{B}$是模型参数$\theta$的可能置信空间。在每次迭代过程中的$s\to (s,b)$。

2.2.2 后验采样

struct PosteriorSamplingUpdate end

function Base.rand(model::BayesianMDP)
	????, ???? = model.????, model.????
	T = zeros(length(????), length(????), length(????))
	for s in ????
		for a in ????
			T[s,a,:] = rand(model.D[s,a])
		end
	end
	return MDP(T, model.R, model.γ)
end

function update!(planner::PosteriorSamplingUpdate, model, s, a, r, s′)
	???? = rand(model)
	U = solve(????).U
	copy!(model.U, U)
end

后验采样通过求解从置信状态采样的MDP，而不是推理所有可能的MDP来降低求解Bayes自适应MDP的高计算复杂性。

最后

以上就是听话鸵鸟为你收集整理的读书笔记：Algorithms for Decision Making（8）读书笔记：Algorithms for Decision Making三、模型不确定性（1）的全部内容，希望文章能够帮你解决读书笔记：Algorithms for Decision Making（8）读书笔记：Algorithms for Decision Making三、模型不确定性（1）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。