概述
我们知道电路在高速工作时，器件的寄生电容和负载电容是不能被忽视的，所以对电路的频率特性研究必不可少。
放大器特别是多级放大器在工作时，稳定性和频率补偿是必须要考虑的。在分析放大器的频率特性之前我们需要具备几个基本知识。如果你已经熟知密勒定理以及反馈系统稳定性和波特图，可以直接跳过这一节。
1、密勒定理
如图1中的电路（a）可以转换为图（b）中的电路，则
其中
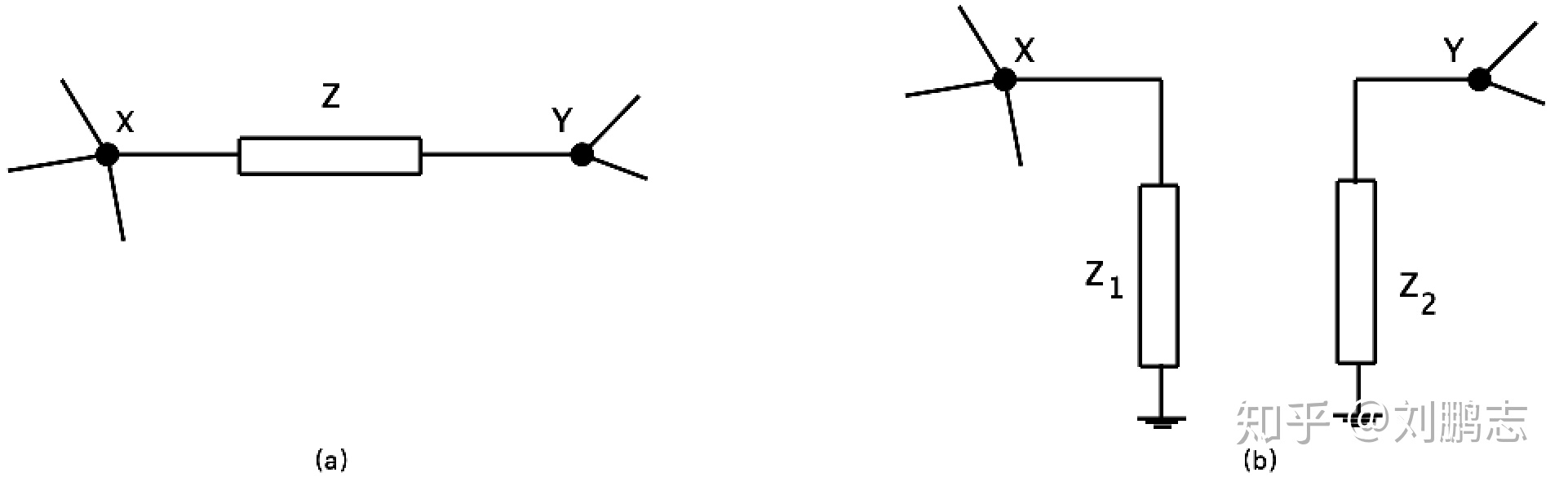
例如，图2假设理想放大器的放大倍数是-A，不考虑其他寄生参数，则跨接在输入输出两端的电容
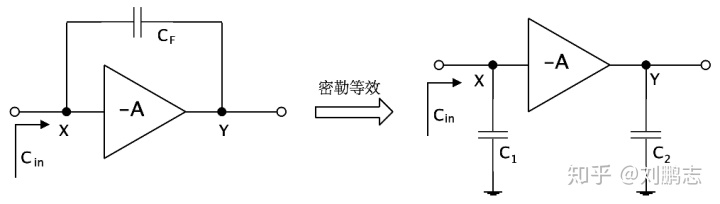
2、反馈系统的稳定性和补偿
图3显示了一个负反馈系统，则该系统的闭环函数可写为：
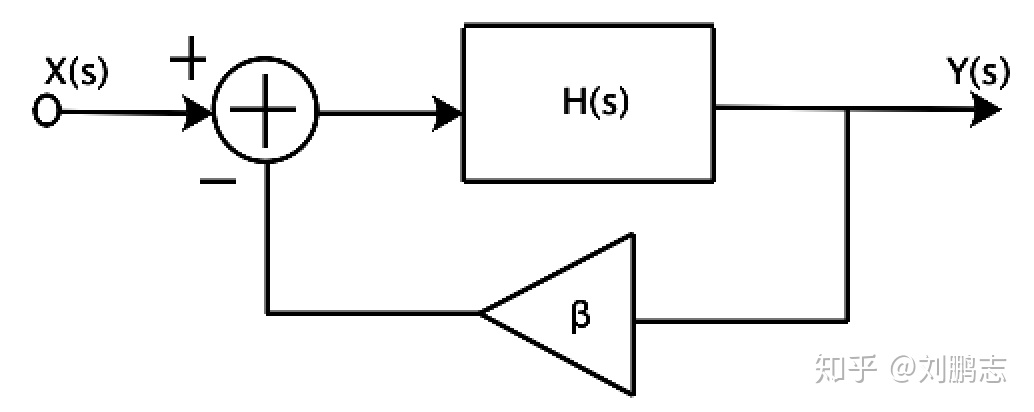
其中
从图4中显示了不稳定系统和稳定系统的波特图：
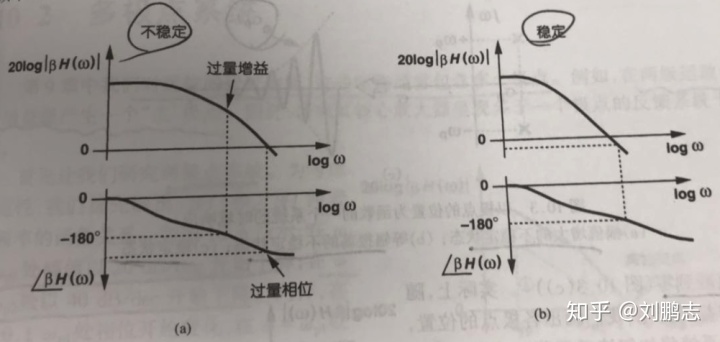
在波特图中：
相位的变化——每个极点最多贡献90°的相移，约在每个极点的0.1倍处开始下降，单极点系统（稳定）中，在极点处相移为45°。
幅值的变化——反馈系数
我们知道，要想保证系统稳定，
相位裕度（Phase Margin，PM）——定义为
对于多极点系统，我们需要对系统进行频率补偿，使闭环电路稳定。通常有两种方法：
（1）把总的相移减至最小，使相位交点往外推。（意味着要减小极点，即减小放大器的级数）
（2）降低增益，使增益交点往里推。（将主极点往里推）
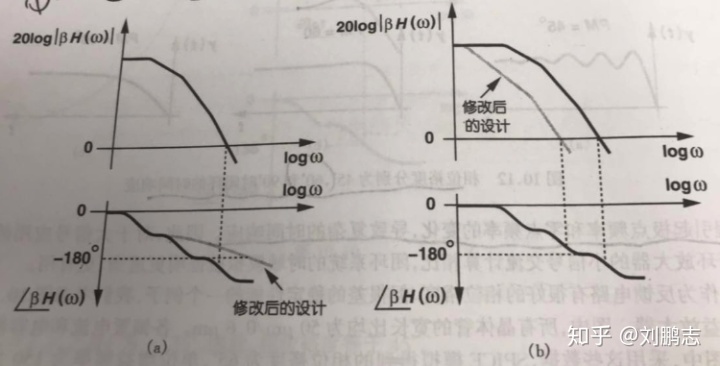
事实上，实际的运放设计过程中，在满足要求的情况下，我们首先把运放的极点数减至最小。由于这样得到的电路仍有可能不具有足够的相位裕度，则我们要对运放进行补偿，即修改设计，以使增益交点向原点移动。
最后
以上就是超帅唇彩为你收集整理的matlab求传递函数在某个频率点的增益_放大器频率特性（一）的全部内容，希望文章能够帮你解决matlab求传递函数在某个频率点的增益_放大器频率特性（一）所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复