- 基本逻辑
- 复合逻辑
- 拓展知识
1. 基本逻辑
基本逻辑运算:
-
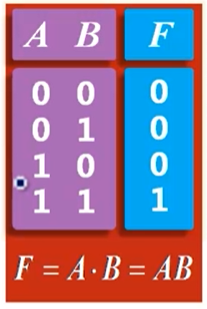
与: 一个逻辑命题的所有条件(输入)同时成立时,结论(输出)才成立
-
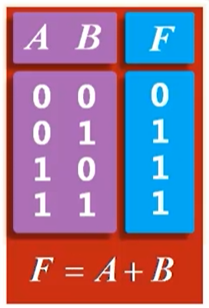
或: 一个逻辑命题的所有条件(输入)中,只要有一个成立,结论(输出)就成立
-
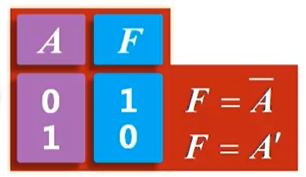
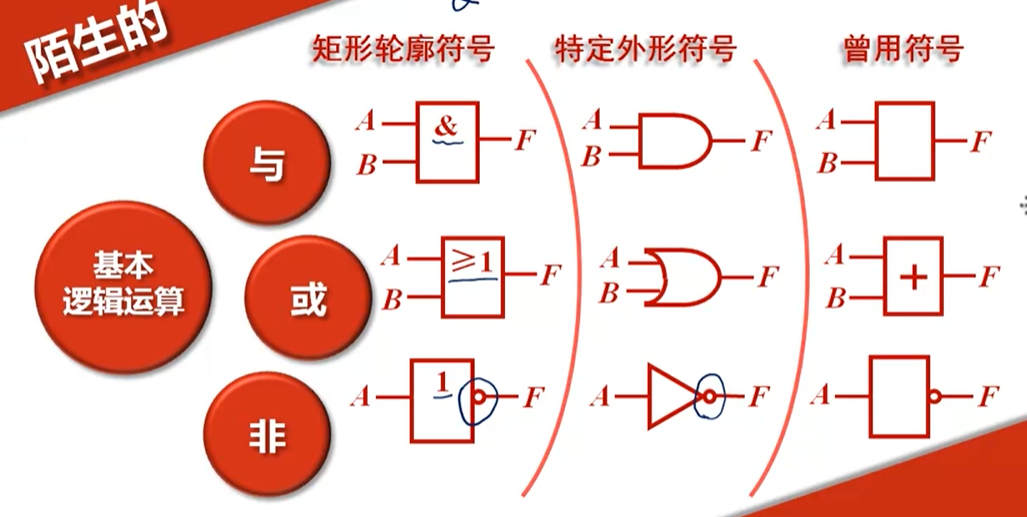
非: 逻辑命题的条件不成立时,结论必成立;条件成立时,结论必不成立
2. 复合逻辑
2.1与非
逻辑表达式:

逻辑门符号:
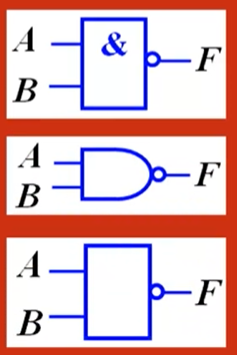
真值表:
| A | B | F |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
即见0得1,全1得0
2.2或非
逻辑表达式:
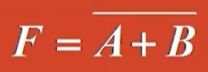
逻辑门符号:
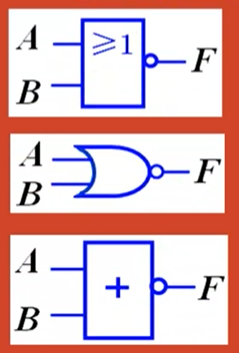
真值表:
| A | B | F |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
即见1得0,全0得1
2.3与或非
逻辑表达式:

逻辑门符号:
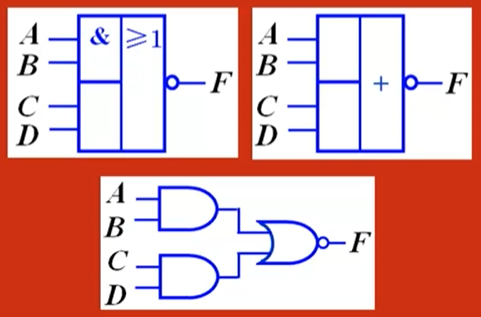
真值表:
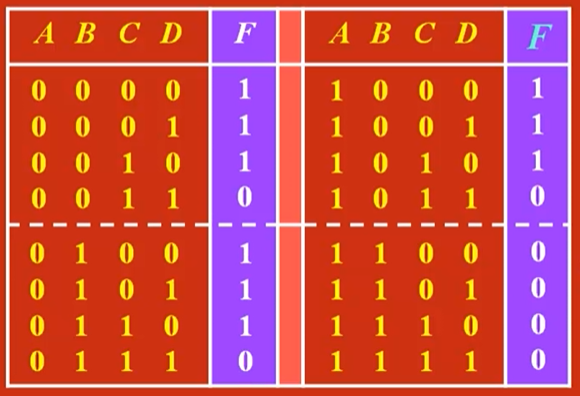
2.4 异或 和 同或
表达式:
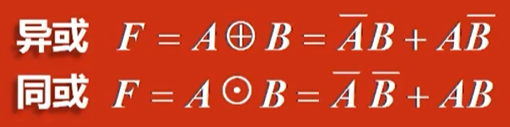
名称:
- 异或也叫“模2加”运算(加法器)
- 同或也叫"符合"逻辑,有时也叫“异或非”(数值比较器)
功能:
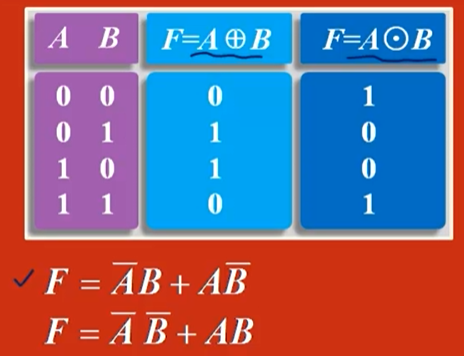
-
两输入异或:
输入取值相异,输出为1;取值相同,输出为0 -
两输入同或:
输入取值相同,输出为1;取值相异,输出为0。
逻辑门符号:
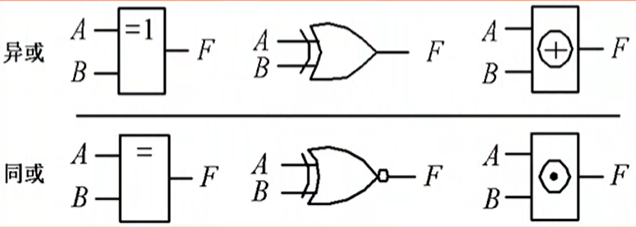
同或 即 异或非
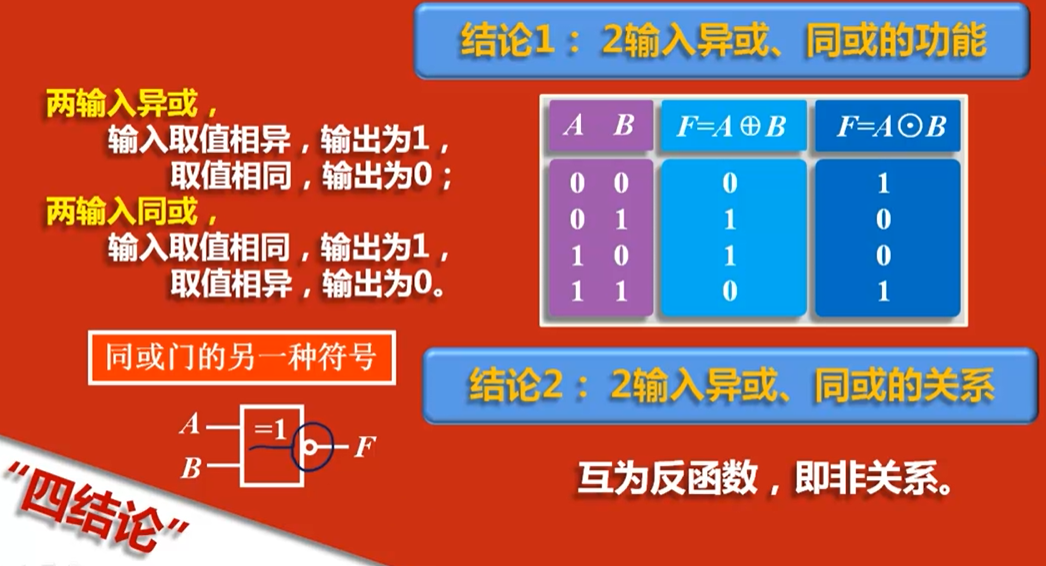
- 结论1:两输入异或、同或的功能
- 两输入异或,输入取值相异,输出为1,取值相同,输出为0;
- 两输入同或,输入取值相同,输出为1,取值相异,输出为0。
- 结论2:两输入异或、同或的关系
- 两输入异或、同或互为反函数,即非关系。
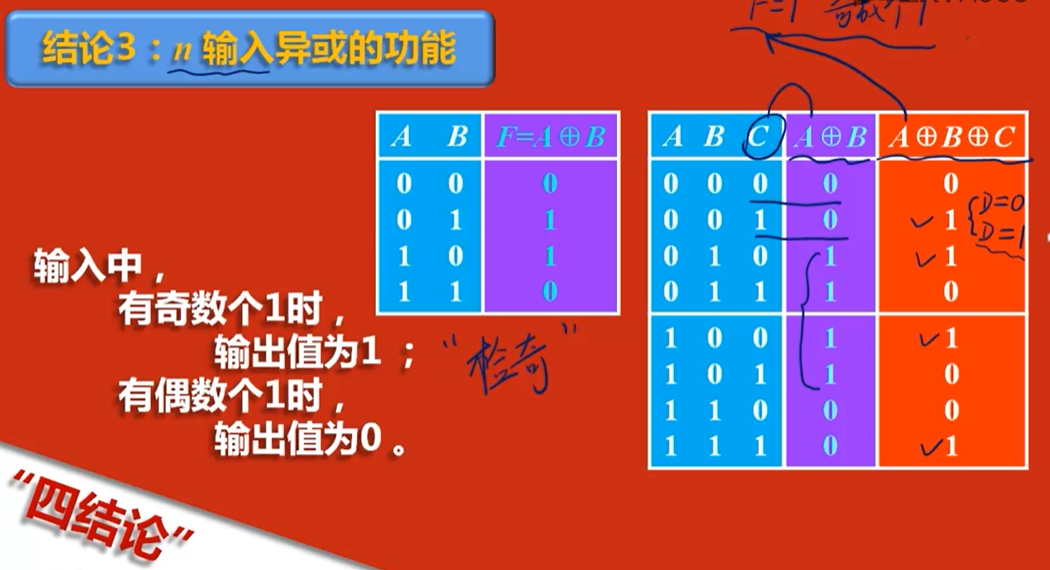
- 结论3: n输入异或的功能
- 输入中,有奇数个1时,输出值为1;有偶数个1时,输出值为0。
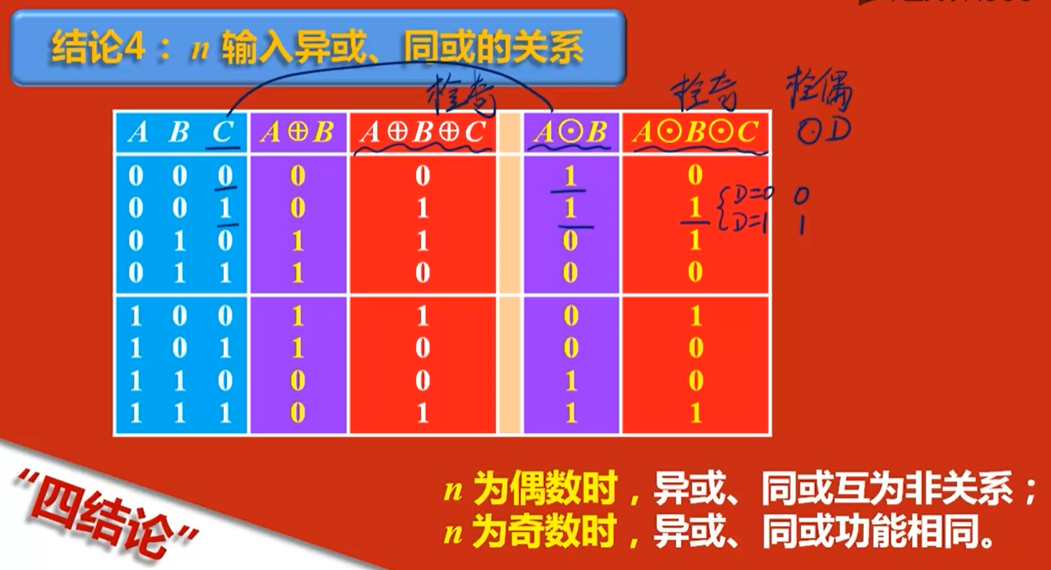
- 结论4: n输入异或、同或的关系
- n为偶数时,异或、同或互为非关系;
- n为奇数时,异或、同或功能相同。
3. 拓展知识
奇偶校验码的生成与检测
- 所谓“奇校验码”,指信息位和校验位中“1”的个数为奇数;
- 所谓“偶校验码”,指信息位和校验位中,“1”的个数为偶数。
奇偶校验码的生成,指的是依据信息位中1的个数,按校验规则产生校验位具体的取值。奇偶校验码的检测,指的是接收端收到具体代码后,计算整个码组中1的个数,验证是否符合校验规则,由此判断是否产生了误码
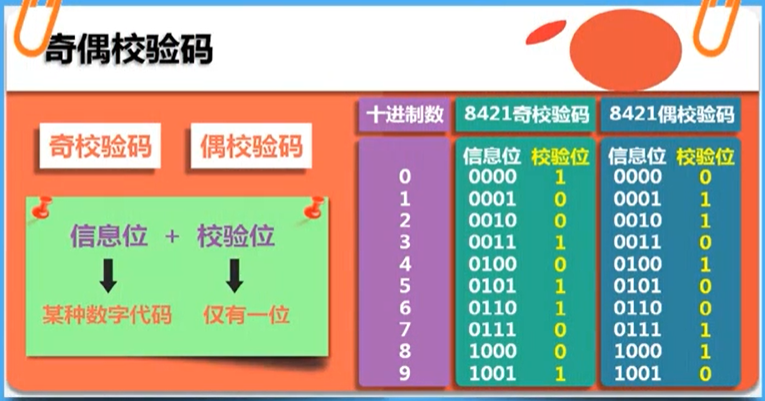
奇偶校验码的生成:
依据信息位中1的个数,按校验规则产生校验位具体的取值。
奇偶校验码的检测:
收到具体代码后,计算整个码组中1的个数,验证是否符合校验规则,由此判断是否产生了误码。
偶校验码的生成:
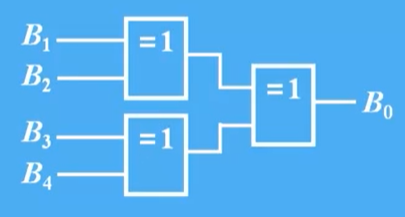
以8421偶校验码为例,设一个码组中的五位码元从高到低依次为:
- 信息位B4、 B3、B2、B1
- 校验位B0
8421偶校验码的生成电路如图所示。将满足8421码规则的四位信息位B4、B3、B2、B1作为四输入异或逻辑电路的输入变量,则根据n输入异或的功能,当信息位中1的个数为奇数时,输出B。为1,信息位中1的个数为偶数时,输出B0为0
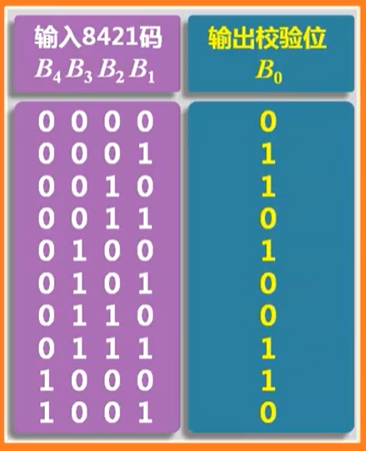
得到输出B0后,再将五位码元B4、B3、 B2、 B1、 B0并行输出,则1的个数必为偶数,由此形成了8421偶校验码
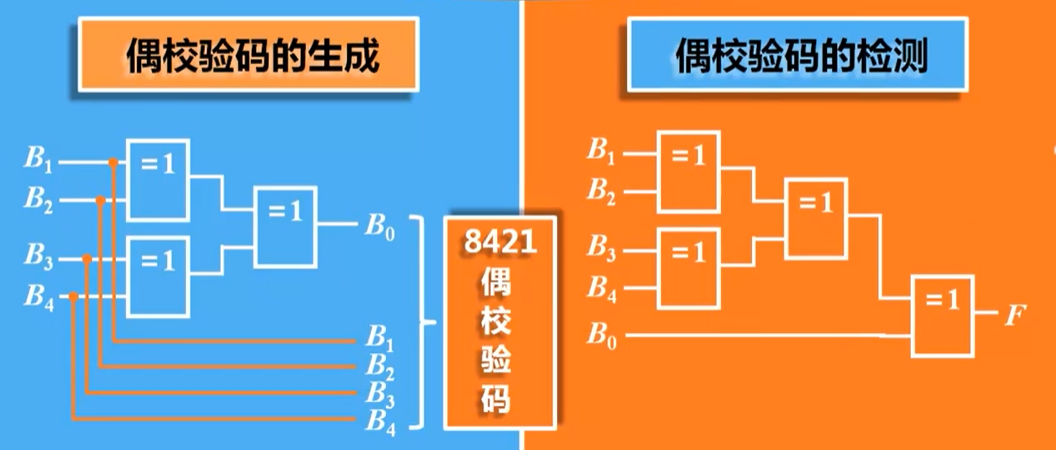
偶校验码的检测:
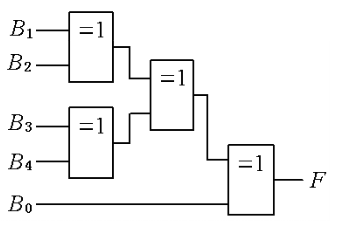
在接收端,将收到的8421偶校验码的五位码元B4、B3、B2、B1、B0作为五输入异或逻辑电路的输入,输出F为检测信号
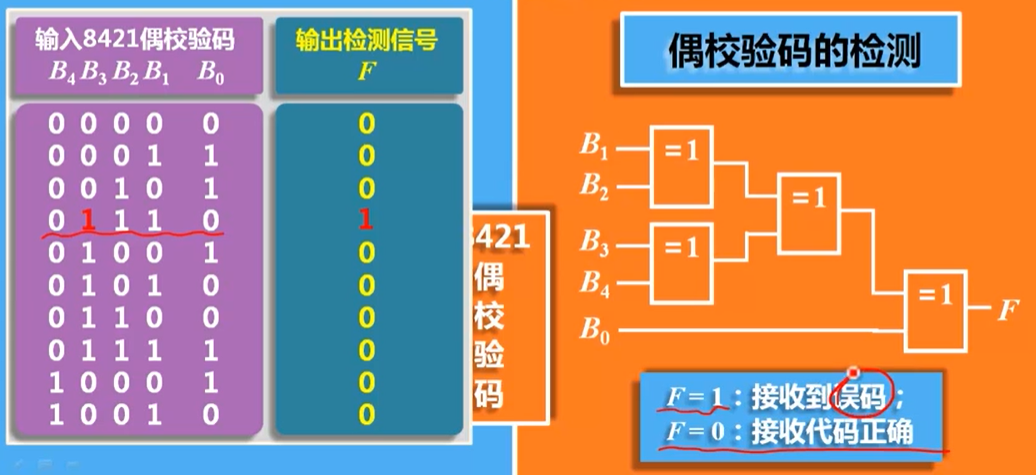
根据n输入异或的功能,五位码元中,1的个数为偶数时,输出F为0;1的个数为奇数时,输出F为1
最后
以上就是过时可乐最近收集整理的关于数字电子技术之基本逻辑运算与常用复合逻辑的全部内容,更多相关数字电子技术之基本逻辑运算与常用复合逻辑内容请搜索靠谱客的其他文章。








发表评论 取消回复