摘要:本节介绍用于分析数字电路逻辑功能的数学方法——逻辑代数。首先将介绍逻辑代数的基本公式、常用公式和几个重要的定理,然后讲授逻辑代数的各种描述方法以及这些描述方法之间的相互转换。最后。介绍逻辑代数的化解方法。
基本概念
逻辑:在这里指事物的因果关系。
二值逻辑:只有两种对立逻辑状态的逻辑关系称为二值逻辑。
逻辑运算:当两个二进制数码表示不同的逻辑状态时,它们之间可以按照指定的某种因果关系进行推理运算。
布尔代数:1849年英国数学家乔治布尔首先提出了进行逻辑运算的数学方法——布尔代数。后来也称为开关代数或逻辑代数。
逻辑变量:逻辑代数中变量也用字母表示,这种变量被称为逻辑变量。
三种基本运算
与(AND):只有决定事物结果的全部条件同时具备时,结果才会发生。
或(OR):在决定事物结果的诸条件中只要有任一条件满足,结果就会发生。
非(NOT):只要条件具备了,结果便不会发生;而条件不具备是,结果一定发生。
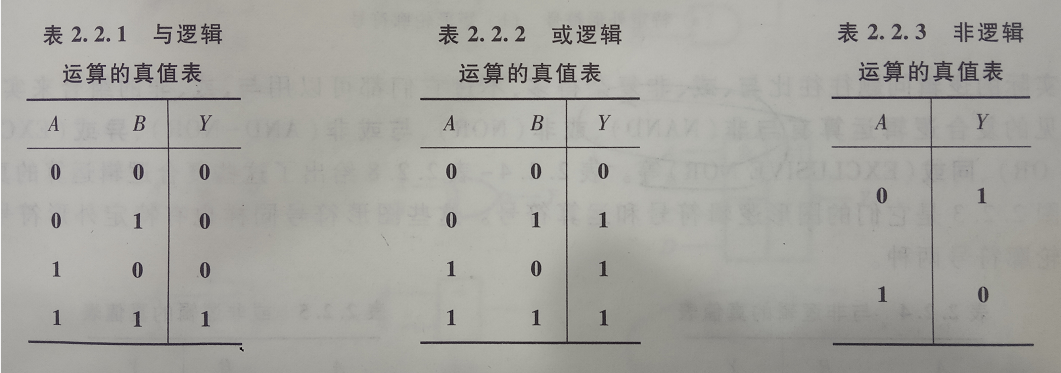
在逻辑代数中,将与、或、非看作是逻辑变量A、B间的三种最基本的逻辑运算,并以“ ”表示与运算。以“ + ”表示或运算。以变量右上角的“ ' ”表示非运算。
同时将实现与逻辑运算的单元电路称为与门,将实现或逻辑运算的单元电路称为或门,将实现非逻辑运算的单元电路称为非门(也称之为反相器)。实际的逻辑问题往往比与、或、非复杂的多,不过他们都可以用与、或、非的组合来实现。最常见的复合逻辑运算有与非、或非、与或非、异或、同或等。
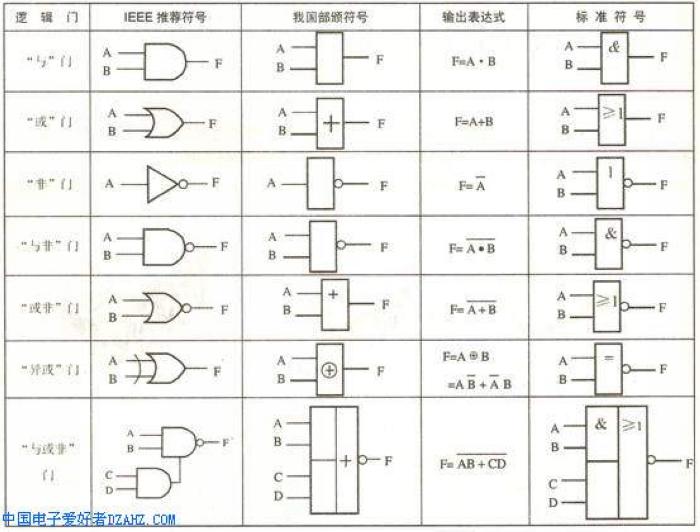
逻辑代数公式
下表给出了逻辑代数的基本公式,这些公式也称为布尔恒等式。
| 序号 | 公式 | |
|---|---|---|
| 1 | 变量与常量运算规则 | |
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | 重叠律 | |
| 6 | ||
| 7 | 互补律 | |
| 8 | ||
| 9 | 交换律 | |
| 10 | ||
| 11 | 结合律 | |
| 12 | ||
| 13 | 分配律 | |
| 14 | ||
| 15 | 反演律 | |
| 16 | ||
| 17 | 还原律 | |
| 18 |
下表列出来几个常用公式,这些公式可由基本公式推导出。
| 序号 | 公式 |
|---|---|
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 |
逻辑代数基础定理
代入定理:在任何一个包含变量A的逻辑等式中,若以另外一个逻辑式代入式中所有A的位置,则等式仍然成立。
反演定理:对于任何一个逻辑式,若将其中所有的“
”换成“ + ”,“ + ”换成“
”,0换成1,1换成0,原变量换成反变量,反变量换成原变量,则得到的结果就是
。
对偶定理:若两个逻辑式相等,则它们的对偶式也相等。对于任何一个逻辑式,若将其中的“
”换成“ + ”,“ + ”换成“
”,0换成1,1换成0,则得到一个新的逻辑式
,这个
就称为
的对偶式,或者说
和
互为对偶式。
逻辑函数及其描述方法
逻辑函数:如果以逻辑变量作为输入,以运算结果作为输出,那么当输入变量的取值确定后,输出的取值也随之确定。因此,输入与输出之间乃是一种函数关系。这种函数关系称为逻辑函数,写作
描述方法:逻辑真值表、逻辑函数式、逻辑图、波形图(时序图)、卡诺图、硬件描述语言等。
逻辑函数的标准形式
最小项:在n变量逻辑函数中,若m为包含n个因子的乘积项,而且这n个变量均以原变量或反变量的形式在m中出现一次,则称m为该组变量的最小项。
最大项:在n变量逻辑函数中,若M为n个变量之和,而且这n个变量均以原变量或反变量的形式在M中出现一次,则称M为该组变量的最大项。
逻辑函数最小项之和形式:首先将给定的逻辑函数式化为若干乘积项之和的形式。然后,再利用基本公式将每个乘积项中缺少的因子补全。这样就可以将与或的形式化为最小项之和的标准形式。
逻辑函数最大项之积形式:利用逻辑代数的基本公式和定理,首先我们一定能把任何一个逻辑函数式化成若干多项式相乘的或与形式。然后再利用基本公式将每个多项式中缺少的变量补全,就可以将函数式的或与形式化成最大项之积的形式。
逻辑函数的化解方法
公式化解法:并项法、吸收法,消项法、消因子法、配项法。
卡诺图化解法:合并最小项(若两个最小项相邻,则可合并为一项并消去一对因子。合并后的结果只剩下公共因子。)
Q-M法:
卡洛图法化简虽然比较直观,简单,但是也有自身的缺点,如当逻辑变量大于五个之后,会变得很困难。而公式法化简虽然虽然不受变量数量的影响,但是化简过程并没有固定、通用的步骤。所以也很难借助计算机辅助进行化简。
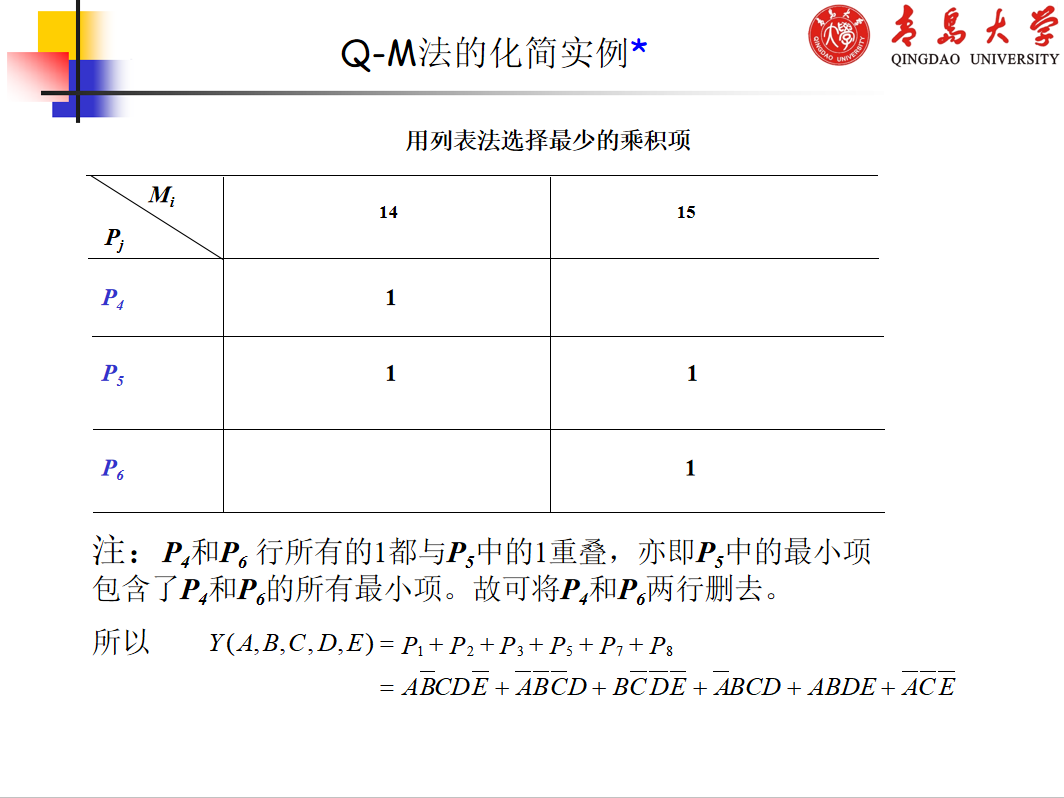
由奎恩(W.V.Quine)和麦克拉斯基(E.J.McCluskey)提出的用列表方式进行化简的方法,克服 了公式化简法和卡诺图化简法的的局限性,它有确定的流程,适用于任何复杂逻辑函数的化简,因此 适用于编制计算机辅助化简程序。通常将这种化简方法称为奎恩-麦克拉斯基化简法,简称Q-M法。
Q-M法的基本原理仍然是通过合并相邻小项并消去多余因子而求得逻辑函数的简与或式。 下面结合一个具体的例子简要介绍Q-M法的基本原理和化简步骤。(如果理解困难请参阅《数字电子技术基础》(第六版)2.6小节)

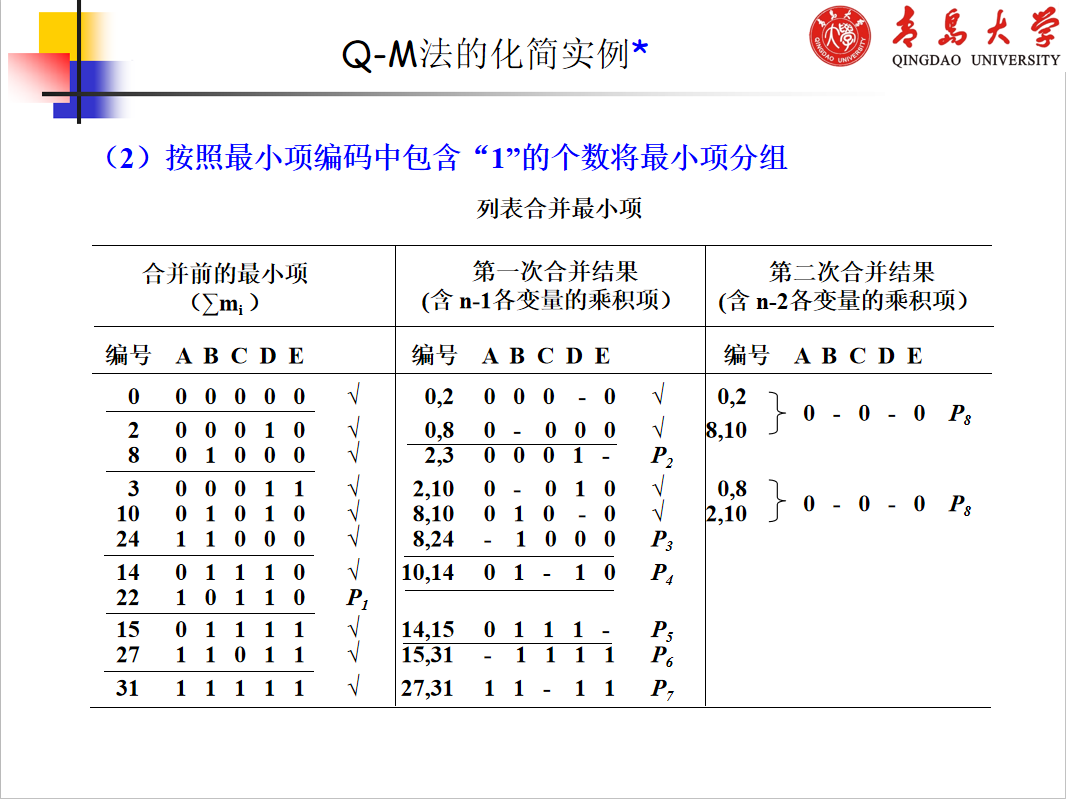
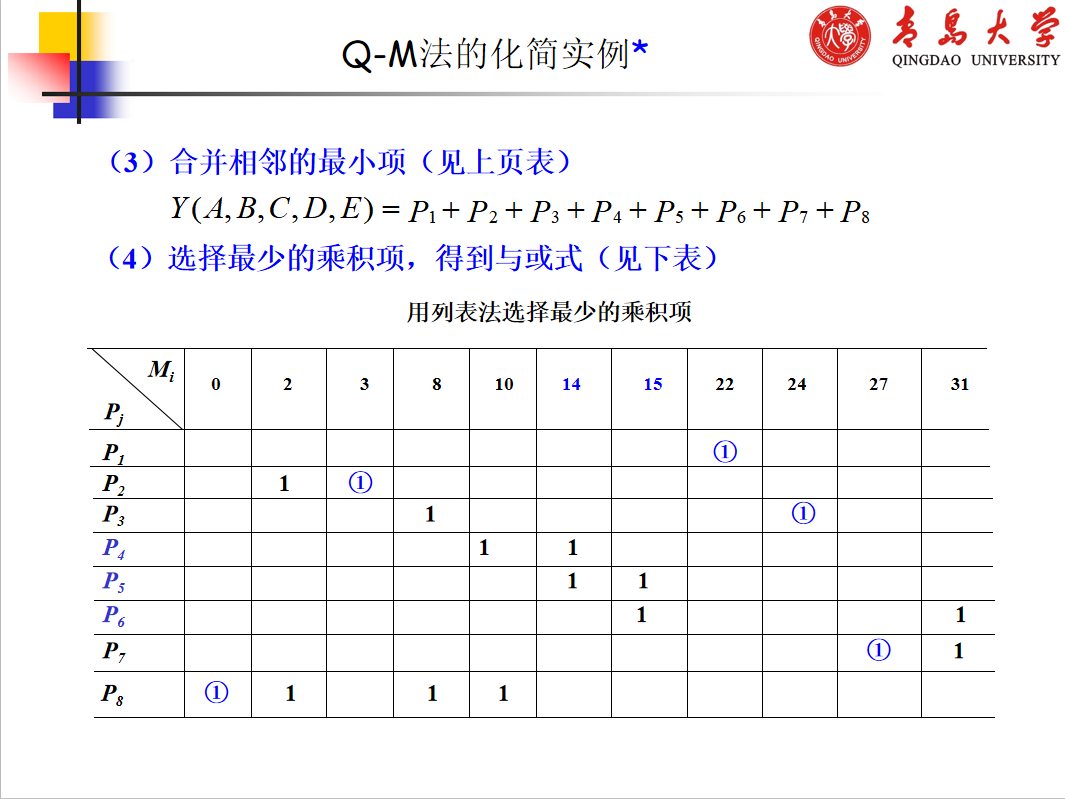
无关项的化解:略
多输出逻辑函数的化解:略
参考链接
- 《数字电子技术基础》(第六版)高等教育出版社
最后
以上就是苹果小甜瓜最近收集整理的关于数字电路-逻辑代数基础的全部内容,更多相关数字电路-逻辑代数基础内容请搜索靠谱客的其他文章。








发表评论 取消回复