四元数与欧拉角之间的转换
在3D图形学中,最常用的旋转表示方法便是四元数和欧拉角,比起矩阵来具有节省存储空间和方便插值的优点。本文主要归纳了两种表达方式的转换,计算公式采用3D笛卡尔坐标系:
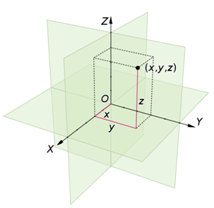
图1 3D Cartesian coordinate System (from wikipedia)
定义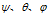 分别为绕Z轴、Y轴、X轴的旋转角度,如果用Tait-Bryan angle表示,分别为Yaw、Pitch、Roll。
分别为绕Z轴、Y轴、X轴的旋转角度,如果用Tait-Bryan angle表示,分别为Yaw、Pitch、Roll。
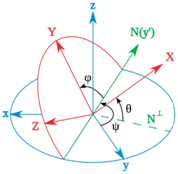
图2 Tait-Bryan angles (from wikipedia)
一、四元数的定义
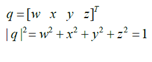
通过旋转轴和绕该轴旋转的角度可以构造一个四元数:
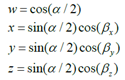
其中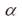 是绕旋转轴旋转的角度,
是绕旋转轴旋转的角度,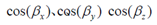 为旋转轴在x,y,z方向的分量(由此确定了旋转轴)。
为旋转轴在x,y,z方向的分量(由此确定了旋转轴)。
二、欧拉角到四元数的转换
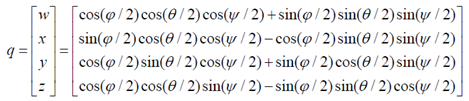
三、四元数到欧拉角的转换

arctan和arcsin的结果是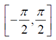 ,这并不能覆盖所有朝向(对于
,这并不能覆盖所有朝向(对于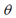 角
角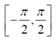 的取值范围已经满足),因此需要用atan2来代替arctan。
的取值范围已经满足),因此需要用atan2来代替arctan。
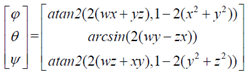
四、在其他坐标系下使用
在其他坐标系下,需根据坐标轴的定义,调整一下以上公式。如在Direct3D中,笛卡尔坐标系的X轴变为Z轴,Y轴变为X轴,Z轴变为Y轴(无需考虑方向)。
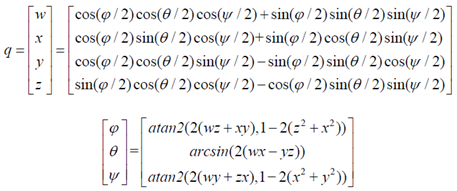
五、示例代码
http://www.cppblog.com/Files/heath/Euler2Quaternion.rar
Demo渲染两个模型,左边使用欧拉角,右边使用四元数,方向键Up、Left、Right旋转模型。
最后
以上就是落寞时光最近收集整理的关于四元数与欧拉教的转换权威材料的全部内容,更多相关四元数与欧拉教内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复