红包分配算法（年后写的）

110 阅读 0 评论 73 点赞

我是靠谱客的博主怡然飞鸟，最近开发中收集的这篇文章主要介绍红包分配算法（年后写的），觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

今天正月十一，春节已经过去了10天，红包想必大家都已经抢很多了，不知道大家有没有想过这个红包怎么实现分配的呢？

为什么有的人分这么多，有的人分那么多？

到底是怎么实现的呢?

答案是，我也不知道。

现在最火的就是微信红包了，当然我们也不可能知道微信红包究竟采用了什么样的具体算法，只能通过观察和分析，加上网络上的众人之力，给出一个可能的红包分配方案，红包随机分配算法可以很简单，也可以很复杂，下面就从简入难着手，力图实现一个靠谱的红包随机分配算法版本。

简单的开始

先简化问题：红包总金额为money，红包个数为n，求各个红包的金额，代码如下：

def redPacketsRandom(money, n):
    divide_table = []
    for i in range(0,n):
        divide_table.append(random.uniform(1,10))
    sum_ = sum(divide_table)
    result = []
    cur_sum = 0.0
    for i in range(0,n-1)：
        cur = round((divide_table[i]*money/sum_),2)
        result.append(cur)
        cur_sum = cur_sum + cur
    result.append(money-cur_sum)
    return result

代码很简单，但是有几个重要细节需要说明：

1.利用random生成随机数时，要避免生成的随机数中存在负数和0，如果有0的话该红包将为控红包，显然是不行，因此，上面代码中将随机数固定在1-10的范围内。

2.最后每个红包的金额数都要精确到小数点后两位，对应上述代码中的：cur = round((divide_table[i]*money/sum_),2)。这样做有两个原因是小数点后3位的钱没有意义。

3，计算最后一个红包的金额时，要用总金额减去前面红包的金额总和，而不能跟前面的红包金额计算方法一样（根据比例来算），这是因为之前精确到小数点后两位的操作可能造成精度的丢失，而使最后所有红包的金额总和略小于money的值。其实，及时在前面没有进行青雀到小数点后两位的操作，也同样可能造成精度的丢失，因为编程语言智能存储有限长度的浮点数，当遇到小数点后的位数较多甚至是无限小数的时候，还是会自动丢失后面的值。

总之，在这个最简单的版本里，仿佛也能看到程序员的修养。

红包金额满足固定分布

很高兴网络上有不少童鞋跟我一样对红包的分配算法很感兴趣，并且对此神佑研究。这也让我写这篇博文的时候省了很多事儿，我选择了站在巨人的甲板上，例如，之湖上就有人专门对此提问：微信红包金额分配的算法是怎样的？谁比较容易到最佳手气？谁有机会拿到较大的金额？问题下面有很多有意义的回答，其中知乎用户“马景铖”的回答最为详细。他认为“钱包钱数满足截尾正态随机数分布”，并给出了自己的调研数据。

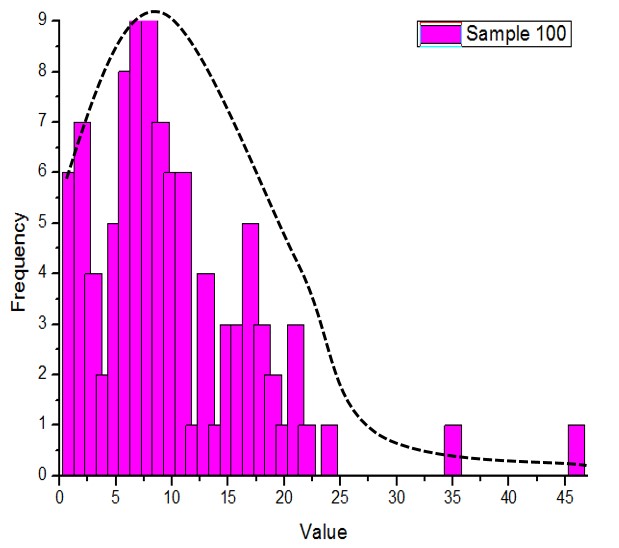
当然，我不能保证这一结论的正确性，因为我没有自己调研过真实数据，只是单纯地觉得他说的好像很有道理(^__^) 。说实话，即使我自己做过这样的调研，也不能保证调研结果的正确性，毕竟我所能调研的数据量不会很大。不过没有关系，这里暂且认为这是一个可靠的假设。下面的任务就是如何修改上面的代码，使钱包的金额满足这样的分布。下面给出参考代码（可以对比前面的代码，着眼于新增和修改的部分）：

def redPacketsRandom(money, n):
#指定均值和标准差,均值和标准差的指定方法不确定，这里只是给出一种可能
mu = float(money)/n
sigma = mu/2.0
divide_table = []
while len(divide_table) < n:
    random_float = random.normalvariate(mu, sigma)
    if random_float > 0:
        divide_table.append(random_float)
sum_ = sum(divide_table)
result = []
cur_sum = 0.0
for i in range(0,n-1):
    cur = round((divide_table[i]*money/sum_),2)
    result.append(cur)
    cur_sum = cur_sum + cur
result.append(money-cur_sum)
return result

越是后面的钱包，价值普遍越高

这一点非常有趣，而且经过多次观察确实如此。以前以为红包在于“抢”，即手速越快越好，但是其实开始抢到的往往都是小红包。这就要求抢红包的时候拿捏好尺度，太快了只能抢到小红包，太晚了红包则被抢完了，连小红包都没有。突然想说，人生就像抢红包，有些人愿意冒险一试，成功了建万事功勋，失败了一无所有；有些人则愿意作保底打算，稳妥为上。
切入正题，如果简单地将生成的红包列表按大小进行排序，依照严格的大小顺序从高往低出红包，肯定是不行的，因为小红包在前大红包在后只是一种总体上的统计规律，而不是严格的规则。也就是说，在后面领到小红包，以及在前面领到大红包，都是有可能的，只是可能性比较小而已。这个时候，就需要对出红包的顺序进行随机安排。参考代码如下：

def redPacketsRandom(money, n):
#指定均值和标准差,均值和标准差的指定方法不确定，这里只是给出一种可能
mu = float(money)/n
sigma = mu/2.0
divide_table = []
while len(divide_table) < n:
    random_float = random.normalvariate(mu, sigma)
    if random_float > 0:
        divide_table.append(random_float)
sum_ = sum(divide_table)
result = []
cur_sum = 0.0
for i in range(0,n-1):
    cur = round((divide_table[i]*money/sum_),2)
    result.append(cur)
    cur_sum = cur_sum + cur
result.append(money-cur_sum)
#确定出红包的顺序
result = sorted(result)
sort_dict = {}
for i in range(0,n):
    mu = i+1
    sigma = 2
    random_float = random.normalvariate(mu, sigma)
    sort_dict[i] = random_float
sort_dict = sorted(sort_dict.items(), key=lambda d: d[1])
result_sort = [0.0]*n
for i in range(0,n):
    result_sort[sort_dict[i][0]] = result[i]
return result_sort

这里对上面确定红包顺序的代码解释一下：
一开始，将求得的红包金额按照从小打到进行排序；其次，生成一个确定红包大小顺序的随机数序列，第一个随机数满足均值为1，标准差为2；第二个随机数满足均值为2.标准差为2；第三个随机数满足均值为3，标准差为2；……
；第n个随机数满足均值为n，标准差为2。这样，就构成了一个随机数序列，这个序列服从这样一个规律：前面的数的总体均值小于后面的数的总体均值。然后，将生成的随机数序列进行从小达到排序，排序的时候要保留该随机数在排序之前的下标。假设第三个随机数在所有随机数中最小，则说明第三个红包应该是所有红包中最小的红包，以此类推……