多元高斯分布模型

引子

在服务器运转监控的问题中，我们获得一个服务器样本 $x$ ，并且，计算了 $p(x_1;{\mu }_1,{\delta }_1^2)及p(x_2;{\mu }_2,{\delta }_2^2)$ ，认为该服务器的 CPU 负载和内存使用都在正常范围内，也就认为该服务器运转正常：

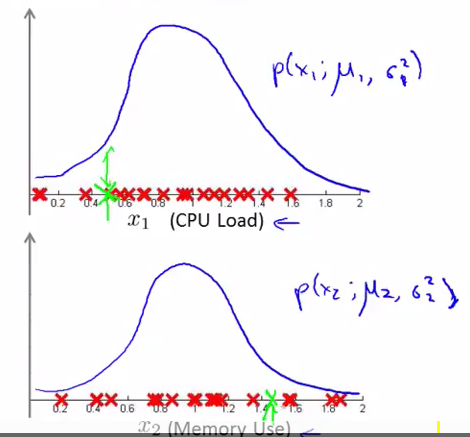
但是，截断边界却将该样本截在了正常样本之外，认为服务器发生异常：

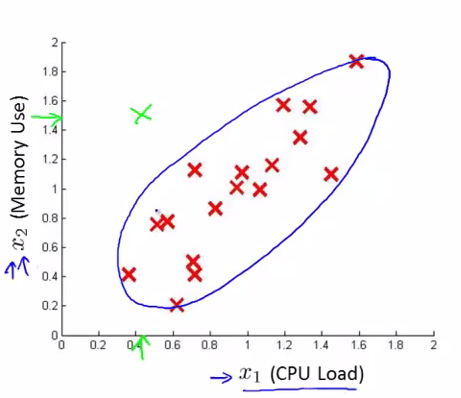
可以看到，出现错误截端的原因在于，我们的高斯分布模型形成的截断边界太固定。试想，如果我们原有的决策边界能经放缩，旋转等操作，变换到下图的紫色边界位置，该服务器就不会被错分为异常了：

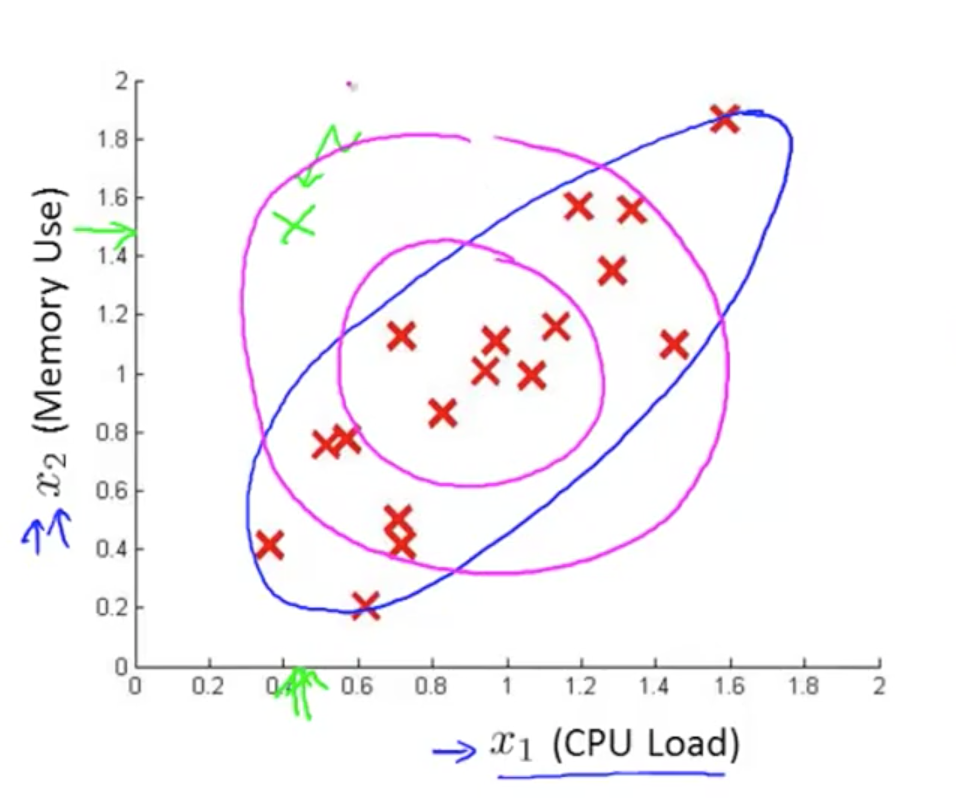
为此，引入了多元高斯分布模型。

定义

多元高斯分布模型被定义为：
$$p(x;\mu ,\Sigma )=\frac{1}{(2\pi {)}^{\frac{n}{2}}|\Sigma {|}^{\frac{1}{2}}}exp(-\frac{1}{2}(x-\mu {)}^T{\Sigma }^{-1}(x-\mu ))$$

其中， $\mu$ 表示样本均值， $\Sigma$ 表示样本协方差矩阵。

多元高斯分布模型的热力图如下：

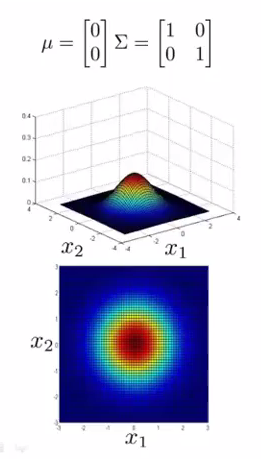
参数

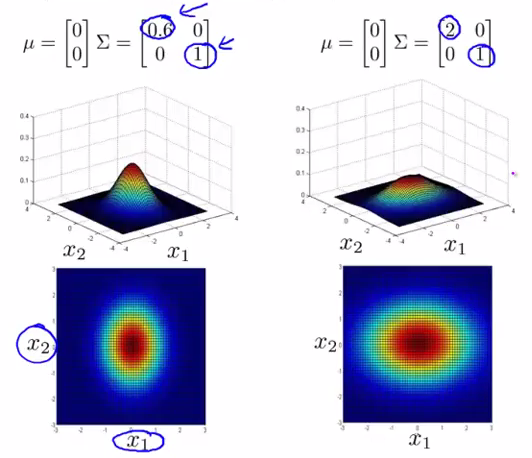
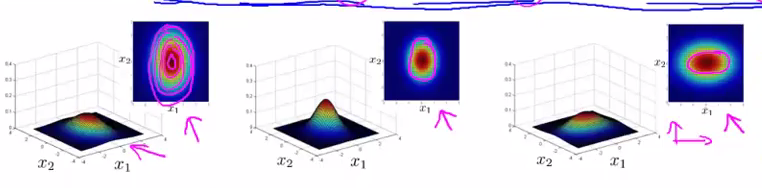
• 改变 $\Sigma$ 主对角线的数值可以进行不同方向的宽度拉伸：
  
• 改变 $\Sigma$ 次对角线的数值可以旋转分布图像：
  
  
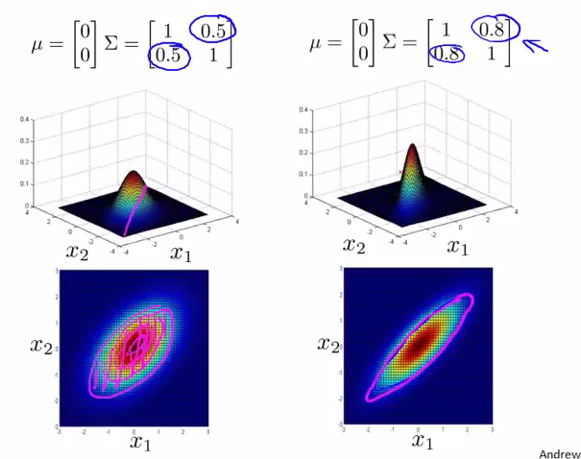
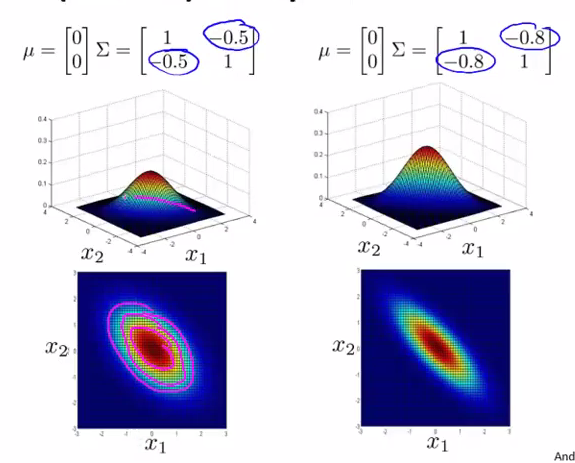
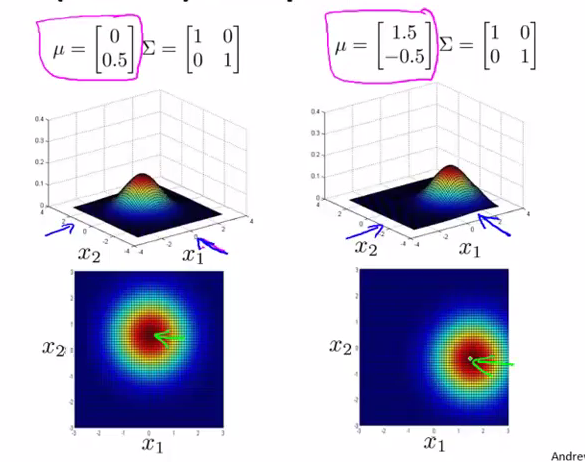
• 改变 $\mu$ 可以对分布图像进行位移：
  

参数估计

多元高斯分布模型的参数估计如下：
$$\mu =\frac{1}{m}\sum _{i=1}^m{x}^{(i)}$$$$\Sigma =\frac{1}{m}\sum _{i=1}^m(x^{(i)}-\mu )(x^{(i)}-\mu {)}^T$$

算法流程

采用了多元高斯分布的异常检测算法流程如下：

1. 选择一些足够反映异常样本的特征 $x_j$ 。

2. 对各个样本进行参数估计：
   $$\mu =\frac{1}{m}\sum _{i=1}^m{x}^{(i)}$$$$\Sigma =\frac{1}{m}\sum _{i=1}^m(x^{(i)}-\mu )(x^{(i)}-\mu {)}^T$$

3. 当新的样本 $x$ 到来时，计算 $p(x)$ ：
   $$p(x)=\frac{1}{(2\pi {)}^{\frac{n}{2}}|\Sigma {|}^{\frac{1}{2}}}exp(-\frac{1}{2}(x-\mu {)}^T{\Sigma }^{-1}(x-\mu ))$$

如果 $p(x)<ϵ$ ，则认为样本 $x$ 是异常样本。

多元高斯分布模型与一般高斯分布模型的差异

实际上，一般的高斯分布模型只是多元高斯分布模型的一个约束，它将多元高斯分布的等高线约束到了如下所示同轴分布（概率密度的等高线是沿着轴向的）：

由此可以看出，基于多元高斯分布模型的异常检测应用十分有限。

最后

以上就是怡然飞鸟为你收集整理的8.6 多元高斯分布模型-机器学习笔记-斯坦福吴恩达教授多元高斯分布模型的全部内容，希望文章能够帮你解决8.6 多元高斯分布模型-机器学习笔记-斯坦福吴恩达教授多元高斯分布模型所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。