如何用Green定理求五星形曲线所围面积的"精确解"

问题

这条曲线是跟着别人玩Geogebra，演示圆圆相切并滚动情况下内摆线轨迹的时候，我突发奇想调整参数凑出来的，感觉它跟五角星最接近、参数方程也简洁，用来做例子很理想。

曲线的参数方程:

$$begin{cases} x &= -9 sin (2 t)-5 sin (3 t) \[6pt] y & = 9 cos (2 t)-5 cos (3 t) end{cases}quad tin[0,2pi]$$
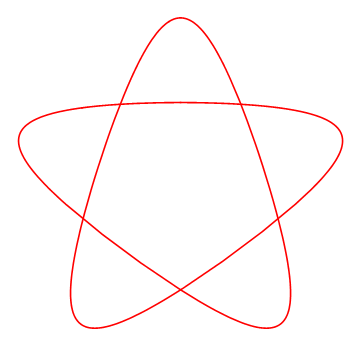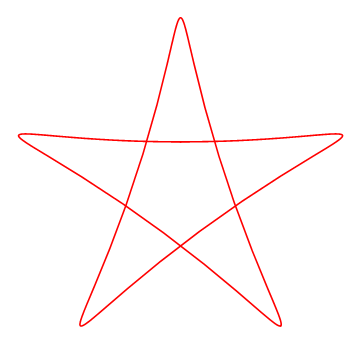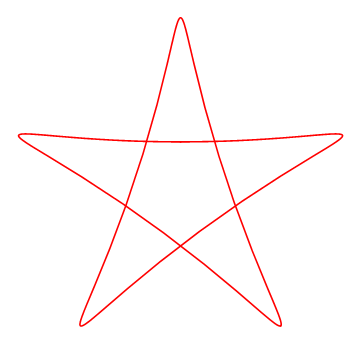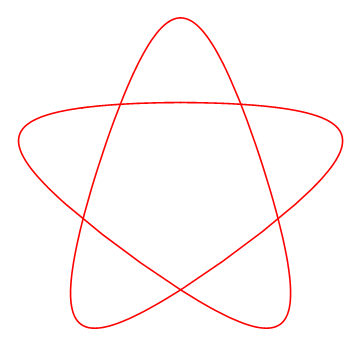
曲线形如：

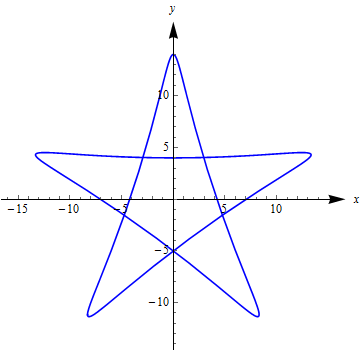
它的隐函数方程也计算过了：

$$begin{array}{rl} F(x,y)=&625(x^2+y^2)^3-36450y(5x^4-10x^2y^2+y^4)\ &+585816(x^2+y^2)^2-41620992(x^2+y^2)+550731776=0 end{array}$$

得到曲线的时候所用的参数动态调整序列图之一：

一直让我困惑的 问题 是：

求该曲线包围的封闭区域面积的解析解

解答

经过一番折腾和取经，终于得到了肯定的答案。
问题的关键是求曲线自交点对应位置的解析解。用到了以下特殊的结果:

1. 观察到曲线最高点坐标 $(0,14)$ 对应于 $t=pi$;
2. 由对称性，当两个点同时从 $t=pi$ 的最高点出发,以相同的速度相背而行, 当 $xleft(pi+Delta tright)=xleft(pi-Delta tright)$ 时恰好是曲线的一个对称交点,而且这个 $Delta t$ 居然可以用 Mathematica 的 Solve 函数解出来! 如下图所示
   
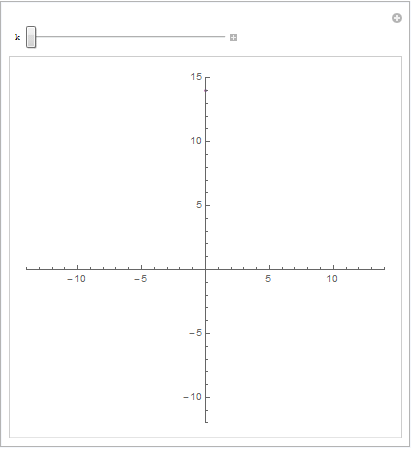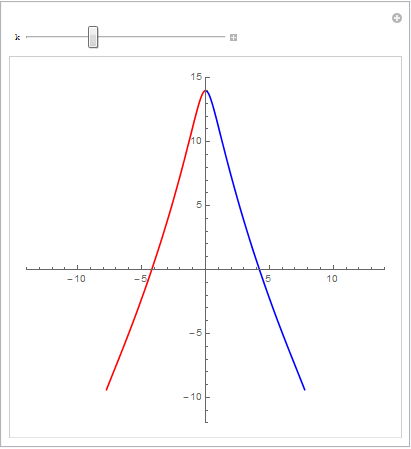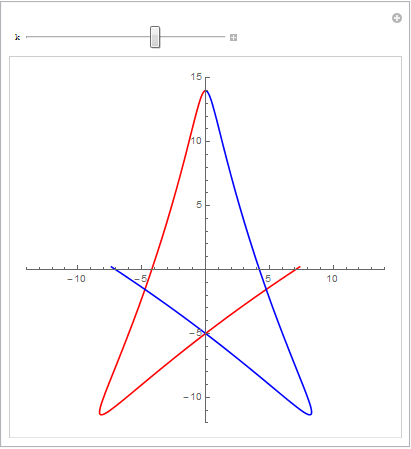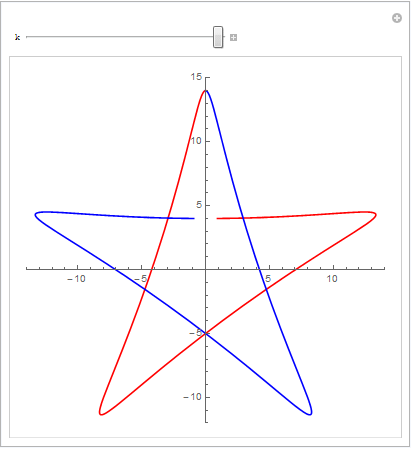
3. 从求出的”交点”再到下一个曲线自己的交点的距离恰好是 $dfrac{2pi}{5}$;
4. 从而曲线所包围的面积的 $dfrac{1}{5}$ 就可以界定出来了! 如图:

ClearAll["Global`*"];
curve={-9Sin[2t]-5Sin[3t],9Cos[2t]-5Cos[3t]};
x[t_]:=Evaluate@curve[[1]]
y[t_]:=Evaluate@curve[[2]]
deltaT=t/.Solve[{x[[Pi]+t]-x[[Pi]-t]==0,0<t<Pi},t]/.C[1]->0;
t0=%[[1]]-2 [Pi]/5//Simplify;
ParametricPlot[curve u,{t,0,2Pi},{u,0,1},MeshFunctions->{Boole[((Pi-t0<=#3<=Pi+t0)&&(0<=#4<=1))]&},Mesh->{{.2}},MeshShading->{{None},{Red}},PlotPoints->150,Axes->True,AxesOrigin->{0,0},Frame->False,AxesStyle->Directive[Black,12,Arrowheads[.035],FontFamily->"Arial"],PlotRangePadding->Scaled[.1],Ticks->Automatic]/.Line[x_]:>{Blue,Line[x]}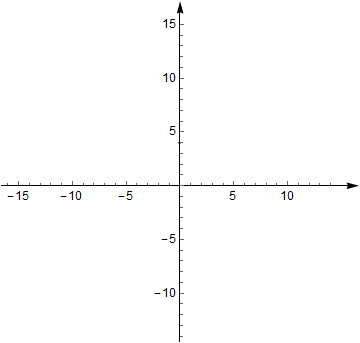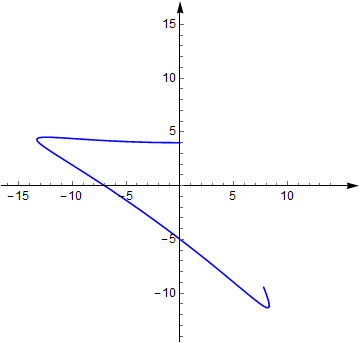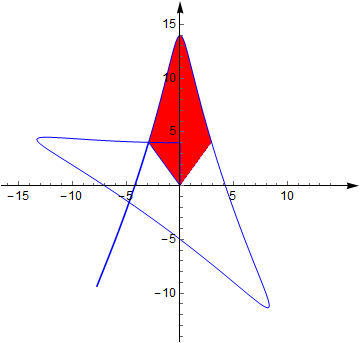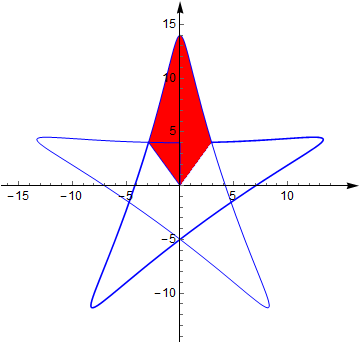

ClearAll["Global`*"];
curve={-9Sin[2t]-5Sin[3t],9Cos[2t]-5Cos[3t]};
x[t_]:=Evaluate@curve[[1]]
y[t_]:=Evaluate@curve[[2]]
Solve[x[[Pi]+t]-x[[Pi]-t]==0,t]/.C[1]->0;
t0=%[[4,1,2]]-2 [Pi]/5//FullSimplify;
ParametricPlot[curve u,{t,0,2Pi},{u,0,1},MeshFunctions->{Boole@( ( Or[(Pi-t0)<=  #3<= (Pi+t0),(7Pi/5-t0)<=  #3<= (7Pi/5+t0)] )&&0<= #4<=1)&},Mesh->{{.2}},MeshShading->{{Green},{Red}},PlotPoints->90,Axes->False]/.Line[_]:>Sequence[]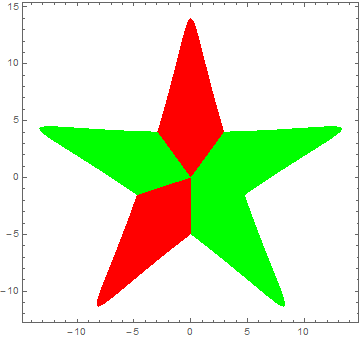

5. 对这个区域使用Green定理, 两条直线段边界都在过原点的直线上,选择恰当的公式可以简化处理。
6. 从而，最后得到的面积是:

$$A=261 pi-frac{252}{625} sqrt{3 left(5154 sqrt{181}-68561right)} -435 text{ arcctg}left(sqrt{frac{1}{33} left(6 sqrt{181}-79right)}right)$$

等价的解析表达形式还可能有其它，但是这已经不重要了。近似解：

214.8531269265365455525903613514926575559640647492478893827700660624406115425295897791820009518934877062772137299324370327089756015443937609267786516798106670343055981006246566712290619761054779907606252474143374263340754820953717866626420862990504583……

附录

顺便,发现五角星可以这样画了

ClearAll["Global`*"];
curve={-9Sin[2t]-5Sin[3t],9Cos[2t]-5Cos[3t]};
x[t_]:=Evaluate@curve[[1]]
y[t_]:=Evaluate@curve[[2]]
deltaT=t/.Solve[{x[[Pi]+t]-x[[Pi]-t]==0,0<t<Pi},t];
t0=deltaT[[1]]-2 [Pi]/5//Simplify;
ParametricPlot[curve u,{t,0,2Pi},{u,0,1},MeshFunctions->{Boole@( ( Or[Pi/5<=  #3<= (Pi/5+t0),3Pi/5<=  #3<= (3Pi/5+t0),Pi<=  #3<= (Pi+t0),7Pi/5<=  #3<= (7Pi/5+t0),9Pi/5<=  #3<= (9Pi/5+t0)] )&&0<= #4<=1)&},Mesh->{{.2}},MeshShading->{{Yellow},{Red}},PlotPoints->120,Axes->False]/.Line[_]:>Sequence[]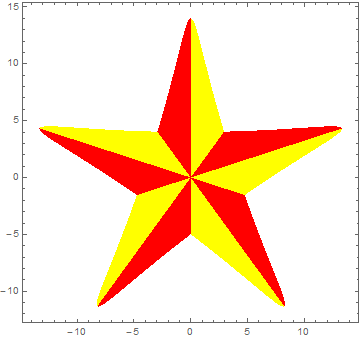

最后

以上就是俊秀西牛为你收集整理的如何用Green定理求五星形曲线所围面积的"精确解"的全部内容，希望文章能够帮你解决如何用Green定理求五星形曲线所围面积的"精确解"所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。