数据结构 — AVL tree（平衡二叉树）

69 阅读 0 评论 46 点赞

我是靠谱客的博主俭朴学姐，最近开发中收集的这篇文章主要介绍数据结构 — AVL tree（平衡二叉树），觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

# BST（二叉搜索树、二叉查找树、二叉排序树）

定义：

1、要么是一棵空树

2、如果不为空，那么其左子树节点的值都小于根节点的值；右子树节点的值都大于根节点的值

3、其左右子树也是二叉搜索树

# AVL tree（平衡二叉树）

定义：

平衡二叉树（Balanced Binary Tree）又被称为AVL树（有别于AVL算法），且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。平衡二叉树的常用算法有红黑树、AVL、Treap、伸展树等。

最小不平衡子树：以离插入结点最近、且平衡因子绝对值大于 1 的结点作根结点的子树。

调整该子树的分为四种情况：

（1）LL形

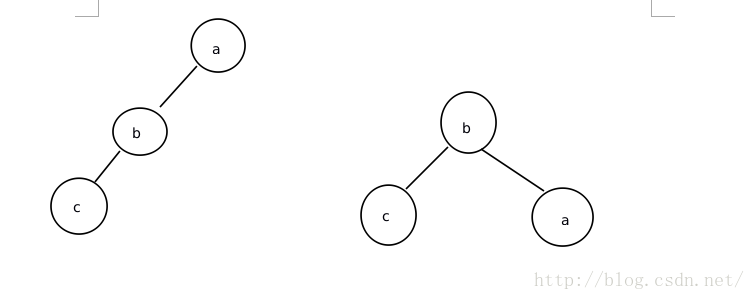
（2）LR形

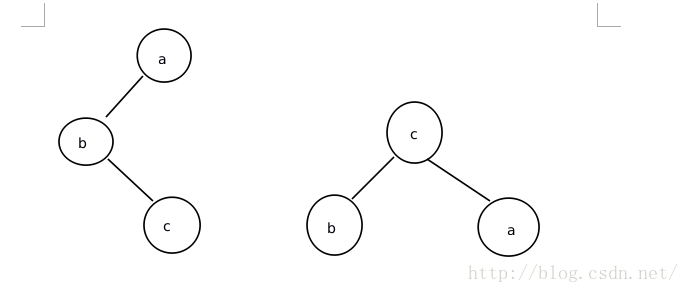
（3）RR形

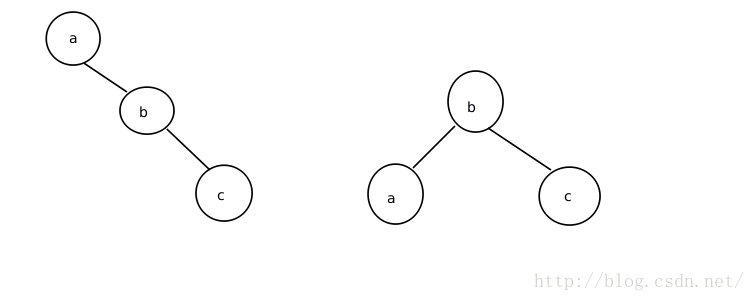
（4）RL形

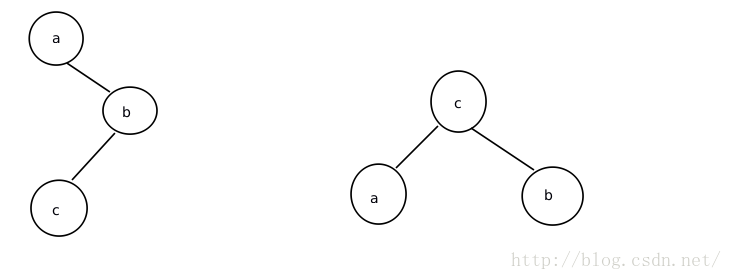
代码实现：

LR：

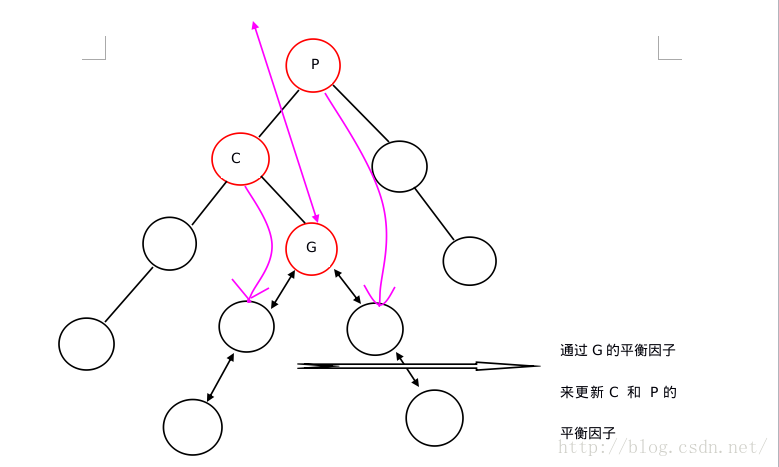
RL：

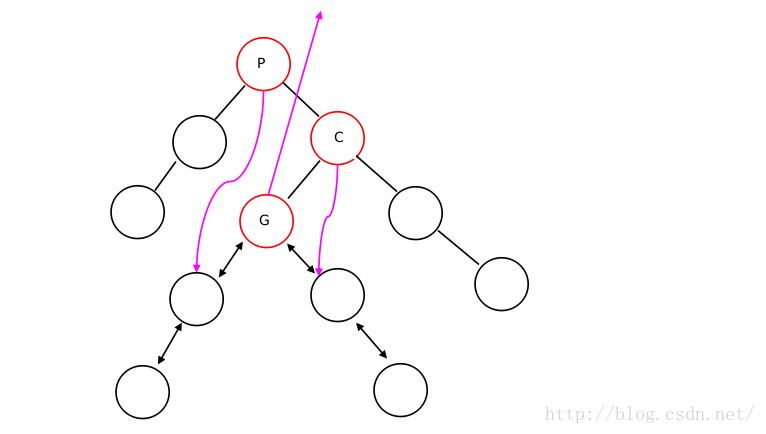
#include<stdio.h>
#include<iostream>
using namespace std;

#define FALSE 0
#define TRUE 1

typedef struct {
    int key;
} element;

typedef struct tree_node {
    struct tree_node *left_child;
    element data;
    short bf;
    struct tree_node *right_child;
} tree_node, *tree_pointer;

int unbalanced = FALSE;
tree_pointer root = NULL;

void left_rotation(tree_pointer *parent, int *unbalanced);
void right_rotation(tree_pointer *parent, int *unbalanced);
void avl_insert(tree_pointer *parent, element x, int *unbalanced);
/*
 *1.如果要插入的元素的父节点为空则为其分配内存并处理
 *2.如果小于父节点的数据域则插入父节点的左孩子，并旋转
 *3.如果大于父节点的数据域则插入父节点的右孩子，并旋转
 */
void avl_insert(tree_pointer *parent, element x, int *unbalanced) {
    if(!*parent) {
        *unbalanced = TRUE;
        *parent = new tree_node();
        (*parent)->left_child = (*parent)->right_child = NULL;
        (*parent)->bf = 0;
        (*parent)->data = x;
    }
    else if(x.key < (*parent)->data.key) {
        avl_insert(&(*parent)->left_child, x, unbalanced);
        if(*unbalanced) {
            /*
             * unbalanced表示是插完之后就不平衡了 和 判断还用不用处理平衡因子
             */
            switch((*parent)->bf) {
                case -1:
                    (*parent)->bf = 0;
                    *unbalanced = FALSE;
                    break;
                case 0:
                    (*parent)->bf = 1;
                    break;
                case 1:
                    left_rotation(parent,unbalanced);
            }
        }
    }
    else if(x.key > (*parent)->data.key) {
        avl_insert(&(*parent)->right_child, x, unbalanced);
        if(*unbalanced) {
            switch((*parent)->bf) {
                case 1:
                    (*parent)->bf = 0;
                    *unbalanced = FALSE;
                    break;
                case 0:
                    (*parent)->bf = 1;
                    break;
                case -1:
                    right_rotation(parent, unbalanced);
            }
        }
    }
    else {
        *unbalanced = FALSE;
        printf("该元素已经存在！n");
    }
}

void left_rotation(tree_pointer *parent, int *unbalanced) {
   tree_pointer grand_child, child;
    child = (*parent)->left_child;
    if(child->bf == 1) {
        //LL
        (*parent)->left_child = child->right_child;
        child->right_child = *parent;
        (*parent)->bf = 0;
        (*parent) = child;
    } else {
        //LR
        grand_child = child->right_child;
        child->right_child = grand_child->left_child;
        grand_child->left_child = child;
        (*parent)->left_child = grand_child->right_child;
        grand_child->right_child = (*parent);
        switch(grand_child->bf) {
            case 1:
                (*parent)->bf = -1;
                child->bf = 0;
            case 0:
                (*parent)->bf = child->bf = 0;
            case -1:
                (*parent)->bf = 0;
                child->bf = 1;
        }
        (*parent) = grand_child;
    }
    (*parent)->bf = 0;
    *unbalanced = FALSE;
}

void right_rotation(tree_pointer *parent, int *unbalanced) {
    tree_pointer grand_child, child;
    child = (*parent)->right_child;
    if(child->bf == -1) {
        //RR
        (*parent)->right_child = child->left_child;
        child->left_child = (*parent);
        (*parent) = child;
    } else {
        //RL
        grand_child = child->left_child;

        child->left_child = grand_child->right_child;
        grand_child->right_child = child;
        (*parent)->right_child = grand_child->left_child;
        grand_child->left_child = (*parent);
        switch(grand_child->bf) {
            case 1:
                (*parent)->bf = 0;
                child->bf = -1;
            case 0:
                (*parent)->bf = child->bf = 0;
            case -1:
                (*parent)->bf = 1;
                child->bf = 0;
        }
        (*parent) = grand_child;
    }
    (*parent)->bf = 0;
    *unbalanced = FALSE;
}
void raverse(tree_pointer root) {
    if(root) {
        printf("%d ",root->data.key);
        raverse(root->left_child);
        raverse(root->right_child);
    }
}
int main() {
    int arr[11] = {15,6,18,3,7,17,20,2,4,13,9};
    element arr_x[11];
    for(int i = 0; i<11; i++) {
    
        arr_x[i].key = arr[i];
     //   cout<<arr_x[i].key<<endl;
        avl_insert(&root, arr_x[i], &unbalanced);
    }
    
    raverse(root);
    printf("n");
    return 0;
}