概述
◆前言
小编重点在这里为大家讲解一下二叉树的性质，一共有五点，理论与实践相结合，愿能为大家提供帮助。
◆定义
二叉树：
n(n>=0)个元素的有限集合，该集合或者为空，或者由一个根及两棵互不相干的左子树和右子树组成，其中左子树和右子树也均为二叉树。
满二叉树：
深度为k（k≥1）的二叉树且有（2^i）-1个结点的二叉树
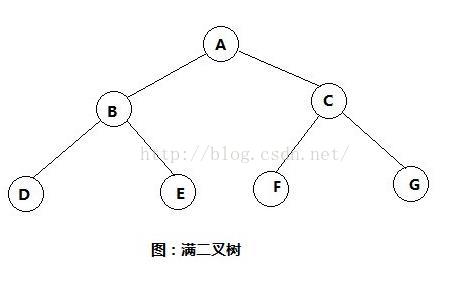
完全二叉树：
如果对满二叉树按从上到下，从左到右的顺序编号，并在最下一层删去部分结点（删去最后一层仍有结点），如果删除的这些结点的 编号是连续的且删除的结点中含有最大编号的结点，则此二叉树为完全二叉树
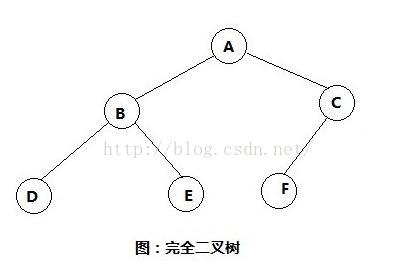
完全二叉树是由满二叉树演化而来
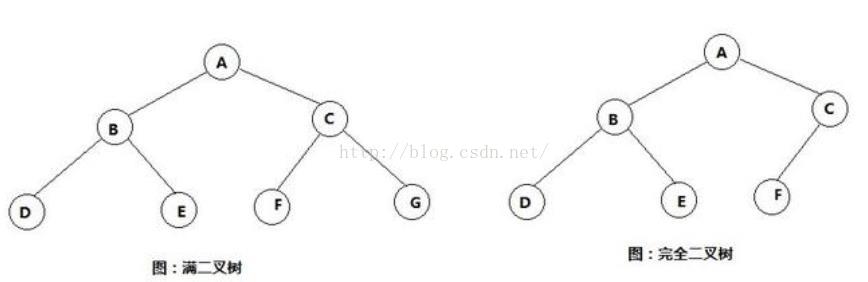
◆性质
★性质一
二叉树第I（I≥1）层上至多有2^(i-1)个结点
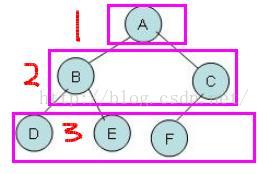
图（1）
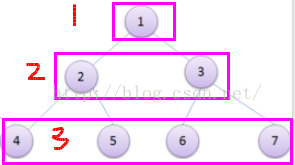
图（2）
解说：
图（1）与图（二）均为二叉树，图（1）为一般二叉树，根据性质可知，第三层，理论上结点个数为2^(i-1)=2^(3-1)=4，实际第三层结点个数为3；图（2）为满二叉树，满二叉树的结点数为二叉树可以容纳的最大值，继而，第三层，理论：2^(i-1)=2^(3-1)=4；实际：2^(i-1)=2^(3-1)=4。即可证明此理论的正确性
★性质二
深度为k（k≥1）的二叉树至多有（2^i）-1个结点
图（1）
图（2）
解说：
图（1）与图（2）均为二叉树，图（1）为一般二叉树，根据性质可知，深度为3，理论上结点个数为（2^i）-1=（2^3）-1=8;实际上结点个数为6；图（2）为满二叉树，满二叉树的结点数为二叉树可以容纳的最大值，继而，深度为3，结点个数为（2^i）-1=（2^3）-1=8，实际与理论一一致。
真题：
一颗深度为6的满二叉树有（）
√Α.63个结点 Β.64个结点
C.127个结点 D.128个结点
深度为k（k≥1）的二叉树至多有（）个结点
A. 2^k √B. 2^k -1
c.2^(k-1) D.2^k +1
★性质三
对任何一颗二叉树，若度数为0的结点（叶结点）个数为n0，度数为2的结点个数为n2，则n0=n2+1
真题：
一颗二叉树T，度为2的结点数为20个，则叶子结点数为（）
A.19个 B.10个
√C.21个 D.22个
对任何一棵二叉树T，若叶结点数为5个，则度为2的结点个数为（）
√A.4 B.5
C.6 D.无法确定
★性质四
含有n个结点的完全二叉树的深度为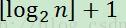
在所做题目当中，还未涉及到此性质的考查，继而值得关注
★性质五
如果将一棵有n个结点的完全二叉树按层编号：将一棵二叉树中的所有n个结点按从第一层到最大层，每层从左到右的顺序依次标记为1，2……，n.则对任一编号为i（n≥i≥1）的结点A有：
①若i=1，则结点A是根；若i>1，则A的双亲Parent（A）的编号为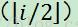
②若2*i>n，则结点A既无左孩子，又无右孩子；否则A的左孩子Lchild（X）的编号为2*i
③若2*i+1>n，则结点A无右孩子，否则，A的右孩子Rchild（A）的编号为2*i+1
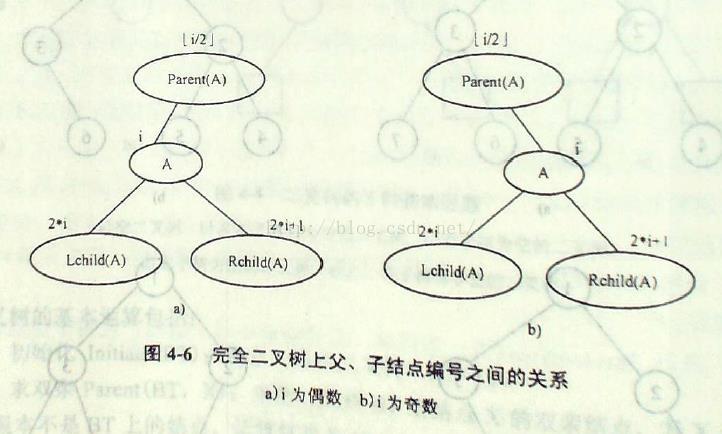
真题：
一棵具有n个结点的完全二叉树中，从树根起，自上而下、自左至右给所有结点编号，设根结点编号为1，若编号为i的结点有父结点，那么其父结点的编号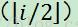
◆总结
二叉树的性质共有五点，考查频率最高的是前三点，出题的方式有两种：（1）直接考定义 （2）给具体数值，求具体数值。其中第四点和第五点值得大家在这次考试学习过程中值得关注，因为从真题来看，知识点是固定的，然而题目基本是不重复的。大家要注意哦
最后
以上就是单纯春天为你收集整理的《数据结构导论之二叉树》◆前言◆定义◆性质◆总结的全部内容，希望文章能够帮你解决《数据结构导论之二叉树》◆前言◆定义◆性质◆总结所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复