线性回归（两种方式代码实现）

81 阅读 0 评论 54 点赞

我是靠谱客的博主忧郁翅膀，最近开发中收集的这篇文章主要介绍线性回归（两种方式代码实现），觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

方式一：最小二乘法（正规方程）

公式推导
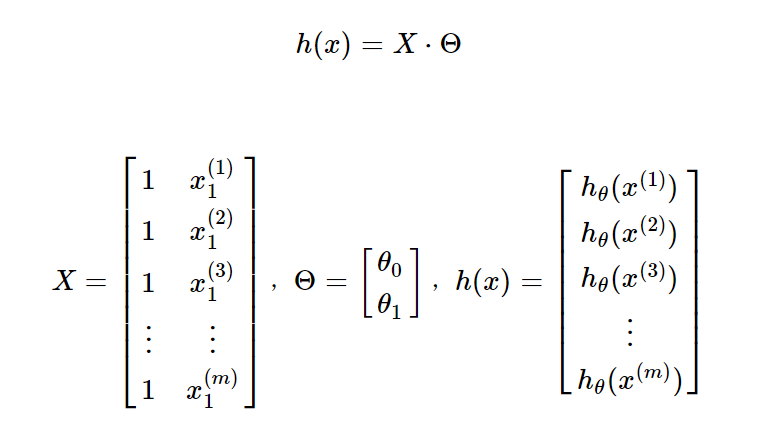
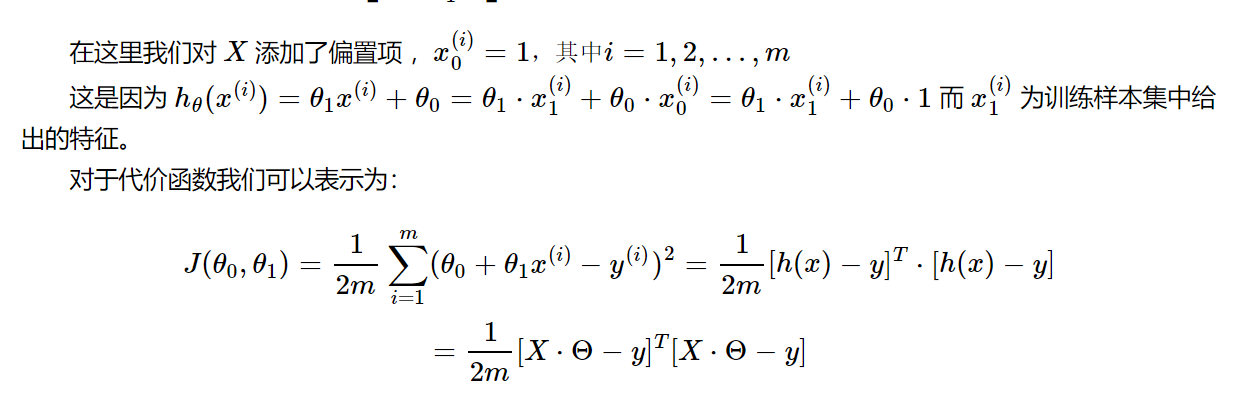
在这里插入图片描述

其中：

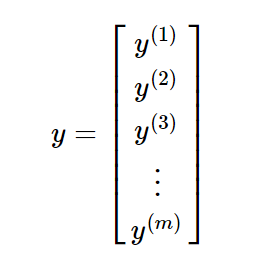
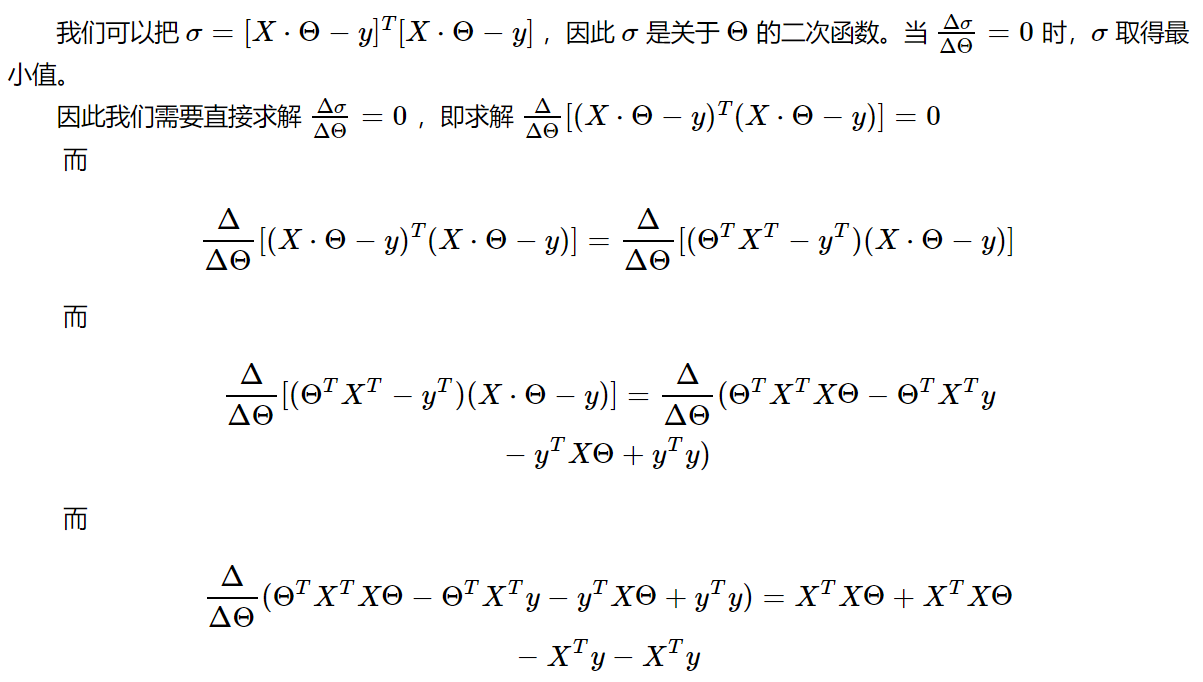
代码实现：
1.导入库

import numpy as np
from sklearn.datasets import load_boston

boston = load_boston()
x = boston.data
y = boston.target

2.由于我们的特征中没有1，所以需要插入1
然后我们需要把1和特征放在一起

X_b = np.hstack([np.ones((len(x),1)),x]

3.用正规方程求解参数

theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)

4.获得截距（b）和系数(w)

intercept = theta[0]
coef = theta[1:]

5.预测

x_test = x[0].reshape(1,-1)
x_test = np.hstack([np.ones((len(x_test),1)),x_test])
x_test.dot(theta) #预测结果

6.封装代码

import numpy as np
class LinearRegression_2:
    def __init__(self):
        self._theta = None
        self.intercept_ = None
        self.coef_ = None
    
    def fit(self,x_train,y_train):
        X_b = np.hstack([np.ones((len(x_train),1)), x_train])
        self._theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train)
        self.intercept_ = self._theta[0]
        self.coef_ = self._theta[1:]
        
        return self
    
    def predict(self,x_predict):
        X_b = np.hstack([np.ones((len(x_predict),1)), x_predict])
        return X_b.dot(self._theta)
    
    def __repr__(self): #用作自我介绍
        return "LinearRegression_2()"

此代码在矩阵不可逆时，容易报错

方式二：梯度下降

损失函数：
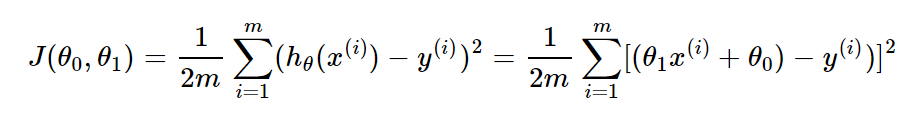
在这里插入图片描述
单元线性回归

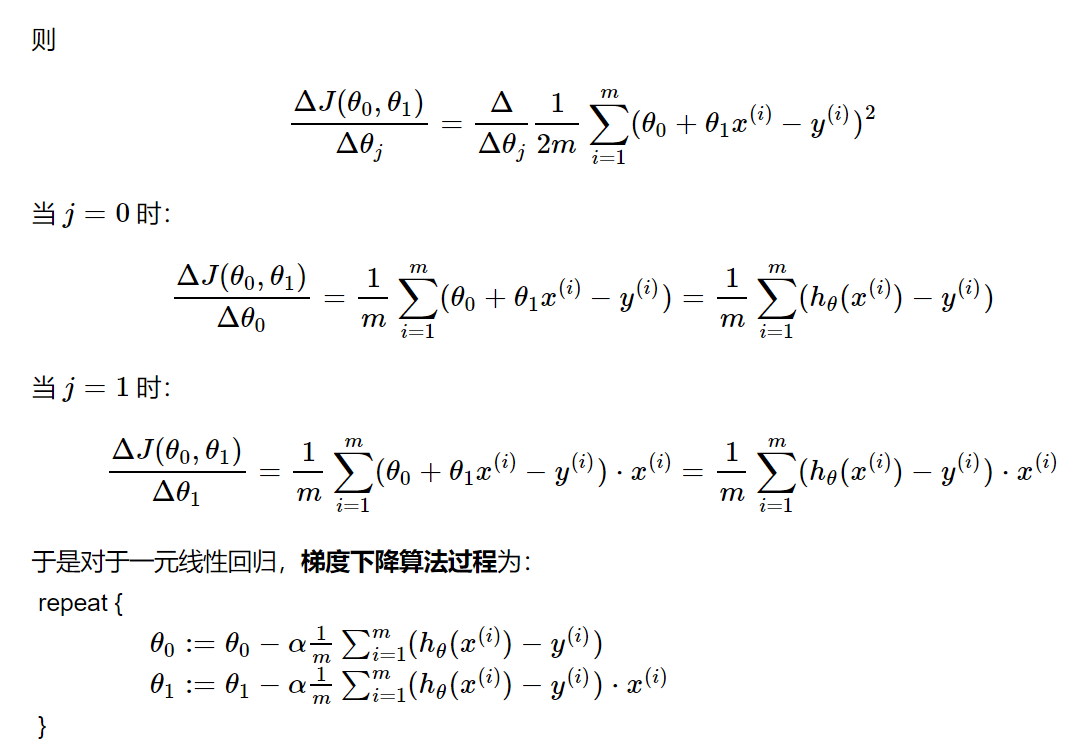
同理可得多元线性回归

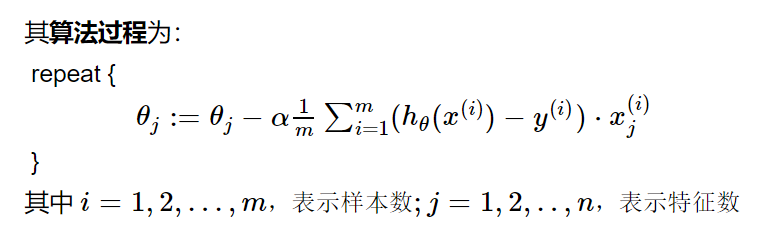
代码`

class LinerRegression2(object):
    def __init__(self,learning_rate=0.01, max_iter=100, seed=None):
         np.random.seed(seed)
         self.lr = learning_rate #设置学习率
         self.max_iter = max_iter
         self.loss_arr = []

    def fit(self,x,y):
        self.x = x
        self.x_b = np.hstack([np.ones((len(x), 1)), x])
        self.x_b_dim = np.size(self.x_b,1)
        self.x_sample = np.size(self.x_b, 0)
        self.y = y
        self.w = np.random.normal(1,0.001,(self.x_b_dim,1))
        for i in range(self.max_iter):
            self._train_step()
            self.loss_arr.append(self.loss())

    def _f(self,x,w):
        return x.dot(w)

    def predict(self,x=None):
        if x is None:
            x = self.x_b
        y_pred = self._f(x,self.w)
        return y_pred

    def loss(self,y_true=None,y_pred=None):
        if y_true is None or y_pred is None:
            y_true = self.y
            # y_pred = self.predict(self.x_b)
        return np.sum(np.power(y_true-self.x_b.dot(self.w),2))/self.x_sample

    def _calc_gradient(self):
        d_w = np.empty(self.x_b_dim).reshape(-1,1)
        d_w[0] = np.sum(self.x_b.dot(self.w)-self.y)
        for i in range(1,self.x_b_dim):
            print(self.x_b.shape)
            print(self.w.shape)
            print(self.y.shape)
            print(self.x_b[:,i].T.shape)
            d_w[i] = np.squeeze((self.x_b.dot(self.w)-self.y)).dot(self.x_b[:,i].T)
        return d_w*2/self.x_sample

    def _train_step(self):
        d_w = self._calc_gradient()
        self.w = self.w-self.lr*d_w
        return  self.w

注意：请将输入数据进行归一化，否则梯度下降的时候，可能数据可能会非常大，最终溢出