机器学习+周志华+第五章习题+解决异或问题的单层RBF神经网络

45 阅读 0 评论 30 点赞

我是靠谱客的博主贪玩水壶，最近开发中收集的这篇文章主要介绍机器学习+周志华+第五章习题+解决异或问题的单层RBF神经网络，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

5.7根据式（5.18）和（5.19），试构造一个能解决异或问题的单层RBF神经网络。

RBF(Radial Basis Function,径向基函数)网络，是一种单隐层前馈神经网络，它使用径向基函数作为隐层神经元激活函数，而输出层则是对隐层神经元输出的线性组合。

RBF隐层相当于把输入映射到一个更高维空间，使得不可分的数据线性可分。

对于异或问题，构造数据:

异或真值表
X1	X2	X3
0	0	0
0	1	1
1	0	1
1	1	0

设计RBF网：

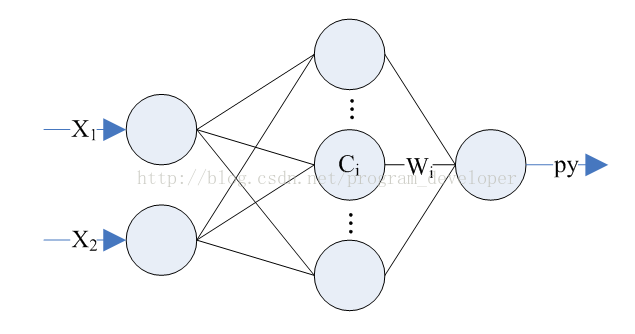
（1）输入层：由于有2个输入，所以输入层2个神经元

（2）隐层：隐层神经元越多拟合的越好，这里我设置十个隐层神经元。

（3）输出层：1个神经元。

该网络参数有：

（1）Wi：隐层第i个神经元与输出神经元的权值。

（2）Ci：隐层第i个神经元的中心

（3） βi：样本与第i个神经元的中心的距离的缩放系数

两步训练RBF网络：

（1）确定Ci常用的方法有：随机采样、聚类等。、

（2）利用ABP算法来确定参数Wi和βi。

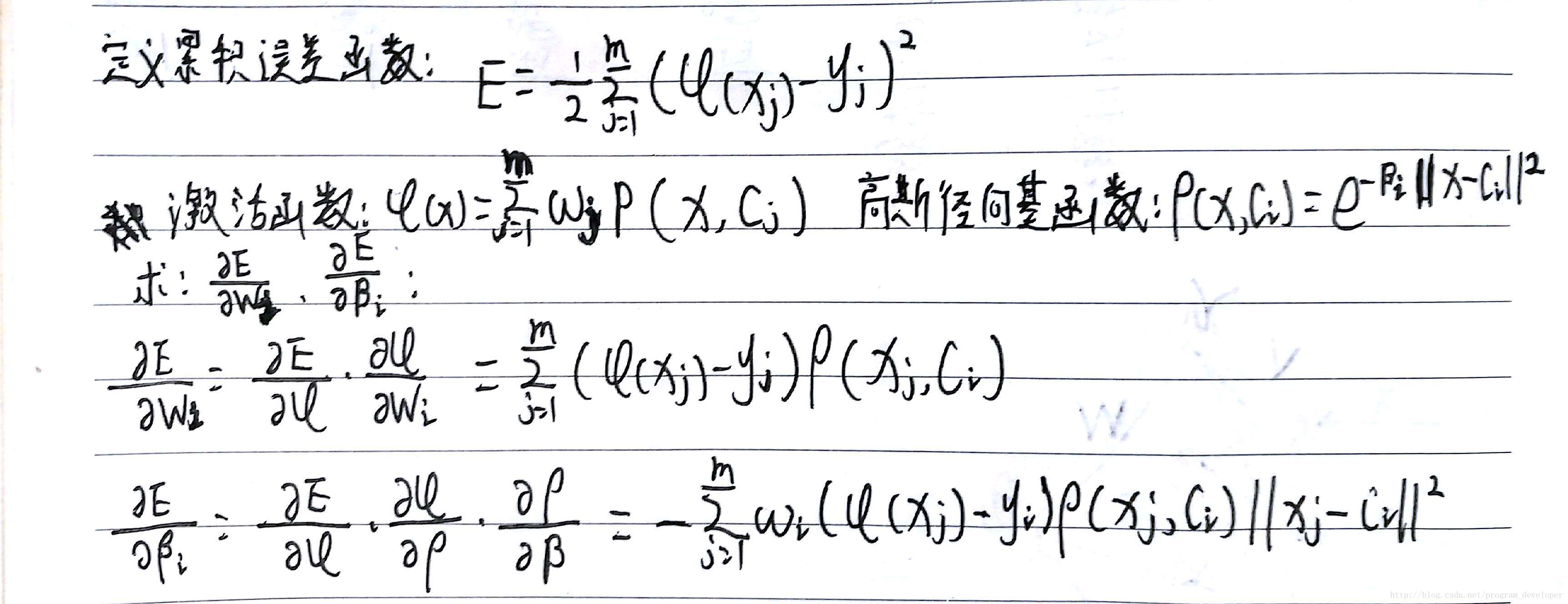
在代码中令学习率： η=0.5

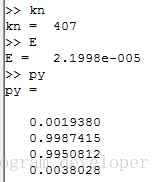
kn是指：迭代了407次。

E是指：累积误差。

py是指：真是的预测输出，即输出层的输出。

RBF网络的MATLAB代码为：

clear
x=[0 0;0 1; 1 0;1 1];
y=[0;1;1;0];

hideNum=10;               %隐层神经元数目，要求必须大于输入层个数
rho=rand(4,hideNum);       %径向基函数的值
py=rand(4,1);             %输出值
w=rand(1,hideNum);        %隐层第i个神经元与输出神经元的权值
beta=rand(1,hideNum);     %样本与第i个神经元的中心的距离的缩放系数
eta=0.5;                    %学习率

c=rand(hideNum,2);     %隐层第i个神经元的中心

kn=0;                 %累计迭代的次数
sn=0;                 %同样的累积误差值累积次数
previous_E=0;          %前一次迭代的累积误差

while(1)
  kn=kn+1;
  E=0;
  %计算每个样本的径向基函数值
  for i=1:4
    for j=1:hideNum
      p(i,j)=exp(-beta(j)*(x(i,:)-c(j,:))*(x(i,:)-c(j,:))');
     end
     py(i)=w*p(i,:)'; 
   end
   %计算累积误差
   for i=1:4
     E=E+((py(i)-y(i))^2);    %计算均方误差
   end
     E=E/2;    %累积误差
   
   %更新w、beta
   delta_w=zeros(1,hideNum);
   delta_beta=zeros(1,hideNum);
   for i=1:4
     for j=1:hideNum
       delta_w(j)=delta_w(j)+(py(i)-y(i))*p(i,j);
       delta_beta(j)= delta_beta(j)-(py(i)-y(i))*w(j)*(x(i,:)-c(j,:))*(x(i,:)-c(j,:))'*p(i,j);
      end
     end
     
    %更新w、beta
    w=w-eta*delta_w/4;
    beta=beta-eta*delta_beta/4;
    
    %迭代终止的条件
    if(abs(previous_E-E)<0.0001)
       sn=sn+1;
       if(sn==50)
         break;
        end
     else
       previous_E=E;
       sn=0;
      end
      
 end

实验的代码下载地址：https://github.com/Microstrong0305/Machine-Learning-ZhouZhiHua