机器学习-降维算法(MDS算法)

一，介绍

在现实数据中，很多数据都是高纬度的，在高纬度情况下进行数据处理将会有极大的数据处理量。为了，减少计算量，常常需要缓解这种数据维度灾难，这有两种途径：降维和特征选择。

我们在这里介绍其中一种降维算法：MDS算法。MDS算法要求原始空间中样本之间的距离在低维空间中得以保持。但是为了有效降维，我们往往只需要降维后的距离与原始空间距离尽可能接近即可。

要学习MDS算法，首先，我们要了解范数的概念：

（1）向量范数

如果定义一个向量为：a=[-5，6，8, -10]

向量的1范数即：向量的各个元素的绝对值之和，上述向量a的1范数结果就是：29；

向量的2范数即：向量的每个元素的平方和再开平方根，上述a的2范数结果就是：15；

向量的负无穷范数即：向量的所有元素的绝对值中最小的：上述向量a的负无穷范数结果就是：5； 
向量的正无穷范数即：向量的所有元素的绝对值中最大的：上述向量a的负无穷范数结果就是：10；

（2）矩阵范数 
定义矩阵A = [ -1  2 -3； 
                        4 -6  6]

矩阵的1范数（也叫A的列范数）即：矩阵的每一列上的元素绝对值先求和，再从中取个最大的，（列和最大），上述矩阵A的1范数先得到[5,8,9]，再取最大的最终结果就是：9；

矩阵的2范数即：矩阵ATA的最大特征值开平方根，A的特征值为[3.06384528e-15,7.50621894e-0.1, 1.01249378e+02]上述矩阵A的2范数得到的最终结果是：10.0623；

矩阵的无穷范数即（也叫A的行范数）：矩阵的每一行上的元素绝对值先求和，再从中取个最大的，（行和最大），上述矩阵A的1范数先得到[6；16]，再取最大的最终结果就是：16；

接下来我们要介绍机器学习的低秩，稀疏等一些地方用到的范数，一般有核范数，L0范数，L1范数（有时很多人也叫1范数，这就让初学者很容易混淆），L21范数（有时也叫2范数），F范数。。。上述范数都是为了解决实际问题中的困难而提出的新的范数定义，不同于前面的矩阵范数。

矩阵的核范数即：矩阵的奇异值（将矩阵svd分解）之和，这个范数可以用来低秩表示（因为最小化核范数，相当于最小化矩阵的秩——低秩），上述矩阵A最终结果就是：10.9287；

矩阵的L0范数即：矩阵的非0元素的个数，通常用它来表示稀疏，L0范数越小0元素越多，也就越稀疏，上述矩阵A最终结果就是：6;

矩阵的L1范数即：矩阵中的每个元素绝对值之和，它是L0范数的最优凸近似，因此它也可以表示稀疏，上述矩阵A最终结果就是：22;

矩阵的F范数即：矩阵的各个元素平方之和再开平方根，它通常也叫做矩阵的L2范数，它的有点在它是一个凸函数，可以求导求解，易于计算，上述矩阵A最终结果就是：10.0995;

矩阵的L21范数即：矩阵先以每一列为单位，求每一列的F范数（也可认为是向量的2范数），然后再将得到的结果求L1范数（也可认为是向量的1范数），很容易看出它是介于L1和L2之间的一种范数，上述矩阵A最终结果就是：17.1559。

算法推导：

假定m个样本之间的距离在原始控件的距离矩阵为D，我们目的是获得降维到d维度的样本矩阵Z：

即，第i个样本和第j个样本在D中距离为dist[i,j]，在Z中为||Zi-Zj||（矩阵第i行减去第j行后的1范数），且dist[i,j]=||Zi-Zj||

我们令，则，从而得到：

                            （1）

为了便于讨论，我们令样本矩阵Z被中心化，即：

我们可以得到：

                             （2）

我们令：

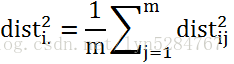
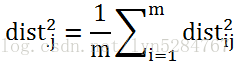
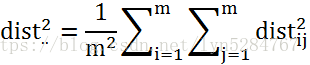                                                         （3）

（2）（3）代入（1）可得：

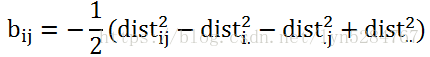
对距离矩阵B做特征值分解，则可以获得Z表达式：

二，代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
import numpy
from sklearn import metrics, datasets, manifold
from scipy import optimize
from matplotlib import pyplot
import pandas
import collections

def calculate_distance(x, y):
    d = numpy.sqrt(numpy.sum((x - y) ** 2))
    return d

# 计算矩阵各行之间的欧式距离；x矩阵的第i行与y矩阵的第0-j行继续欧式距离计算，构成新矩阵第i行[i0、i1...ij]
def calculate_distance_matrix(x, y):
    d = metrics.pairwise_distances(x, y)
    return d


def cal_B(D):
    (n1, n2) = D.shape
    DD = numpy.square(D)                    # 矩阵D 所有元素平方
    Di = numpy.sum(DD, axis=1) / n1         # 计算dist(i.)^2
    Dj = numpy.sum(DD, axis=0) / n1         # 计算dist(.j)^2
    Dij = numpy.sum(DD) / (n1 ** 2)         # 计算dist(ij)^2
    B = numpy.zeros((n1, n1))
    for i in range(n1):
        for j in range(n2):
            B[i, j] = (Dij + DD[i, j] - Di[i] - Dj[j]) / (-2)   # 计算b(ij)
    return B


def MDS(data, n=2):
    D = calculate_distance_matrix(data, data)
    print(D)
    B = cal_B(D)
    Be, Bv = numpy.linalg.eigh(B)             # Be矩阵B的特征值，Bv归一化的特征向量
    # print numpy.sum(B-numpy.dot(numpy.dot(Bv,numpy.diag(Be)),Bv.T))
    Be_sort = numpy.argsort(-Be)
    Be = Be[Be_sort]                          # 特征值从大到小排序
    Bv = Bv[:, Be_sort]                       # 归一化特征向量
    Bez = numpy.diag(Be[0:n])                 # 前n个特征值对角矩阵
    # print Bez
    Bvz = Bv[:, 0:n]                          # 前n个归一化特征向量
    Z = numpy.dot(numpy.sqrt(Bez), Bvz.T).T
    print(Z)
    return Z

if __name__ == '__main__':
    data = numpy.mat([[3,2,4],[2,0,2],[4,2,4]])
    Z = MDS(data)

得到结果：

原始距离矩阵为：

[[0.         3.         1.        ]
 [3.         0.         3.46410162]
 [1.         3.46410162 0.        ]]

可以，第一个点到第二个点的距离为3，第一个点到第三个点的距离为1，第二个点到第三个点的距离为3.464

降维矩阵：

[[-0.81858227  0.46777341]
 [ 2.13331316 -0.06730921]
 [-1.31473089 -0.4004642 ]]

根据上面的矩阵范数计算公式：

第一个点到第三个点的距离为||Z1-Z2||=2.951，第一个点到第二个点的距离为||Z1-Z3||=0.868，第二个点到第三个点的距离为2.447.

我们的数据从三维降低到了2维

最后

以上就是结实小兔子最近收集整理的关于机器学习-降维算法(MDS算法)的全部内容，更多相关机器学习-降维算法(MDS算法)内容请搜索靠谱客的其他文章。